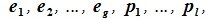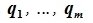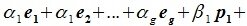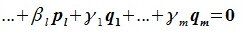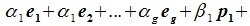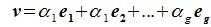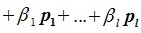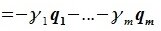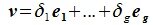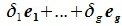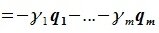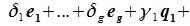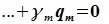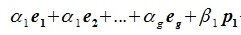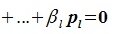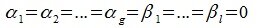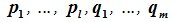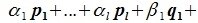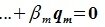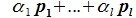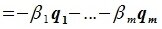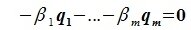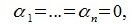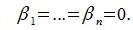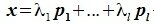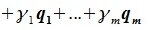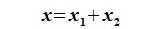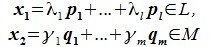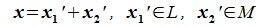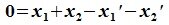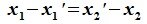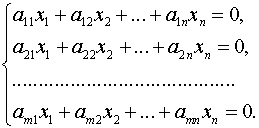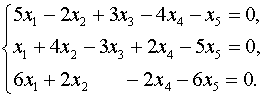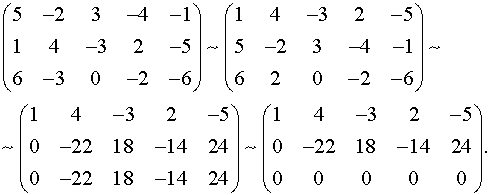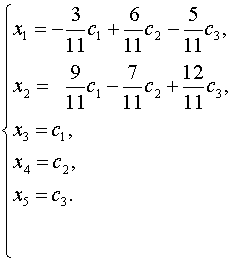В этом разделе вы найдете бесплатные решения задач о линейных пространствах по темам: проверка линейности подпространства, базис пространства и подпространства, ортогональное подпространство, размерность.
Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Решения задач: линейные пространства
Задача 1. Образует ли линейное подпространство пространства $R^4$ множество $V$, заданное по правилу:
Задача 2. Даны векторы $e_1, e_2, e_3, e_4$ и $a$ в стандартном базисе пространства $R^4$.
Требуется:
а) убедиться, что векторы $e_1, e_2, e_3, e_4$ образуют базис пространства $R^4$;
б) найти разложение вектора $a$ по этому базису;
в) найти угол между векторами $e_1$ и $e_2$.
Задача 3.Найти ортогональный базис подпространства $L$, заданного системой уравнений, и базис подпространства $L^$
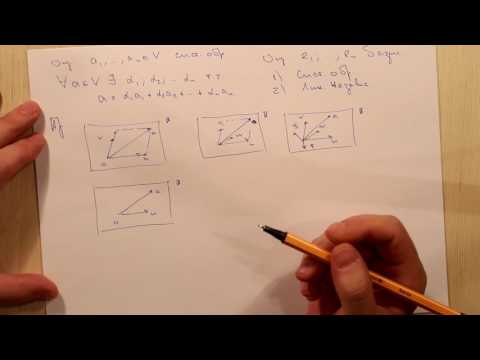
Задача 4. Для каждого из следующих множеств геометрических векторов определить, будет ли это множество линейным подпространством пространства $V_3$ :
1) радиус-векторы точек данной плоскости;
2) векторы, образующие с данным ненулевым вектором $overline$ угол $alpha$;
3) множество векторов, удовлетворяющих условию $|overline|=1$ .
Задача 5. Пусть $L$ — множество многочленов степени не выше 2, удовлетворяющих условию $p(1)+p'(1)+p»(1)=0$. Доказать, что $L$ — линейное подпространство в пространстве $P_2$. Найти его базис и размерность. Дополнить базис подпространства до базиса всего пространства.
Задача 6. Образуют ли многочлены $p_1(x)=x^3+x^2-1$, $p_2(x)=x^2-2x$, $p_3(x)=x^3+x$, $p_4(x)=x^2-3$ базис в пространстве $P_3$?
Задача 7. Доказать, что матрицы вида $$ begin 2a & a+3b-2c\ b & 5c\ end $$ образуют линейное подпространство в пространстве матриц $M_$. Найти его базис и размерность. Дополнить базис подпространства до базиса всего пространства.
Видео:Как разложить вектор по базису - bezbotvyСкачать

Подпространство линейного пространства
Видео:Линейная оболочка. Базис и размерностьСкачать

Определение и размерность подпространства
Определение 6.1. Подпространством L n-мерного пространства R называется множество векторов, образующих линейное пространство по отношению к действиям, которые определены в R.
Другими словами, L называется подпространством пространства R, если из x, y∈L следует, что x+y∈L и если x∈L, то λ x∈L, где λ— любое вещественное число.
Простейшим примером подпространства является нулевое подпространство, т.е. подмножество пространства R, состоящее из единственного нулевого элемента. Подпространством может служить и все пространство R. Эти подпространства называются тривиальными или несобственными.
Подпространство n-мерного пространства конечномерно и его размерность не превосходит n: dim L≤ dim R.
Видео:Образуют ли данные векторы базисСкачать

Сумма и пересечение подпространств
Пусть L и M — два подпространства пространства R.
Cуммой L+M называется множество векторов x+y, где x∈L и y∈M. Очевидно, что любая линейная комбинация векторов из L+M принадлежит L+M, следовательно L+M является подпространством пространства R (может совпадать с пространством R).
Пересечением L∩M подпространств L и M называется множество векторов, принадлежащих одновременно подпространствам L и M (может состоять только из нулевого вектора).
Теорема 6.1. Сумма размерностей произвольных подпространств L и M конечномерного линейного пространства R равна размерности суммы этих подпространств и размерности пересечения этих подпространств:
dim L+dim M=dim(L+M)+dim(L∩M).
Доказательство. Обозначим F=L+M и G=L∩M. Пусть G g-мерное подпространство. Выберем в нем базис 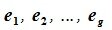
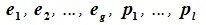
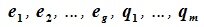
составляют базис F=L+M. Для того, чтобы векторы (6.1) составляли базис пространства F они должны быть линейно независимы и любой вектор пространства F можно представить линейной комбинацией векторов (6.1).
Докажем линейную независимость векторов (6.1). Пусть нулевой вектор пространства F представляется линейной комбинацией векторов (6.1) с некоторыми коэффициентами:
Левая часть (6.3) является вектором подпространства L, а правая часть является вектором подпространства M. Следовательно вектор
принадлежит подпространству G=L∩M. С другой стороны вектор v можно представить линейной комбинацией базисных векторов подпространства G:
Из уравнений (6.4) и (6.5) имеем:
Но векторы 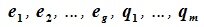
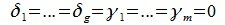
В силу линейной независимости базиса подпространства L имеем:
Так как все коэффициенты в уравнении (6.2) оказались нулевыми, то векторы
линейно независимы. Но любой вектор z из F (по определению суммы подпространств) можно представить суммой x+y, где x∈L, y∈M. В свою очередь x представляется линейной комбинацией векторов 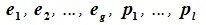
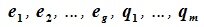
Изучая базисы подпространств L и M и базис подпространства F=L+M (6.10), имеем: dim L=g+l, dim M=g+m, dim (L+M)=g+l+m. Следовательно:
dim L+dim M−dim(L∩M)=dim(L+M). ■
Видео:Базис линейного пространства (01)Скачать

Прямая сумма подпространств
Определение 6.2. Пространство F представляет собой прямую сумму подпространств L и M, если каждый вектор x пространства F может быть единственным способом представлен в виде суммы x=y+z, где y∈ L и z∈M.
Прямая сумма обозначается L⊕M. Говорят, что если F=L⊕M, то F разлагается в прямую сумму своих подпространств L и M.
Теорема 6.2. Для того, чтобы n-мерное пространство R представляло собой прямую сумму подпространств L и M, достаточно, чтобы пересечение L и M содержало только нулевой элемент и чтобы размерность R была равна сумме размерностей подпространств L и M.
Доказательство. Выберем некоторый базис 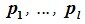
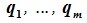
является базисом пространства R. По условию теоремы размерность пространства R n равна сумме подпространств L и M (n=l+m). Достаточно доказать линейную независимость элементов (6.11). Пусть нулевой вектор пространства R представляется линейной комбинацией векторов (6.11) с некоторыми коэффициентами:
Так как левая часть (6.13) является вектором подпространства L, а правая часть — вектором подпространства M и L∩M= 0, то
Но векторы 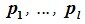
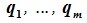
Установили, что (6.12) справедливо лишь при условии (6.15), а это доказывает линейную независимость векторов (6.11). Следовательно они образуют базис в R.
Пусть x∈R. Разложим его по базису (6.11):
Из (6.17) и (6.18) следует, что любой вектор из R можно представить суммой векторов x1∈L и x2∈M. Остается доказать что это представление является единственным. Пусть кроме представления (6.17) есть и следующее представление:
Вычитая (6.19) из (6.17), получим
Так как 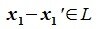
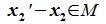
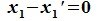
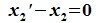
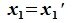
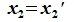
Видео:Базисы суммы и пересечения линейных подпространствСкачать

Решебник.Ру / Кузнецов Л.А. Линейная алгебра. Задача 3
Системы линейных однородных уравнений
Постановка задачи. Найти какой-нибудь базис и определить размерность линейного пространства решений системы
1. Записываем матрицу системы:
и с помощью элементарных преобразований преобразуем матрицу к треугольному виду, т.е. к такому виду, когда все элементы, находящиеся ниже главной диагонали равны нулю. Ранг матрицы системы равен числу линейно независимых строк, т.е., в нашем случае, числу строк, в которых остались ненулевые элементы:
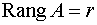
Размерность пространства решений равна 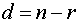
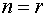
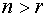
2. Выбираем 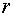
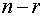
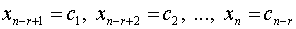
3. Записываем базис пространства решений системы полагая последовательно одну из свободных переменных равной единице, а остальные нулю. Размерность линейного пространства решений системы равна количеству векторов базиса.
Примечание. К элементарным преобразованиям матрицы относят:
1. умножение (деление) строки на множитель, отличный от нуля;
2. прибавление к какой-либо строке другой строки, умноженной на любое число;
3. перестановка строк местами;
4. преобразования 1–3 для столбцов (в случае решения систем линейных уравнений элементарные преобразования столбцов не используются).
Задача 3. Найти какой-нибудь базис и определить размерность линейного пространства решений системы.
Выписываем матрицу системы и с помощью элементарных преобразований приводим ее к треугольному виду:
Полагаем 

Размерность линейного пространства решений равна 3.
:: Рекомендуемая литература. Ремендуем покупать учебную литературу в интернет-магазине Озон
💡 Видео
Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

ФСР. Система однородных уравнений. Общее решениеСкачать

Высшая математика. Линейные пространства. Векторы. БазисСкачать

Базисные решения систем линейных уравнений (03)Скачать

Разложение вектора по векторам (базису). Аналитическая геометрия-1Скачать

4.1 Сумма и пересечение подпространств.Скачать

Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

ПАРАМЕТР ИЗ РЕАЛЬНОГО ЕГЭ | Ященко выдал БАЗУСкачать

Овчинников А. В. - Линейная алгебра - Понятие линейного пространства и его свойстваСкачать

Размерность суммы и пересечения подпространствСкачать

Найдите разложение вектора по векторам (базису)Скачать

Базис суммы и пересечения линейных пространствСкачать

3.2 Базис и размерность.Скачать

Базис и размерность. ТемаСкачать