Этот прием является особенно удобным в применении к линейным дифференциальным уравнениям. Проиллюстрируем его применение на примере уравнения второго порядка. Пусть дано дифференциальное уравнение второго порядка
Предположим, что коэффициенты и представляются в виде рядов, расположенных по целым положительным степеням , так что уравнение (1) можно переписать в виде
Решение этого уравнения будем искать также в виде степенного ряда
Подставляя это выражение и его производных в (2), получаем
Перемножая степенные ряды, собирая подобные члены и приравнивая нулю коэффициенты при всех степенях в левой части (4), получаем ряд уравнений:
Каждое последующее из уравнений (5) содержит одним искомым коэффициентом больше, чем предыдущее. Коэффициенты и остаются произвольными и играют роль произвольных постоянных. Первое из уравнений (5) дает , второе дает , третье — , и т.д. Вообще из (к + 1)-го уравнения можно определить , зная .
Практически удобно поступать следующим образом. Определим по описанной выше схеме два решения и , причем для выберем и , а для выберем и , что равносильно следующим начальными условиям:
Всякое решение уравнения (1) будет линейной комбинацией решений и .
Если начальные условия имеют вид , то очевидно,
Имеет место следующая теорема.
Теорема. Если ряды и сходятся при , то построенный указанным выше способом степенной ряд (3) будет также сходящимся при этих значениях и явится решением уравнения (1).
В частности, если и — многочлены от , то ряд (3) будет сходиться при любом значении .
Пример 1. Найти решения уравнения в виде степенного ряда.
Решение. Ищем в виде ряда , тогда
Подставляя и в (6), получаем
Приводя в (7) подобные члены и приравнивая нулю коэффициенты при всех степенях , получаем соотношения, из которых найдем коэффициенты
Положим для определенности, что . Тогда легко находим, что
Видео:Частное решение ДУ, с помощью рядаСкачать

Пример решения контрольной работы №2
Задание 1.
Для уравнения 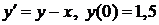
В данном случае





Подставим найденные значения производных в формулу (2):
Сравним найденное решение с решением в квадратурах. Запишем уравнение в виде: 


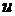
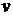
Решаем первое уравнение:

Подставим найденное решение во второе уравнение системы:
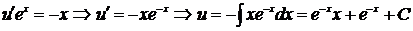
При нахождении неопределённого интеграла была использована формула интегрирования по частям. Тогда 

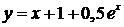
Для сравнения составим таблицу значений приближённого и точного решений на промежутке изменения х от — 1 до 1 с шагом 0,2.
| х | — 1 | — 0,8 | — 0,6 | — 0,4 | — 0,2 | |
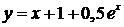 | 0,184 | 0,425 | 0,674 | 0,935 | 1,209 | 1,5 |
 | 0,1875 | 0,426 | 0,6747 | 0,948 | 1,213 | 1,5 |
| х | 0,2 | 0,4 | 0,6 | 0,8 | |
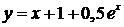 | 1,811 | 2,146 | 2,511 | 2,913 | 3,359 |
 | 1,8107 | 2,146 | 2,5107 | 2,9112 | 3,3542 |
Задание 2.Найти разложение в степенной ряд по степеням х решения дифференциального уравнения 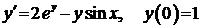
Решение ищем в виде ряда:

Согласно условию
тогда
Подставляя найденное значения производных в ряд, получим искомое решение дифференциального уравнения:
Задание 3
Разложить в ряд Фурье периодическую (с периодом 


Так как данная функция кусочно-монотонная и ограниченная, то она раскладывается в ряд Фурье.
Ряд Фурье для функции 

где коэффициенты 
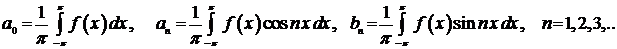
Находим коэффициенты ряда:

Следовательно,
Следовательно,
Ряд Фурье для данной функции имеет вид:
Контрольная работа № 2
Дисциплина «Дополнительные главы математики»
Направления 23.03.03.
Задание 1.
Решить дифференциальное уравнение 
а) приближённо, используя формулу Тейлора 
Сравнить полученные решения, составив таблицу значений на промежутке 
Задание 2.
Найти разложение в степенной ряд по степеням хрешения дифференциального уравнения 

Задание 3.
Разложить в ряд Фурье периодическую (с периодом 

Задание 1.
Решить дифференциальное уравнение 
а) приближённо, используя формулу Тейлора 
Сравнить полученные решения, составив таблицу значений на промежутке 
Задание 2.
Найти разложение в степенной ряд по степеням хрешения дифференциального уравнения 

Задание 3.
Разложить в ряд Фурье периодическую (с периодом 

Задание 1.
Решить дифференциальное уравнение 
а) приближённо, используя формулу Тейлора 
найдя, пять первых, отличных от нуля слагаемых;
Сравнить полученные решения, составив таблицу значений на промежутке 
Задание 2.
Найти разложение в степенной ряд по степеням х решения дифференциального уравнения 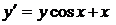

Задание 3.
Разложить в ряд Фурье периодическую (с периодом 
заданную на отрезке 
Задание 1.
Решить дифференциальное уравнение 
а) приближённо, используя формулу Тейлора 
Сравнить полученные решения, составив таблицу значений на промежутке 
Задание 2.
Найти разложение в степенной ряд по степеням хрешения дифференциального уравнения 

Задание 3.
Разложить в ряд Фурье периодическую (с периодом 

Задание 1.
Решить дифференциальное уравнение 
а) приближённо, используя формулу Тейлора 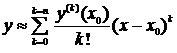
найдя, пять первых, отличных от нуля слагаемых;
Сравнить полученные решения, составив таблицу значений на промежутке 
Задание 2.
Найти разложение в степенной ряд по степеням хрешения дифференциального уравнения 

Задание 3.
Разложить в ряд Фурье периодическую (с периодом 

Задание 1.
Решить дифференциальное уравнение 
а) приближённо, используя формулу Тейлора 
Сравнить полученные решения, составив таблицу значений на промежутке 
Задание 2.
Найти разложение в степенной ряд по степеням хрешения дифференциального уравнения 

Задание 3.
Разложить в ряд Фурье периодическую (с периодом 

Задание 1.
Решить дифференциальное уравнение 
а) приближённо, используя формулу Тейлора 
Сравнить полученные решения, составив таблицу значений на промежутке 
Задание 2.
Найти разложение в степенной ряд по степеням хрешения дифференциального уравнения 

Задание 3.
Разложить в ряд Фурье периодическую (с периодом 

Задание 1.
Решить дифференциальное уравнение 
а) приближённо, используя формулу Тейлора 
Сравнить полученные решения, составив таблицу значений на промежутке, изменяя значения х с шагом 0,2.
Задание 2.
Найти разложение в степенной ряд по степеням хрешения дифференциального уравнения 

Задание 3.
Разложить в ряд Фурье периодическую (с периодом 
данную на отрезке 
Задание 1.
Решить дифференциальное уравнение 
а) приближённо, используя формулу Тейлора 
Сравнить полученные решения, составив таблицу значений на промежутке 
Задание 2.
Найти разложение в степенной ряд по степеням хрешения дифференциального уравнения 

Задание 3.
Разложить в ряд Фурье периодическую (с периодом 
данную на отрезке 
Задание 1.
Решить дифференциальное уравнение 
а) приближённо, используя формулу Тейлора 
Сравнить полученные решения, составив таблицу значений на промежутке, изменяя значения х с шагом 0,2.
Задание 2.
Найти разложение в степенной ряд по степеням х решения дифференциального уравнения 

Задание 3.
Разложить в ряд Фурье периодическую (с периодом 
данную на отрезке.
Оглавление
1.Обыкновенные дифференциальные уравнения и системы дифференциальных уравне — ний. 3
1.1. Основные определения и понятия………………………………………………………..3
1.2. Решение дифференциальных уравнений первого порядка с разделяющимися переме —
1.3. Решение однородных дифференциальных уравнений первого порядка……………….5
1.4. Решение линейных дифференциальных уравнений первого порядка и уравнений Бе —
1.5. Задачи на составление дифференциальных уравнений………………………………. 10
1.5.1. Задачи с геометрическим. содержанием на составление дифференциальных. уравне-
1.5.2. Задачи различного характера на составление дифференциальных уравнений……..14
1.6. Дифференциальные уравнения вида 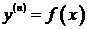
1.7. Линейные дифференциальные уравнения второго порядка с постоянными коэффици —
ентами и специальной правой частью………………………………..…………….…..19
1.8. Решение систем дифференциальных уравнений методом исключения неизвестных..21
1.9. Пример решения контрольной работы №1…………………………………. ………….23
2. Применение рядов к решению дифференциальных уравнений. Ряд Фурье…….….……33
2.1. Нахождение приближённого решения дифференциальных уравнений………. ……..33
2.2. Тригонометрические ряд. Ряд Фурье…………………………………………….……..33
2.3 Пример решения контрольной работы №2………………………………………………..35
Видео:Применение степенных рядов к решению дифференциальных уравнений.Скачать

Разложение функции в ряд Тейлора
Онлайн калькулятор для разложения функции в ряд Тейлора.
Ряд Те́йлора — разложение функции в бесконечную сумму степенных функций.
Ряд Тейлора был известен задолго до публикаций Тейлора — его использовали ещё в XVII веке Грегори, а также Ньютон.
Ряды Тейлора применяются при аппроксимации функции многочленами. В частности, линеаризация уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.
Данный калькулятор предназначен для разложения функции в ряд Тейлора онлайн.
Разложение Тейлора задается единственной формулой для функций, которые раскладывается в степенной ряд по степеням (x-a) в определенном интервале. Разложение ряда Тейлора по степеням x (при a=0) является частным случаем и называется разложением Маклорена.
Калькулятор поможет разложить функцию в ряд Тейлора онлайн. Для того чтобы получить решение, необходимо ввести соответствующие значения в ячейки: вид функции, значение x и степень, до которой нужно разложить ряд.
| Основные функции |
: x^a
📸 Видео
Примеры разложения в степенной рядСкачать

Дифференциальное уравнение ведет к разложению в ряд Тейлора и сумме ряда?Скачать

11.1 Разложение элементарных функций в ряд Маклорена (часть1)Скачать

Математический анализ, 39 урок, Формулы и ряды Тейлора и МаклоренаСкачать

Разложить функцию У по степеням (Х - 1)Скачать

Решение дифференциальных уравнений с помощью степенных рядов -3Скачать

12.3. Примеры разложения функций в ряд Тейлора. Часть 3.Скачать

301 Нахождение решения дифференци ального уравнения в виде степенного рядаСкачать

Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

#161. САМАЯ КРАСИВАЯ ФОРМУЛА В МАТЕМАТИКЕ — ФОРМУЛА ЭЙЛЕРА: e^(iπ)+1=0Скачать

Высшая математика СибГУТИ билет 6 продолжениеСкачать

Откуда взялся Ряд Тейлора? Простое объяснениеСкачать

Решение дифференциальных уравнений с помощью степенных рядов -2Скачать

Формула Тейлора за 3 минуты - bezbotvyСкачать

Разложения e^x и sin(x) в ряды Тейлора.Скачать

разложение функций в степенные рядыСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать










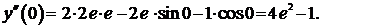
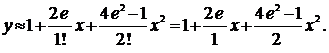
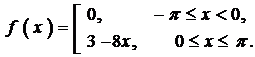








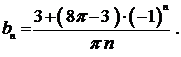






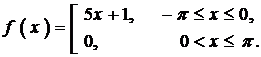





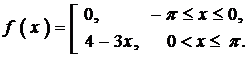

 : x^a
: x^a