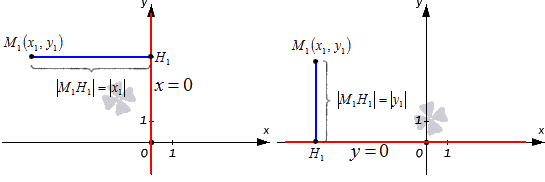- Формула для вычисления расстояния от точки до прямой в пространстве
- Вывод формулы вычисления расстояния от точки до прямой в пространстве
- Примеры задач на вычисление расстояния от точки до прямой в пространстве
- Математический портал
- Nav view search
- Navigation
- Search
- Прямая в пространстве, всевозможные уравнения.
- Расстояние от точки до прямой на плоскости и в пространстве: определение и примеры нахождения
- Расстояние от точки до прямой – определение
- Расстояние от точки до прямой на плоскости – теория, примеры, решения
- Решение задач на нахождение расстояния от заданной точки до заданной прямой на плоскости
- Расстояние от точки до прямой в пространстве – теория, примеры, решения
- Решение задач на нахождение расстояния от заданной точки до заданной прямой в пространстве
- 📸 Видео
Видео:18. Расстояние от точки до прямой в пространствеСкачать

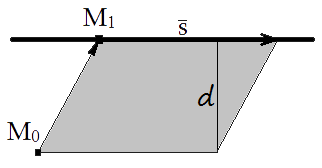
Формула для вычисления расстояния от точки до прямой в пространстве
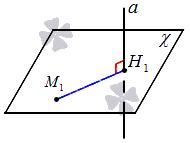
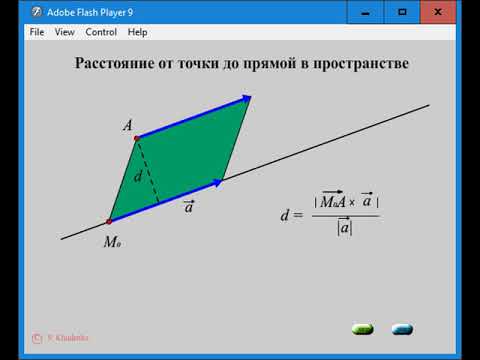
Если s = — направляющий вектор прямой l , M1( x 1, y 1, z 1) — точка лежащей на прямой, тогда расстояние от точки M0( x 0, y 0, z 0) до прямой l можно найти, используя формулу
| d = | | M0M1 × s | |
| | s | |
Видео:Расстояние от точки до прямойСкачать

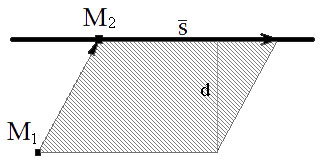
Вывод формулы вычисления расстояния от точки до прямой в пространстве
Если задано уравнение прямой l то несложно найти s = — направляющий вектор прямой и M1( x 1, y 1, z 1) — координаты точки лежащей на этой прямой. Из свойств векторного произведения известно, что модуль векторного произведения векторов равен площади параллелограмма построенного на этих векторах
С другой стороны площадь параллелограмма равна произведению его стороны на высоту проведенную к этой стороне
В нашем случае высота будет равна расстоянию от точки до плоскости d , а сторона параллелограмма равна модулю направляющего вектора s .
Приравняв площади несложно получить формулу расстояния от точки до прямой.
Видео:Лекция 24. Расстояние от точки до прямой на плоскости.Скачать

Примеры задач на вычисление расстояния от точки до прямой в пространстве
| x — 3 | = | y — 1 | = | z + 1 |
| 2 | 1 | 2 |
Из уравнения прямой получим:
s = — направляющий вектор прямой;
M1(3; 1; -1) — точка лежащая на прямой.
| M0M1 × s = | i | j | k | = |
| 3 | -1 | -4 | ||
| 2 | 1 | 2 |
d = | M0M1 × s | | s | = √ 2 2 + (-14) 2 + 5 2 √ 2 2 + 1 2 + 2 2 = √ 225 √ 9 = 15 3 = 5
Ответ: расстояние от точки до прямой равно 5.
Видео:7. Расстояние от точки до плоскости (вывод формулы примеры)Скачать

Математический портал
Видео:§15 Расстояние от точки до прямойСкачать

Nav view search
Navigation
Search
- Вы здесь:
- Home
- Аналитическая геометрия
- Высшая математика.
- Аналитическая геометрия.
- Прямая в пространстве, всевозможные уравнения, взаимное расположение прямых в пространстве, расстояние от точки до прямой в пространстве.
Видео:Определить расстояние от точки С до прямой АВ. Метод прямоугольного треугольника.Скачать

Прямая в пространстве, всевозможные уравнения.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
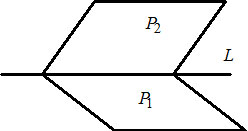
Существуют такие формы записи уравнения прямой в пространстве:
1) $left<beginA_1x+B_1y+C_1z+D_1=0quad (P_1)\ A_2x+B_2y+C_2z+D_2=0quad (P_2)endright. — $ общее уравнение прямой $L$ в пространстве, как линии пересечения двух плоскостей $P_1$ и $P_2.$
2) $frac=frac=frac
-$ каноническое уравнение прямой $L,$ которая проходит через точку $M(x_0, y_0, z_0)$ параллельно вектору $overline=(m, n, p).$ Вектор $overline S$ является направляющим вектором прямой $L.$
3) $frac=frac=frac -$ уравнение прямой, которая проходит через две точки $A(x_1, y_1, z_1)$ и $B(x_2, y_2, z_2).$
4) Приравнивая каждую из частей канонического уравнения 2 к прараметру $t,$ получаем параметрическое уравнение прямой:
Расположение двух прямых в пространстве.
Условие параллельности двух прямых: Прямые $L_1$ и $L_2$ параллельны тогда и только тогда, когда $overline_1paralleloverline_2Leftrightarrow$ $frac=frac=frac
.$
Условие перпендикулярности двух прямых: $L_1perp L_2Leftrightarrow$ $overline_1perpoverline_2Leftrightarrow$ $cdot+cdot+p_1cdot p_2=0.$
Угол между прямыми:
Расстояние от точки до прямой равно длине перпендикуляра, опущенного из точки на данную прямую.
Пусть прямая $L$ задана уравнением $frac=frac=frac
,$ следовательно $overline S=(m, n, p).$ Пусть также $M_2=(x_2, y_2, z_2) -$ произвольная точка, принадлежащая прямой $L.$ Тогда расстояние от точки $M_1=(x_1, y_1, z_1)$ до прямой $L$ можно найти по формуле: $$d(M_1, L)=frac<|[overline, overline S]|>.$$
Примеры.
2.198. Написать каноническое уравнение прямой, проходящей через точку $M_0(2, 0, -3)$ параллельно:
а) вектору $q(2, -3, 5);$
е) прямой $x=-2+t, y=2t, z=1-fract.$
Решение.
а) Воспользуемся формулой (2) уравнения прямой в пространстве:
$frac=frac=frac
-$ каноническое уравнение прямой $L,$ которая проходит через точку $M(x_0, y_0, z_0)$ параллельно вектору $overline=(m, n, p).$
По условию $M_0(2, 0, -3)$ и $overline=q(2,-3,5).$
б) Прямая, параллельная заданной прямой, должна быть параллельна ее направляющему вектору. Направляющий вектор прямой $frac=frac=frac$ имеет координаты $overline S(5, 2, -1).$ Далее, находим уравнение прямой проходящей точку $M_0(2, 0, -3)$ параллельно вектору $overline S(5, 2, -1)$ как и в пункте а):
в) ось OX имеет направляющий вектор $i=(1, 0, 0).$ Таким образом, ищем уравнение прямой проходящей точку $M_0(2, 0, -3)$ параллельно вектору $i(1, 0, 0):$
д) Прямая, заданная как пересечение двух плоскостей перпендикулярна нормалям обеих плоскостей , поэтому Направляющий вектор прямой
$left<begin3x-y+2z-7=0,\ x+3y-2z-3=0; endright.$ можно найти как векторное произведение нормалей заданных плоскостей.
Для плоскости $P_1:$ $3x-y+2z-7=0$ нормальный вектор имеет координаты $N_1(3, -1, 2);$
для плосости $P_2:$ $x+3y-2z-3,$ нормальный вектор имеет координаты $N_2(1, 3, -2).$
Находим векторное произведение:
Таким образом, направляющий вектор прямой $left<begin3x-y+2z-7=0,\ x+3y-2z-3=0; endright.$ имеет координаты $overline S (-4, 8, 10).$
Далее нам необходимо найти уравнение прямой проходящей точку $M_0(2, 0, -3)$ параллельно вектору $overline S(-4, 8, 10):$
е) Найдем направляющий вектор прямой $x=-2+t, y=2t, z=1-fract.$ Для этого запишем уравнение этой прямой в каноническом виде:
Отсюда находим направляющий вектор $overline Sleft(1, 2, -fracright).$ Умножим координаты направляющего вектора на 2 (чтобы избавиться от дроби): $overline S_1(2, 4, -1).$
Далее нам необходимо найти уравнение прямой проходящей точку $M_0(2, 0, -3)$ параллельно вектору $overline S(2, 4, -1):$
2.199(a). Написать уравнение прямой, проходящей через две заданные точки $M_1 (1, -2, 1)$ и $M_2(3, 1, -1).$
Решение.
Воспользуемся формулой (3) уравнения прямой в пространстве:
$frac=frac=frac -$ уравнение прямой, которая проходит через две точки $A(x_1, y_1, z_1)$ и $B(x_2, y_2, z_2).$
Подставляем заданные точки:
2.204. Найти расстояние между параллельными прямыми
Решение.
Расстояние между параллельными прямыми $L_1$ и $L_2$ равно расстоянию от произвольной точки прямой $L_1$ до прямой $L_2.$ Следовательно, его можно найти по формуле $$d(L_1, L_2)=d(M_1, L_2)=frac<|[overline, overline S]|>,$$ где $M_1-$ произвольная точка прямой $L_1,$ $M_2 — $произвольная точка прямой $L_2,$ $overline S -$ направляющий вектор прямой $L_2.$
Из канонических уравнений прямых берем точки $M_1=(2, -1, 0)in L_1,$ $M_2=(7, 1, 3)in L_2,$ $overline S=(3, 4, 2). $
Отсюда находим $overline=(7-2, 1-(-1),3-0)=(5, 2, 3);$
Ответ: 3.
2.205 (а). Найти расстояние от точки $A(2, 3, -1)$ до заданной прямой $L:$ $left<begin2x-2y+z+3=0,\ 3x-2y+2z+17=0 endright.$
Решение.
Для того, чтобы найти расстояние от точки $A$ до прямой $L,$ нам необходимо выбрать произвольную точку $M,$ принадлежащую прямой $L$ и найти направляющий вектор этой прямой.
Выбираем точку $M.$ Пусть координата $z=0.$ Подставим это значение в данную систему:
Таким образом, $M=(-14, -frac, 0)$
Направляющий вектор найдем, как векторное произведение нормалей заданных плоскостей:
Для плоскости $P_1:$ $2x-2y+z+3=0$ нормальный вектор имеет координаты $N_1(2, -2, 1);$
для плосости $P_2:$ $3x+2y+2z+17=0,$ нормальный вектор имеет координаты $N_2(3, -2, 2).$
Находим векторное произведение:
Таким образом, направляющий вектор прямой $left<begin2x-2y+z+3=0,\ 3x-2y+2z+17=0 endright.$
имеет координаты $overline S (-2, -1, 2).$
Теперь можно воспользоваться формулой $$d(A, L)=frac<|[overline, overline S]|>.$$
$overline=left(2-(-14),3-left(-fracright),-1-0right)=left(16, 15frac, -1right)$
Ответ: $d(A, L)=15.$
2.212. Написать каноническое уравнение прямой, которая проходит через точку $M_0(3, -2, -4)$ параллельно плоскости $P: 3x-2y-3z-7=0$ и пересекает прямую $L: frac=frac=frac.$
Решение.
Запишем уравнение плоскости $P_1,$ которая проходит через точку $M_0(3, -2, -4)$ параллельно плоскости $3x-2y-3z-7=0:$
$P: 3x-2y-3z-7=0Rightarrow overline N=(3; -2; -3).$ Искомая плоскость проходит через точку $M_0(3, -2, -4)$ перпендикулярно вектору $overline N(3, -2, -3).$
$P_1: 3x-9-2y-4-3z-12=0 Rightarrow$
Далее найдем точку пересечения плоскости $P_1$ и прямой $L.$ Для этого запишем уравнение прямой $L$ в параметрической форме:
Далее, подставим значения $x, y$ и $z,$ выраженные через $t$ в уравнение плоскости $P_1,$ и из полученного уравнения выразм $t:$
Подставляя найденное занчение $t$ в уравнение прямой $L,$ найдем координаты точки пересечения:
Таким образом, прямая $L$ и плоскость $P_1$ пересекаются в точке $M_1(8, -8, 5).$
Теперь запишем уравнение прямой, проходящей через точки $M_0(3, -2. -4)$ и $M_1(8, -8, 5)$— это и будет искомая прямая. Воспользуемся формулой ( 3) $frac=frac=frac :$
2.199.
б) Написать уравнение прямой, проходящей через две заданные точки $M_1 (3, -1, 0)$ и $M_2(1, 0, -3).$
б) Найти расстояние от точки $A(2, 3, -1)$ до заданной прямой $ L:$ $left<beginx=3t+5,\ y=2t,\z=-2t-25. endright.$
2.206. Доказать, что прямые $L_1: left<begin2x+2y-z-10=0,\ x-y-z-22=0, endright.$ и $L_2: frac=frac=frac.$ параллельны и найти расстояние $rho(L_1, L_2)$
2.207. Составить уравнения прямой, проходящей через точки пересечения плоскости $x-3y+2z+1=0$ с прямыми $frac=frac=frac$ и $frac=frac=frac.$
2.211. Написать уравнение прямой, проходящей через точку $M_0(7, 1, 0)$ параллельно плоскости $2x+3y-z-15=0$ и пересекающей прямую $frac=frac=frac.$
Видео:7 класс, 38 урок, Расстояние от точки до прямой. Расстояние между параллельными прямымиСкачать

Расстояние от точки до прямой на плоскости и в пространстве: определение и примеры нахождения
Данная статья рассказывает о теме «расстояния от точки до прямой», рассматриваются определения расстояния от точки к прямой с иллюстрированными примерами методом координат. Каждый блок теории в конце имеет показанные примеры решения подобных задач.
Видео:Расстояние от точки до плоскости / Вывод формулыСкачать

Расстояние от точки до прямой – определение
Расстояние от точки до прямой находится через определение расстояния от точки до точки. Рассмотрим подробней.
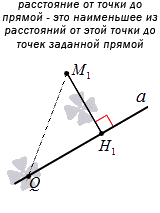
Пусть имеется прямая a и точка М 1 , не принадлежащая заданной прямой. Через нее проведем прямую b , расположенную перпендикулярно относительно прямой a . Точка пересечения прямых возьмем за Н 1 . Получим, что М 1 Н 1 является перпендикуляром, который опустили из точки М 1 к прямой a .
Расстоянием от точки М 1 к прямой a называется расстояние между точками М 1 и Н 1 .
Бывают записи определения с фигурированием длины перпендикуляра.
Расстоянием от точки до прямой называют длину перпендикуляра, проведенного из данной точки к данной прямой.
Определения эквивалентны. Рассмотрим рисунок, приведенный ниже.
Известно, что расстояние от точки до прямой является наименьшим из всех возможных. Рассмотрим это на примере.
Если взять точку Q , лежащую на прямой a , не совпадающую с точкой М 1 , тогда получим, что отрезок М 1 Q называется наклонной, опущенной из М 1 к прямой a . Необходимо обозначить, что перпендикуляр из точки М 1 является меньше, чем любая другая наклонная, проведенная из точки к прямой.
Чтобы доказать это, рассмотрим треугольник М 1 Q 1 Н 1 , где М 1 Q 1 является гипотенузой. Известно, что ее длина всегда больше длины любого из катетов. Значим, имеем, что M 1 H 1 M 1 Q . Рассмотрим рисунок, приведенный ниже.
Видео:Расстояние от точки до прямой | Вывод формулы через Подобие и ПифагораСкачать

Расстояние от точки до прямой на плоскости – теория, примеры, решения
Исходные данные для нахождения от точки до прямой позволяют использовать несколько методов решения: через теорему Пифагора, определения синуса, косинуса, тангенса угла и другими. Большинство заданий такого типа решают в школе на уроках геометрии.
Когда при нахождении расстояния от точки до прямой можно ввести прямоугольную систему координат, то применяют метод координат. В данном пункте рассмотрим основных два метода нахождения искомого расстояния от заданной точки.
Первый способ подразумевает поиск расстояния как перпендикуляра, проведенного из М 1 к прямой a . Во втором способе используется нормальное уравнение прямой а для нахождения искомого расстояния.
Если на плоскости имеется точка с координатами M 1 ( x 1 , y 1 ) , расположенная в прямоугольной системе координат, прямая a , а необходимо найти расстояние M 1 H 1 , можно произвести вычисление двумя способами. Рассмотрим их.
Если имеются координаты точки H 1 , равные x 2 , y 2 , тогда расстояние от точки до прямой вычисляется по координатам из формулы M 1 H 1 = ( x 2 — x 1 ) 2 + ( y 2 — y 1 ) 2 .
Теперь перейдем к нахождению координат точки Н 1 .
Известно, что прямая линия в О х у соответствует уравнению прямой на плоскости. Возьмем способ задания прямой a через написание общего уравнения прямой или уравнения с угловым коэффициентом. Составляем уравнение прямой, которая проходит через точку М 1 перпендикулярно заданной прямой a . Прямую обозначим буковой b . Н 1 является точкой пересечения прямых a и b , значит для определения координат необходимо воспользоваться статьей, в которой идет речь о координатах точек пересечения двух прямых.
Видно, что алгоритм нахождения расстояния от заданной точки M 1 ( x 1 , y 1 ) до прямой a проводится согласно пунктам:
- нахождение общего уравнения прямой a , имеющее вид A 1 x + B 1 y + C 1 = 0 ,или уравнение с угловым коэффициентом, имеющее вид y = k 1 x + b 1 ;
- получение общего уравнения прямой b , имеющее вид A 2 x + B 2 y + C 2 = 0 или уравнение с угловым коэффициентом y = k 2 x + b 2 , если прямая b пересекает точку М 1 и является перпендикулярной к заданной прямой a ;
- определение координат x 2 , y 2 точки Н 1 , являющейся точкой пересечения a и b , для этого производится решение системы линейных уравнений A 1 x + B 1 y + C 1 = 0 A 2 x + B 2 y + C 2 = 0 или y = k 1 x + b 1 y = k 2 x + b 2 ;
- вычисление искомого расстояния от точки до прямой, используя формулу M 1 H 1 = ( x 2 — x 1 ) 2 + ( y 2 — y 1 ) 2 .
Теорема способна помочь ответить на вопрос о нахождении расстояния от заданной точки до заданной прямой на плоскости.
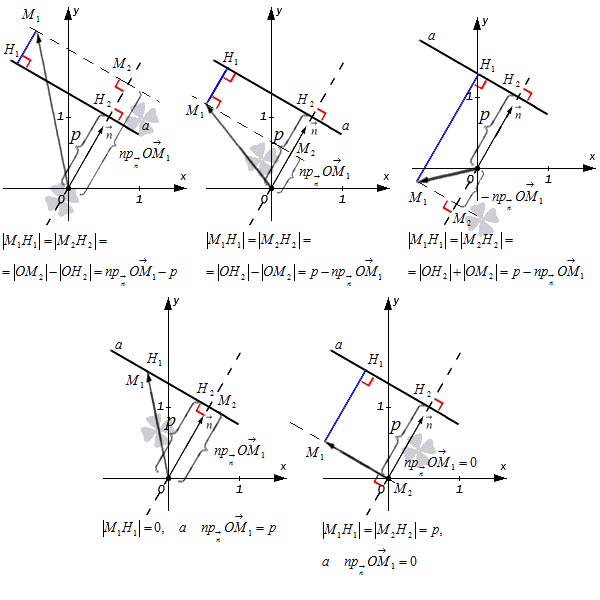
Прямоугольная система координат имеет О х у имеет точку M 1 ( x 1 , y 1 ) , из которой проведена прямая а к плоскости, задаваемая нормальным уравнением плоскости, имеющее вид cos α · x + cos β · y — p = 0 , равно по модулю значению, получаемому в левой части нормального уравнения прямой, вычисляемому при x = x 1 , y = y 1 , значит, что M 1 H 1 = cos α · x 1 + cos β · y 1 — p .
Прямой а соответствует нормальное уравнение плоскости, имеющее вид cos α · x + cos β · y — p = 0 , тогда n → = ( cos α , cos β ) считается нормальным вектором прямой a при расстоянии от начала координат до прямой a с p единицами. Необходимо изобразить все данные на рисунке, добавить точку с координатами M 1 ( x 1 , y 1 ) , где радиус-вектор точки М 1 — O M 1 → = ( x 1 , y 1 ) . Необходимо провести прямую от точки до прямой, которое обозначим M 1 H 1 . Необходимо показать проекции М 2 и Н 2 точек М 1 и Н 2 на прямую, проходящую через точку O с направляющим вектором вида n → = ( cos α , cos β ) , а числовую проекцию вектора обозначим как O M 1 → = ( x 1 , y 1 ) к направлению n → = ( cos α , cos β ) как n p n → O M 1 → .
Вариации зависят от расположения самой точки М 1 . Рассмотрим на рисунке, приведенном ниже.
Результаты фиксируем при помощи формулы M 1 H 1 = n p n → O M → 1 — p . После чего приводим равенство к такому виду M 1 H 1 = cos α · x 1 + cos β · y 1 — p для того, чтобы получить n p n → O M → 1 = cos α · x 1 + cos β · y 1 .
Скалярное произведение векторов в результате дает преобразованную формулу вида n → , O M → 1 = n → · n p n → O M 1 → = 1 · n p n → O M 1 → = n p n → O M 1 → , которая является произведением в координатной форме вида n → , O M 1 → = cos α · x 1 + cos β · y 1 . Значит, получаем, что n p n → O M 1 → = cos α · x 1 + cos β · y 1 . Отсюда следует, что M 1 H 1 = n p n → O M 1 → — p = cos α · x 1 + cos β · y 1 — p . Теорема доказана.
Получаем, что для нахождения расстояния от точки M 1 ( x 1 , y 1 ) к прямой a на плоскости необходимо выполнить несколько действий:
- получение нормального уравнения прямой a cos α · x + cos β · y — p = 0 , при условии, что его нет в задании;
- вычисление выражения cos α · x 1 + cos β · y 1 — p , где полученное значение принимает M 1 H 1 .
Видео:Расстояние от точки до прямой в пространствеСкачать
Решение задач на нахождение расстояния от заданной точки до заданной прямой на плоскости
Применим данные методы на решении задач с нахождением расстояния от точки до плоскости.
Найти расстояние от точки с координатами M 1 ( — 1 , 2 ) к прямой 4 x — 3 y + 35 = 0 .
Применим первый способ для решения.
Для этого необходимо найти общее уравнение прямой b , которая проходит через заданную точку M 1 ( — 1 , 2 ) , перпендикулярно прямой 4 x — 3 y + 35 = 0 . Из условия видно, что прямая b является перпендикулярной прямой a , тогда ее направляющий вектор имеет координаты, равные ( 4 , — 3 ) . Таким образом имеем возможность записать каноническое уравнение прямой b на плоскости, так как имеются координаты точки М 1 , принадлежит прямой b . Определим координаты направляющего вектора прямой b . Получим, что x — ( — 1 ) 4 = y — 2 — 3 ⇔ x + 1 4 = y — 2 — 3 . Полученное каноническое уравнение необходимо преобразовать к общему. Тогда получаем, что
x + 1 4 = y — 2 — 3 ⇔ — 3 · ( x + 1 ) = 4 · ( y — 2 ) ⇔ 3 x + 4 y — 5 = 0
Произведем нахождение координат точек пересечения прямых, которое примем за обозначение Н 1 . Преобразования выглядят таким образом:
4 x — 3 y + 35 = 0 3 x + 4 y — 5 = 0 ⇔ x = 3 4 y — 35 4 3 x + 4 y — 5 = 0 ⇔ x = 3 4 y — 35 4 3 · 3 4 y — 35 4 + 4 y — 5 = 0 ⇔ ⇔ x = 3 4 y — 35 4 y = 5 ⇔ x = 3 4 · 5 — 35 4 y = 5 ⇔ x = — 5 y = 5
Из выше написанного имеем, что координаты точки Н 1 равны ( — 5 ; 5 ) .
Необходимо вычислить расстояние от точки М 1 к прямой a . Имеем, что координаты точек M 1 ( — 1 , 2 ) и H 1 ( — 5 , 5 ) , тогда подставляем в формулу для нахождения расстояния и получаем, что
M 1 H 1 = ( — 5 — ( — 1 ) 2 + ( 5 — 2 ) 2 = 25 = 5
Второй способ решения.
Для того, чтобы решить другим способом, необходимо получить нормальное уравнение прямой. Вычисляем значение нормирующего множителя и умножаем обе части уравнения 4 x — 3 y + 35 = 0 . Отсюда получим, что нормирующий множитель равен — 1 4 2 + ( — 3 ) 2 = — 1 5 , а нормальное уравнение будет вида — 1 5 · 4 x — 3 y + 35 = — 1 5 · 0 ⇔ — 4 5 x + 3 5 y — 7 = 0 .
По алгоритму вычисления необходимо получить нормальное уравнение прямой и вычислить его со значениями x = — 1 , y = 2 . Тогда получаем, что
— 4 5 · — 1 + 3 5 · 2 — 7 = — 5
Отсюда получаем, что расстояние от точки M 1 ( — 1 , 2 ) к заданной прямой 4 x — 3 y + 35 = 0 имеет значение — 5 = 5 .
Видно, что в данном методе важно использование нормального уравнения прямой, так как такой способ является наиболее коротким. Но первый метод удобен тем, что последователен и логичен, хотя имеет больше пунктов вычисления.
На плоскости имеется прямоугольная система координат О х у с точкой M 1 ( 8 , 0 ) и прямой y = 1 2 x + 1 . Найти расстояние от заданной точки до прямой.
Решение первым способом подразумевает приведение заданного уравнения с угловым коэффициентом к уравнению общего вида. Для упрощения можно сделать иначе.
Если произведение угловых коэффициентов перпендикулярных прямых имеют значение — 1 , значит угловой коэффициент прямой перпендикулярной заданной y = 1 2 x + 1 имеет значение 2 . Теперь получим уравнение прямой, проходящее через точку с координатами M 1 ( 8 , 0 ) . Имеем, что y — 0 = — 2 · ( x — 8 ) ⇔ y = — 2 x + 16 .
Переходим к нахождению координат точки Н 1 , то есть точкам пересечения y = — 2 x + 16 и y = 1 2 x + 1 . Составляем систему уравнений и получаем:
y = 1 2 x + 1 y = — 2 x + 16 ⇔ y = 1 2 x + 1 1 2 x + 1 = — 2 x + 16 ⇔ y = 1 2 x + 1 x = 6 ⇔ ⇔ y = 1 2 · 6 + 1 x = 6 = y = 4 x = 6 ⇒ H 1 ( 6 , 4 )
Отсюда следует, что расстояние от точки с координатами M 1 ( 8 , 0 ) к прямой y = 1 2 x + 1 равно расстоянию от точки начала и точки конца с координатами M 1 ( 8 , 0 ) и H 1 ( 6 , 4 ) . Вычислим и получим, что M 1 H 1 = 6 — 8 2 + ( 4 — 0 ) 2 20 = 2 5 .
Решение вторым способом заключается в переходе от уравнения с коэффициентом к нормальному его виду. То есть получим y = 1 2 x + 1 ⇔ 1 2 x — y + 1 = 0 , тогда значение нормирующего множителя будет — 1 1 2 2 + ( — 1 ) 2 = — 2 5 . Отсюда следует, что нормальное уравнение прямой принимает вид — 2 5 · 1 2 x — y + 1 = — 2 5 · 0 ⇔ — 1 5 x + 2 5 y — 2 5 = 0 . Произведем вычисление от точки M 1 8 , 0 к прямой вида — 1 5 x + 2 5 y — 2 5 = 0 . Получаем:
M 1 H 1 = — 1 5 · 8 + 2 5 · 0 — 2 5 = — 10 5 = 2 5
Необходимо вычислить расстояние от точки с координатами M 1 ( — 2 , 4 ) к прямым 2 x — 3 = 0 и y + 1 = 0 .
Получаем уравнение нормального вида прямой 2 x — 3 = 0 :
2 x — 3 = 0 ⇔ 1 2 · 2 x — 3 = 1 2 · 0 ⇔ x — 3 2 = 0
После чего переходим к вычислению расстояния от точки M 1 — 2 , 4 к прямой x — 3 2 = 0 . Получаем:
M 1 H 1 = — 2 — 3 2 = 3 1 2
Уравнение прямой y + 1 = 0 имеет нормирующий множитель со значением равным -1. Это означает, что уравнение примет вид — y — 1 = 0 . Переходим к вычислению расстояния от точки M 1 ( — 2 , 4 ) к прямой — y — 1 = 0 . Получим, что оно равняется — 4 — 1 = 5 .
Ответ: 3 1 2 и 5 .
Подробно рассмотрим нахождение расстояния от заданной точки плоскости к координатным осям О х и О у .
В прямоугольной системе координат у оси О у имеется уравнение прямой, которое является неполным имеет вида х = 0 , а О х — y = 0 . Уравнения являются нормальными для осей координат, тогда необходимо найти расстояние от точки с координатами M 1 x 1 , y 1 до прямых. Это производится, исходя из формул M 1 H 1 = x 1 и M 1 H 1 = y 1 . Рассмотрим на рисунке, приведенном ниже.
Найти расстояние от точки M 1 ( 6 , — 7 ) до координатных прямых, расположенных в плоскости О х у .
Так как уравнение у = 0 относится к прямой О х , можно найти расстояние от M 1 с заданными координатами, до этой прямой, используя формулу. Получаем, что 6 = 6 .
Так как уравнение х = 0 относится к прямой О у , то можно найти расстояние от М 1 к этой прямой по формуле. Тогда получим, что — 7 = 7 .
Ответ: расстояние от М 1 к О х имеет значение 6 , а от М 1 к О у имеет значение 7 .
Видео:9 класс, 7 урок, Уравнение прямойСкачать

Расстояние от точки до прямой в пространстве – теория, примеры, решения
Когда в трехмерном пространстве имеем точку с координатами M 1 ( x 1 , y 1 , z 1 ) , необходимо найти расстояние от точки A до прямой a .
Рассмотрим два способа, которые позволяют производить вычисление расстояние от точки до прямой a , расположенной в пространстве. Первый случай рассматривает расстояние от точки М 1 к прямой, где точка на прямой называется Н 1 и является основанием перпендикуляра, проведенного из точки М 1 на прямую a . Второй случай говорит о том, что точки этой плоскости необходимо искать в качестве высоты параллелограмма.
Из определения имеем, что расстояние от точки М 1 , расположенной на прямой а, является длиной перпендикуляра М 1 Н 1 , тогда получим, что при найденных координатах точки Н 1 , тогда найдем расстояние между M 1 ( x 1 , y 1 , z 1 ) и H 1 ( x 1 , y 1 , z 1 ) , исходя из формулы M 1 H 1 = x 2 — x 1 2 + y 2 — y 1 2 + z 2 — z 1 2 .
Получаем, что все решение идет к тому, чтобы найти координаты основания перпендикуляра, проведенного из М 1 на прямую a . Это производится следующим образом: Н 1 является точкой, где пересекаются прямая a с плоскостью, которая проходит через заданную точку.
Значит, алгоритм определения расстояния от точки M 1 ( x 1 , y 1 , z 1 ) к прямой a пространства подразумевает несколько пунктов:
- составление уравнение плоскости χ в качестве уравнения плоскости, проходящего через заданную точку, находящуюся перпендикулярно прямой;
- определение координат ( x 2 , y 2 , z 2 ) , принадлежавших точке Н 1 , которая является точкой пересечения прямой a и плоскости χ ;
- вычисление расстояния от точки до прямой при помощи формулы M 1 H 1 = x 2 — x 1 2 + y 2 — y 1 2 + z 2 — z 1 2 .
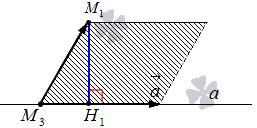
Из условия имеем прямую a , тогда можем определить направляющий вектор a → = a x , a y , a z с координатами x 3 , y 3 , z 3 и определенной точки М 3 ,принадлежащей прямой a . При наличии координат точек M 1 ( x 1 , y 1 ) и M 3 x 3 , y 3 , z 3 можно произвести вычисление M 3 M 1 → :
M 3 M 1 → = ( x 1 — x 3 , y 1 — y 3 , z 1 — z 3 )
Следует отложить векторы a → = a x , a y , a z и M 3 M 1 → = x 1 — x 3 , y 1 — y 3 , z 1 — z 3 из точки М 3 , соединим и получим фигуру параллелограмма. М 1 Н 1 является высотой параллелограмма.
Рассмотрим на рисунке, приведенном ниже.
Имеем, что высота М 1 Н 1 является искомым расстоянием, тогда необходимо найти его по формуле. То есть ищем M 1 H 1 .
Обозначим площадь параллелограмма за букву S , находится по формуле, используя вектор a → = ( a x , a y , a z ) и M 3 M 1 → = x 1 — x 3 . y 1 — y 3 , z 1 — z 3 . Формула площади имеет вид S = a → × M 3 M 1 → . Также площадь фигуры равняется произведению длин его сторон на высоту, получим, что S = a → · M 1 H 1 с a → = a x 2 + a y 2 + a z 2 , являющимся длиной вектора a → = ( a x , a y , a z ) , являющейся равной стороне параллелограмма. Значит, M 1 H 1 является расстоянием от точки до прямой. Ее нахождение производится по формуле M 1 H 1 = a → × M 3 M 1 → a → .
Для нахождения расстояния от точки с координатами M 1 ( x 1 , y 1 , z 1 ) до прямой a в пространстве, необходимо выполнить несколько пунктов алгоритма:
- определение направляющего вектора прямой a — a → = ( a x , a y , a z ) ;
- вычисление длины направляющего вектора a → = a x 2 + a y 2 + a z 2 ;
- получение координат x 3 , y 3 , z 3 , принадлежавших точке М3, находящейся на прямой а;
- вычисление координат вектора M 3 M 1 → ;
- нахождение векторного произведения векторов a → ( a x , a y , a z ) и M 3 M 1 → = x 1 — x 3 , y 1 — y 3 , z 1 — z 3 в качестве a → × M 3 M 1 → = i → j → k → a x a y a z x 1 — x 3 y 1 — y 3 z 1 — z 3 для получения длины по формуле a → × M 3 M 1 → ;
- вычисление расстояния от точки до прямой M 1 H 1 = a → × M 3 M 1 → a → .
Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Решение задач на нахождение расстояния от заданной точки до заданной прямой в пространстве
Найти расстояние от точки с координатами M 1 2 , — 4 , — 1 к прямой x + 1 2 = y — 1 = z + 5 5 .
Первый способ начинается с записи уравнения плоскости χ , проходящей через М 1 и перпендикулярно заданной точке. Получаем выражение вида:
2 · ( x — 2 ) — 1 · ( y — ( — 4 ) ) + 5 · ( z — ( — 1 ) ) = 0 ⇔ 2 x — y + 5 z — 3 = 0
Нужно найти координаты точки H 1 , являющейся точкой пересечения с плоскостью χ к заданной по условию прямой. Следует переходить от канонического вида к пересекающемуся. Тогда получаем систему уравнений вида:
x + 1 2 = y — 1 = z + 5 5 ⇔ — 1 · ( x + 1 ) = 2 · y 5 · ( x + 1 ) = 2 · ( z + 5 ) 5 · y = — 1 · ( z + 5 ) ⇔ x + 2 y + 1 = 0 5 x — 2 z — 5 = 0 5 y + z + 5 = 0 ⇔ x + 2 y + 1 = 0 5 x — 2 z — 5 = 0
Необходимо вычислить систему x + 2 y + 1 = 0 5 x — 2 z — 5 = 0 2 x — y + 5 z — 3 = 0 ⇔ x + 2 y = — 1 5 x — 2 z = 5 2 x — y + 5 z = 3 по методу Крамера, тогда получаем, что:
∆ = 1 2 0 5 0 — 2 2 — 1 5 = — 60 ∆ x = — 1 2 0 5 0 — 2 3 — 1 5 = — 60 ⇔ x = ∆ x ∆ = — 60 — 60 = 1 ∆ y = 1 — 1 0 5 5 2 2 3 5 = 60 ⇒ y = ∆ y ∆ = 60 — 60 = — 1 ∆ z = 1 2 — 1 5 0 5 2 — 1 3 = 0 ⇒ z = ∆ z ∆ = 0 — 60 = 0
Отсюда имеем, что H 1 ( 1 , — 1 , 0 ) .
Необходимо рассчитать расстояние между точками с координатами M 1 ( 2 , — 4 , — 1 ) и H 1 ( 1 , — 1 , 0 ) по формуле:
M 1 H 1 = 1 — 2 2 + — 1 — — 4 2 + 0 — — 1 2 = 11
Второй способ необходимо начать с поиска координат в каноническом уравнении. Для этого необходимо обратит внимание на знаменатели дроби. Тогда a → = 2 , — 1 , 5 является направляющим вектором прямой x + 1 2 = y — 1 = z + 5 5 . Необходимо вычислить длину по формуле a → = 2 2 + ( — 1 ) 2 + 5 2 = 30 .
Понятно, что прямая x + 1 2 = y — 1 = z + 5 5 пересекает точку M 3 ( — 1 , 0 , — 5 ) , отсюда имеем, что вектор с началом координат M 3 ( — 1 , 0 , — 5 ) и его концом в точке M 1 2 , — 4 , — 1 является M 3 M 1 → = 3 , — 4 , 4 . Находим векторное произведение a → = ( 2 , — 1 , 5 ) и M 3 M 1 → = ( 3 , — 4 , 4 ) .
Мы получаем выражение вида a → × M 3 M 1 → = i → j → k → 2 — 1 5 3 — 4 4 = — 4 · i → + 15 · j → — 8 · k → + 20 · i → — 8 · j → = 16 · i → + 7 · j → — 5 · k →
получаем, что длина векторного произведения равняется a → × M 3 M 1 → = 16 2 + 7 2 + — 5 2 = 330 .
Имеются все данные для использования формулы вычисления расстояния от точки для прямлой, поэтому применим ее и получим:
M 1 H 1 = a → × M 3 M 1 → a → = 330 30 = 11
📸 Видео
Расстояние от точки до прямой (метод координат)Скачать

Формула расстояния от точки до прямой (на плоскости)Скачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Вопрос-ответ с астрономом Владимиром Сурдиным – Самые популярные вопросыСкачать

Прямая на плоскости. Проекция точки на прямуюСкачать

Видеоурок "Расстояние от точки до прямой"Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Видеоурок "Расстояние от точки до прямой"Скачать