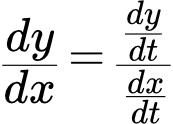Найти производную по параметру дифференциальные уравнения (6 видео)

Дифференцируемость решения по параметру и ее применения по начальным условиям

По этой ссылке вы найдёте полный курс лекций по математике:

Рассматривается система уравнений с параметром ц При каждом /i система имеет решение. Оно зависит не только от ty но и от выбранного значения параметра поэтому обозначается x(t, р). Теорема 1. Пусть при — область в Rn+I, М — интервал в R1) все функции a'(fi) непрерывны. Пусть при всех ft € М на отрезке t2] Э t0 решение x(t,p) задачи (1) существует и проходит в области D. Тогда это решение имеет производные dxjdp, непрерывные по (;t, ц).

Функции V4 = Qxjdp. (i = 1. п) удовлетворяют системе уравнений в вариациях В (2) производные от /• зависят от аргументов J, «j /i). xn(t9fi)9fi9 где — координаты решения /*) при том значении при котором разыскивается дх/др. Если решение x(t, ц) известно хотя бы при одном значении д, то система^!), позволяет найти дх/дц при этом ft. Систему (2) можно не запоминать, она получается посредством дифференцирования обеих частей системы (1) по l при этом считаем, что х = x(t, /х), и дх</дц обозначаем и.. I Пример 1.

Найти дх/дц при l — 0 от решения задачи Дифференцируемость решения по параметру и ее применения по начальным условиям. Решение примера. Условия теоремы 1 выполнены, так как функции / = х2 + 4fit р? и a(fi) = 2/i — 1 непрерывны и имеют непрерывные производные по х и ц. Дифференцируя (3) по ц и обозначая х^ = и, получаем Здесь i = 0, а х — решение задачи (3) при ц = О, то есть задачи dx/dt = ж2, ж(1) = -1. Отсюда а: = -1 ft.

Теперь (4) принимает вид Решая это линейное уравнение (выкладки пропускаем), получаем и = t2 + d

2. Из начального условия находим с = 1. Итак, Доказательство теоремы. Зафиксируем /х € М. Имеем где — решение задачи (1), но с Д вместо ji, то есть Обозначим дробь в (5) через Д). Идея доказательства теоремы. Составляем дифференциальное уравнение для v(t9 Д) при Д Ф fi.

Его правая часть при Д /х стремится к правой части уравнения (2).

Поэтому и решение v(t9 Д) при Д /х, то есть дробь в (5), стремится к решению уравнения (2). Значит, предел в (5), то есть дх/дц9 существует и удовлетворяет уравнению (2). Из уравнений (6) и (1), вычитая и деля на Д — р, получаем Преобразуем первую дробь в (7). Положим Тогда Поэтому из (7) имеем Так как df/dx, df/Зц непрерывны по совокупности переменных, то подынтегральные функции непрерывны по , а интегралы непрерывно по t. Из (6) по теореме 7 §7 ж непрерывно по (;t, Д) — по совокупности переменных.

Поэтому последние два интеграла в (8) — непрерывные функции от Д), включая значение Д = Обозначая их #(*,Д) и Л(*,Д), получаем Функция v(t9 Ji) была определена при Д Ф ц. Доопределяем ее при Д = /м как решение уравнения (9) с начальным условием и(*0, ц) = a'(/i), полученным из начального условия (7) при . По теореме 7 §7 функция v(t9JT) непрерывна по Д, включая Д = /х.

Возможно вам будут полезны данные страницы:

При Д = /х имеем х* = х = /*), /1* = ц9 подынтегральные выражения в (8) не зависят от 8. Тогда в (9) матрица Я и вектор h принимают значения Таким образом, для v(t9fi) уравнение (9) и начальное условие v(t0,n) = a'(fi) совпадают с (2), то есть v(t9fi) удовлетворяет (2). В силу непрерывности Д) существует lim v(t9 Д) = То есть в (5) существует производная дх/дц = и координаты tf. вектора v(t9 ц) удовлетво- ряют системе уравнений и начальным условиям (2). Теперь пусть ц меняется на интервале М.

Тогда правые части системы (2)

(и производные д/ди от них) непрерывны по (*,/*). По теореме 7 §7 решение системы (2), то есть производные тоже непрерывны по Дифференцнруемость решения по начальным условиям (следствие теоремы 1). Рассмотрим начальную задачу Пусть при (*,s) е D все функции Д и непрерывны, и на отрезке [t<912] Э t0 решение задачи (10) существует и проходит в области D. Тогда при существуют непрерывные производные решения £, по начальным условиям удовлетворяют системе Здесь решение задачи (10). Доказательство. Пусть xk0 = /х, а при t ^ fc ®f0 не зависит от Тогда система (10) удовлетворяет условиям теоремы 1.

Тогда решение x(t, ц) имеет непрерывные по t, ц производные по ц до порядка т включительно. Доказательство производится с помощью индукции по т. Для т = 1 утверждение теоремы 2 следует из теоремы 1. Пусть утверждение верно для производных до порядка 771 — 1 ^ 1. Докажем, что оно верно и для производных порядка т. Так как а функции и. = dxjdpi (i = 1. 7i) удовлетворяют системе (2), то надо проверить, что правые части в (2) имеют непрерывные производные по щ, fi до порядка т — 1 включительно.

1 по /i. Значйт, в (2) сложная функция принадлежит , аналогично dfjd^ также . По предположению индукции, примененному к системе (2), решение ир. ип системы (2) принадлежит по р. Так как ий =, то xt(t9 fi) G .

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Содержание

Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)
Производная функции, заданной параметрическим способом
Формула производной
Доказательство
Доказательство вторым способом
Производные высших порядков
Пример 1
Пример 2
Пример 3
Замечание
💡 Видео

Видео:Дифференциальные уравнения не разрешенные относительно производной | poporyadku.schoolСкачать

Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)

Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

Видео:14. Что такое параметрически заданная функция, производная параметрически заданной функции.Скачать

Производная функции, заданной параметрическим способом

Видео:#Дифуры I. Урок 10. Уравнения, не разрешённые относительно производной. Метод введения параметраСкачать

Формула производной

Пусть функция задана параметрическим способом:
(1)
где некоторая переменная, называемая параметром. И пусть функции и имеют производные при некотором значении переменной . Причем и функция имеет обратную функцию в некоторой окрестности точки . Тогда функция (1) имеет в точке производную , которая, в параметрическом виде, определяется по формулам:
(2)

Здесь и – производные функций и по переменной (параметру) . Их часто записывают в следующем виде:
;
.

Тогда систему (2) можно записать так:

Доказательство

По условию, функция имеет обратную функцию. Обозначим ее как
.
Тогда исходную функцию можно представить как сложную функцию:
.
Найдем ее производную, применяя правила дифференцирования сложной и обратной функций:
.

Доказательство вторым способом

Найдем производную вторым способом, исходя из определения производной функции в точке :
.
Введем обозначение:
.
Тогда и предыдущая формула принимает вид:
.

Воспользуемся тем, что функция имеет обратную функцию , в окрестности точки .
Введем обозначения:
; ;
; .
Разделим числитель и знаменатель дроби на :
.
При , . Тогда
.

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Производные высших порядков

Чтобы найти производные высших порядков, надо выполнять дифференцирование несколько раз. Допустим, нам надо найти производную второго порядка от функции, заданной параметрическим способом, следующего вида:
(1)

По формуле (2) находим первую производную, которая также определяется параметрическим способом:
(2)

Обозначим первую производную, посредством переменной :
.
Тогда, чтобы найти вторую производную от функции по переменной , нужно найти первую производную от функции по переменной . Зависимость переменной от переменной также задана параметрическим способом:
(3)
Сравнивая (3) с формулами (1) и (2), находим:

Теперь выразим результат через функции и . Для этого подставим и применим формулу производной дроби:
.
Тогда
.

Отсюда получаем вторую производную функции по переменной :

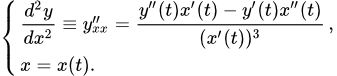
Она также задана в параметрическом виде. Заметим, что первую строку также можно записать следующим образом:
.

Продолжая процесс, можно получить производные функции от переменной третьего и более высоких порядков.

Заметим, что можно не вводить обозначение для производной . Можно записать так:
;
.

Видео:Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Пример 1

Найдите производную от функции, заданной параметрическим способом:

Видео:11. Производная неявной функции примерыСкачать

Пример 2

Найдите производную от функции, выраженной через параметр :

Раскроим скобки, применяя формулы для степенных функций и корней:
.

Находим производную . Для этого введем переменную и применим формулу производной сложной функции.

Находим искомую производную:
.

Видео:Не разрешенные относительно производной 1Скачать

Пример 3

Найдите производные второго и третьего порядков от функции, заданной параметрическим способом в примере 1:

В примере 1 мы нашли производную первого порядка:

Введем обозначение . Тогда функция является производной по . Она задана параметрическим способом:

Чтобы найти вторую производную по , нам надо найти первую производную по .

Дифференцируем по .
.
Производную по мы нашли в примере 1:
.
Производная второго порядка по равна производной первого порядка по :
.

Итак, мы нашли производную второго порядка по в параметрическом виде:

Теперь находим производную третьего порядка. Введем обозначение . Тогда нам нужно найти производную первого порядка от функции , которая задана параметрическим способом:

Производная третьего порядка по равна производной первого порядка по :
.