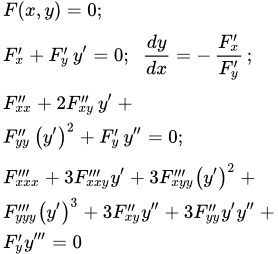Найти производную dy dx от неявной функции заданной уравнением

Неявная функция — это функция, например , заданная в виде уравнения:

F ( x , y ( x ) ) = 0

Как правило, вместо уравнения F ( x , y ( x ) ) = 0 пишут просто F ( x , y ) = 0 подразумевая, что есть функция от .

В качестве примера неявного задания функции, можно привести уравнение окружности:

уравнение декартового листа:

x 3 + y 3 = 3 ∙ a ∙ x ∙ y ( a = const ≠ 0 ) ,

и т.д. Все эти примеры можно записать в виде уравнения F ( x , y ) = 0 : уравнение окружности: F ( x , y ) = x 2 + y 2 − a 2 = 0 , уравнение декартового листа: F ( x , y ) = x 3 + y 3 − 3 ∙ a ∙ x ∙ y = 0 .

В связи с тем, что для исследования любой функции (в том числе и заданной неявно) необходимо вычислять производную, задача нахождения производной функции заданной неявно возникает довольно часто. Так, как же найти производную неявной функции? Исчерпывающий ответ на этот вопрос вы получите, воспользовавшись нашим онлайн калькулятором.
Для того, чтобы решить вашу задачу, для начала перепишите свою функцию в виде уравнения F ( x , y ) = 0 . Как это сделать, подробно описано выше (нужно просто перенести все слагаемые в левую часть уравнения, оставив справа ). Далее вам необходимо определиться, как у вас обозначается переменная и как обозначается функция, которая зависит от этой переменной. В приведенных выше примерах, — переменная, — функция, зависящая от .
Затем, вам необходимо ввести свое уравнение F ( x , y ) в наш онлайн калькулятор и получить решение вашей задачи.

Видео:11. Производная неявной функции примерыСкачать

Производная функции, заданной неявно

Видео:Производная неявной функцииСкачать

Производная первого порядка

Пусть функция задана неявным образом с помощью уравнения
(1) .
И пусть это уравнение, при некотором значении , имеет единственное решение . Пусть функция является дифференцируемой функцией в точке , причем
.
Тогда, при этом значении , существует производная , которая определяется по формуле:
(2) .

Доказательство

Для доказательства рассмотрим функцию как сложную функцию от переменной :
.
Применим правило дифференцирования сложной функции и найдем производную по переменной от левой и правой частей уравнения
(3) :
.
Поскольку производная от постоянной равна нулю и , то
(4) ;
.

Видео:11.1. Касательная к неявной функции / производная неявной функции ПРИМЕРЫСкачать

Производные высших порядков

Перепишем уравнение (4), используя другие обозначения:
(4) .
При этом и являются сложными функциями от переменной :
;
.
Зависимость определяет уравнение (1):
(1) .

Поскольку производная правой части уравнения (4) равна нулю, то
(5) .
Подставив сюда производную , получим значение производной второго порядка в неявном виде.

Дифференцируя, аналогичным образом, уравнение (5), мы получим уравнение, содержащее производную третьего порядка :
.
Подставив сюда найденные значения производных первого и второго порядков, найдем значение производной третьего порядка.

Продолжая дифференцирование, можно найти производную любого порядка.

Видео:Математика Без Ху!ни. Производная функции, заданной параметрически.Скачать

Примеры

Пример 1

Найдите производную первого порядка от функции, заданной неявно уравнением:
(П1) .

Решение по формуле 2

Находим производную по формуле (2):
(2) .

Перенесем все переменные в левую часть, чтобы уравнение приняло вид .
.
Отсюда .

Находим производную по , считая постоянной.
;
;
;
.

Находим производную по переменной , считая переменную постоянной.
;
;
;
.

По формуле (2) находим:
.

Мы можем упростить результат если заметим, что согласно исходному уравнению (П.1), . Подставим :
.
Умножим числитель и знаменатель на :
.

Решение вторым способом

Решим этот пример вторым способом. Для этого найдем производную по переменной левой и правой частей исходного уравнения (П1).

Подставим (из уравнения (П1)):
.
Умножим на :
.

Пример 2

Найти производную второго порядка от функции , заданной неявно с помощью уравнения:
(П2.1) .

Дифференцируем исходное уравнение, по переменной , считая что является функцией от :
;
.
Применяем формулу производной сложной функции.
.

Дифференцируем исходное уравнение (П2.1):
;
.
Из исходного уравнения (П2.1) следует, что . Подставим :
.
Раскрываем скобки и группируем члены:
;
(П2.2) .
Находим производную первого порядка:
(П2.3) .

Чтобы найти производную второго порядка, дифференцируем уравнение (П2.2).
;
;
;
.
Подставим выражение производной первого порядка (П2.3):
.
Умножим на :

;
.
Отсюда находим производную второго порядка.

Пример 3

Найти производную третьего порядка при от функции , заданной неявно с помощью уравнения:
(П3.1) .

Дифференцируем исходное уравнение по переменной считая, что является функцией от .
;
;
;
;
;
;
(П3.2) ;

Дифференцируем уравнение (П3.2) по переменной .
;
;
;
;
;
(П3.3) .

Из уравнений (П3.2), (П3.3) и (П3.4) находим значения производных при .
;
;
.

Автор: Олег Одинцов . Опубликовано: 16-02-2017

Видео:18+ Математика без Ху!ни. Производная неявной функции.Скачать

Математический портал

Видео:Первая и вторая производная неявной функцииСкачать

Nav view search

Navigation

Search

• Вы здесь:
• Home
• Математический анализ
• Дифференцирование сложных и неявно заданных функций.

Видео:27. Дифференцирование неявной функции двух переменныхСкачать

Дифференцирование сложных и неявно заданных функций.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Видео:14. Что такое параметрически заданная функция, производная параметрически заданной функции.Скачать

Сложные функции одной и нескольких независимых переменных.

Если $u=f(x_1, x_2, . x_n)-$ дифференцируемая функция переменных $x_1, x_2, . x_n,$ которые сами являются дифференцируемыми функциями независимой переменной $t:$ $$x_1=varphi_1(t),quad x_2=varphi_2(t),quad, x_n=varphi_n(t),$$ то производная сложной функции $u=f(varphi_1(t)),,varphi_2(t),, varphi_n(t))$ вычисляется по формуле $$frac

.$$ В частности , если $t$ совпадает , например , с переменной $x_1,$ то » полная » производная функции $u$ по $x_1$ равна $$frac=frac+fraccdotfrac+. +fraccdotfrac.$$ Пусть $u=f(x_1, x_2, . x_n),$ где $$x_1=varphi_1(t_1, t_2, . t_m),quad x_2=varphi_2(t_1, t_2, . t_m),quad, x_n=varphi_n(t_1, t_2, . t_m),$$ $(t_1, t_2. t_m) -$ независимые переменные. Частные производные функции $u$ по $t_1, t_2, . t_m$ выражаются следующим образом: $$frac=fraccdotfrac+fraccdotfrac+. +fraccdotfrac,$$ $$frac=fraccdotfrac+fraccdotfrac+. +fraccdotfrac,$$ $$cdots$$ $$frac=fraccdotfrac+fraccdotfrac+. +fraccdotfrac.$$При этом выражение для дифференциала 1-го порядка сохраняет свой вид $$du=fracdx_1+fracdx_2+. +fracdx_n.$$ Выражения для дифференциалов высших порядков сложной функции , вообще говоря , отличаются от выражения вида $$d^mu=left(fracdx_1+fracdx_2+. +fracdx_nright)^mu.$$ Например , дифференциал 2- го порядка выражается формулой

Видео:Производная функции заданной неявноСкачать

Неявные функции одной и нескольких независимых переменных.

Пусть уравнение $f(x, y)=0,$ где $f-$ дифференцируемая функция переменных $x$ и $y$ определяет $y$ как функцию $x.$ Первая производная этой неявной функции $y=y(x)$ в точке $x_0$ выражается по формуле $$left.fracright|_=-fracqquadqquadqquad(1)$$ при условии, что $f’_y(x_0, y_0)neq 0,$ где $y_0=y(x_0), f(x_0, y_0)=0.$

Производные высших порядков вычисляются последовательным дифференцированием формулы (1).

Примеры:

7.114. Найти $frac

,$ если $z=x^y,$ где $x=ln t, ,, y=sin t.$

Решение.

Найдем частные производные:

7.118. Найти $frac$ и $frac,$ если $z=ln(e^x+e^y),$ где $ y=fracx^3+x.$

Решение.

Решение.

Найдем частные производные:

7.125. Найти $dz,$ если $z=f(u, v),$ где $ u=sinfrac,, v=sqrt.$

Решение.

Найдем частные производные:

7.138. Найти $d^2u,$ если $u=f(ax,by,cz).$

Решение.

Обозначим $$x_1=ax,$$ $$x_2=by,$$ $$x_3=cz.$$ Будем пользоваться формулой

Решение.

Найдем частные производные

Решение.

Производную$frac$ ищем по формуле $$frac=-frac.$$ Здесь $f(x,y)=x-y+arctg y.$

Найдем частные производные

Производную второго порядка $frac$ находим, дифференцируя выражение $frac=frac$ по переменной $x.$

Решение.

Найдем частные производные

Производные второго порядка находим, дифференцируя найденные производные первого порядка по соответствующим переменным.

🎥 Видео

32. Второй дифференциал неявной функции примерыСкачать

Как находить производную неявной функции - bezbotvyСкачать

28. Частные производные неявной функции. примерСкачать

19. Производная второго порядка неявной функцииСкачать

Производные №4 Производная неявной функцииСкачать

29. Частные производные и дифференциал функции заданной неявно. примерСкачать

11.2 Найти производную неявной функции /ПРИМЕРЫСкачать

24. Вычисление дифференциала. Дифференциал неявной функцииСкачать

Математический анализ, 31 урок, Дифференцирование сложных и неявных функцийСкачать

20. Вторая производная параметрической функции, вывод формулы, примерСкачать