Найти произведение корней характеристического уравнения для лоду y 4y 5y

Условие

Решение

Общее решение неоднородного дифферециального уравнения второго порядка у=у₀+Y
Где
у₀- частное решение однородного уравнения
y»+4y’+5y=0
Y- частное решение неоднородного уравнения

Составляем характеристическое уравнение
однородного уравнения:
k²+4k+5=0
D=16-20=-4
корни комплексно-сопряженные
-2+i и -2 -i
α=-2 β=1
y₀=e^(-2x)(C₁cosx+C₂sinx)

Y=ax+b — частное решение находим в виде, подобном правой части. Справа линейная функция
Y`=a
Y«=0
Подставляем в данное уравнение
0+4а+5(ax+b)=25x
5ax+(4a+5b)=25x
5a=25
a=5
4a+b=0
b=-4a=-20
Общее решение данного неоднородного уравнения
у=e^(-2x)(C₁cosx+C₂sinx)+5x-20
Находим частное решение данного неоднородного из условия
y(0)=2 y'(0)=0
Находим
y`=e^(-2x)*(-2x)`*(C₁cosx+C₂sinx)+e^(-2x)*(-C₁sinx+C₂cosx)+5=e^(-2x)*(-2C₁cosx-2C₂sinx-C₁sinx+C₂cosx)+5

Составляем систему:
2=e^(0)(C₁cos0+C₂sin0)+5*0-20
0=e^(0)*(-2C₁cos0-2C₂sin0-C₁sin0+C₂cos0)+5

О т в е т.
Общее решение:
у=e^(-2x)(C₁cosx+C₂sinx)+5x-20
Частное решение
у=у=e^(-2x)(22cosx+39sinx)+5x-20

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Линейные дифференциальные уравнения с постоянными коэффициентами

Линейное дифференциальное уравнение (*) назовём уравнением с постоянными коэффициентами, если в этом уравнении коэффициенты постоянны, то есть a_i(x)=const. Тогда соответствующее однородное уравнение L(y)=0 будет иметь вид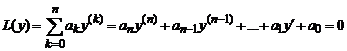
. (6)
Решение уравнения (6) будем искать в виде y = e rx . Тогда y’ = r·e rx , y» = r 2 ·e rx ,…, y ( n ) = r n ·e rx . Подставляя в (6), получаем

Пример №1 . Для уравнения y»-3y’ + 2y=0 корни характеристического уравнения r 2 — 3r + 2 = 0 равны r₁ = 1, r₂ = 2 (корни были найдены через сервис нахождения дискриминанта). Следовательно, фундаментальную систему решений составляют функции y₁ = e x , y₂ = e 2 x , а общее решение записывается в виде y = C₁e x + C₂e 2 x .
2. Среди корней характеристического уравнения есть кратные. Предположим, что r₁ имеет кратность α, а все остальные различны. Рассмотрим вначале случай r₁ = 0. Тогда характеристическое уравнение имеет вид:
a_n(x)·r n +a_n-1(x)·r n-1 + . + a_n-α(x)·r α =0
так как в противном случае r не являлось бы корнем кратности α. Следовательно, дифференциальное уравнение имеет вид:
a_n(x)·y (n) +a_n-1(x)·y (n-1) + . + a_n-α(x)·y α =0
то есть не содержит производных порядка ниже α. Этому уравнению удовлетворяют все функции, у которых производные порядка α и выше равны нулю. В частности, таковыми являются все полиномы степени не выше α-1, например,
1, x, x 2 , …, x α-1 . (9)
Покажем, что данная система линейно независима. Составив определитель Вронского этой системы функций, получим

Пример №2 . Для уравнения y»’-4y»+4y’ = 0 характеристическое уравнение r 3 -4r 2 + 4r = 0 имеет корни r=0 кратности 1 и r=2 кратности 2, так как r 3 -4r 2 + 4r = r(r-2) 2 , поэтому фундаментальной системой решений исходного уравнения является система функций y₁ = 1, y₂ = e 2 x , y₃ = xe 2 x , а общее решение имеет вид y = C₁ + C₂e 2 x + C₃xe 2 x .
3. Среди корней характеристического уравнения есть комплексные корни. Можно рассматривать комплексные решения, но для уравнений с действительными коэффициентами это не очень удобно. Найдём действительные решения, соответствующие комплексным корням. Так как мы рассматриваем уравнение с действительными коэффициентами, то для каждого комплексного корня r_j = a+bi кратности α характеристического уравнения комплексно сопряжённое ему число r_k = a-bi также является корнем кратности α этого уравнения. Соответствующими этим корням парами решений являются функции y_j l =x l ·e (a+b·i)x и y_k l =x l ·e (a-b·i)x , l=0,1. α-1. Вместо этих решений рассмотрим их линейные комбинации

Видео:ЛОДУ с постоянными коэффициентами, корни характеристического уравнения | Лекция 37 | МатанализСкачать

Задача Коши онлайн

Данная задача возникает при поиске частного решения дифференциального уравнения. Наш онлайн калькулятор, построенные на основе системы Wolfram Alpha, позволяет найти решение задачи Коши для различных типов дифференциальных уравнений. Чтобы начать работу, необходимо ввести данные своей задачи (дифференциальное уравнение и начальные условия) в калькулятор.

Найти решение задачи Коши для дифференциального уравнения:

при заданных начальных условиях:

При постановке задачи Коши, указываются так называемые начальные условия, позволяющие однозначно выделить искомое частное решение из общего. Эти условия включают в себя значения функции и всех её производных до включительно (где -порядок дифференциального уравнения), заданные в одной и той же точке .

Поясним вышесказанное на конкретном примере. Пусть нам требуется найти частное решение дифференциального уравнения:

удовлетворяющее начальным условиям:

Первым делом, используя различные методы (Бернули, вариации произвольной постоянной Лагранжа), сначала находим общее решение данного дифференциального уравнения:

Теперь, для поиска частного решения, нам необходимо использовать заданные начальные условия. Для этого, находим производную функции полученной ранее:

Далее, поставляем начальные условия в функцию и её производную :

Решая полученную систему уравнений получаем значения произвольных постоянных и :

Подставляем полученные результаты в общее решение дифференциального уравнения, в результате получаем искомое частное решение:

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Другие полезные разделы:

Видео:Линейное дифференциальное уравнение Коши-ЭйлераСкачать

Оставить свой комментарий:

Мы в социальных сетях:
Группа ВКонтакте | Бот в Телеграмме

🔍 Видео

Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентамСкачать

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Характеристическое уравнение в ДУСкачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Найти значение суммы и произведения корней квадратного уравненияСкачать

ЛОДУ с постоянными коэффициентами | Лекция 15 | МатАн | СтримСкачать

15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Решение системы дифференциальных уравнений методом ЭйлераСкачать

ДУ Линейные уравнения с постоянными коэффициентамиСкачать

Определяем тип ДУ 1Скачать

Однородное линейное дифференциальное уравнение. Алгоритм решенияСкачать

УРАВНЕНИЕ 4 КЛАСС МАТЕМАТИКА УЧИМСЯ РЕШАТЬ УРАВНЕНИЯ МЕТОДИКА ОБУЧЕНИЯ РЕШАЕМ УРАВНЕНИЯ #уравнениеСкачать

13. Как решить дифференциальное уравнение первого порядка?Скачать

Видеоурок "Нахождение частных решений по виду правой части"Скачать