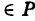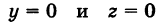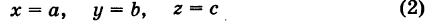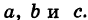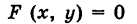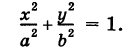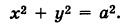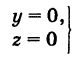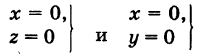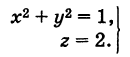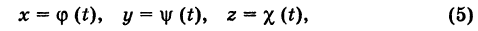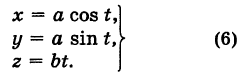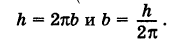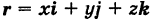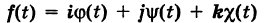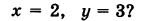Найти поверхность удовлетворяющую данному уравнению и проходящую через данную линию

Найдём первый интеграл системы (1)

— первый интеграл (2)

Найдём второй интеграл системы (1)

— второй интеграл (3)

Из полученных интегралов можно составить общее решение квазилинейного дифференциального уравнения первого порядка

Найдём частное решение при заданных линиях. Для этого составим систему из полученных интегралов (2), (3) и условий

(вместо y в (2), (3) подставим 1, а вместо x подставим z)

— полученная завязка и является частным решением уравнения

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Вывод

В данной курсовой работе описано квазилинейное уравнение первого порядка в частных производных, а так же его многомерный случай и методы нахождения общего решения этого уравнения.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Уравнения поверхности и линии в пространстве с примерами решения

Содержание:

Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Уравнения поверхности и линии в пространстве

Определение: Уравнение м поверхности в пространстве Oxyz называется такое уравнение между переменными х, у у z, которому удовлетворяют координаты всех точек данной поверхности и не удовлетворяют координаты точек, не лежащих на этой поверхности. То есть если

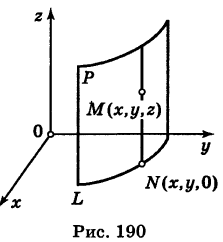
— уравнение поверхности Р (рис. 189), то при М(х, у, z)

Таким образом, уравнение (1) выполнено тогда и только тогда, когда точка М(х, у, z) принадлежит данной поверхности. Координаты произвольной точки поверхности называются текущими координатами точки. Поэтому составить уравнение поверхности — это значит найти связь между текущими координатами ее точек.

Пример (уравнения координатных плоскостей):

Каждая точка М(х, у, z), лежащая на координатной плоскости Oyz, имеет абсциссу х = 0; обратно, если для какой-нибудь точки М(х, у, z) абсцисса ее х = 0, то эта точка расположена на плоскости Oyz. Следовательно,

— уравнение координатной плоскости Oyz. Аналогично,

— соответственно уравнения координатных плоскостей Oxz и Оху.

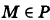
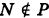
Формула обозначает, что точка М принадлежит Р. Формула обозначает, что точка N не принадлежит Р.

В более общем случае

— уравнения трех плоскостей, перпендикулярных соответствующим координатным осям Ох, Оу, Ог и отсекающих на них отрезки, численно равные

Теорема: Уравнение цилиндрической поверхности, образующие которой параллельны координатной оси, не содержит текущей координаты, одноименной с этой координатной осью, и обратно.

Доказательство: Пусть, например, цилиндрическая поверхность Р образована перемещением прямой 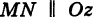(образующая) вдоль заданной линии L, лежащей в плоскости Оху (направляющая) (рис. 190).

Обозначим через М(х, у, z) точку поверхности Р с текущими координатами х, у и z. Образующая MN, проходящая через точку М, пересекает направляющую, очевидно, в точке N(x, у, 0).

— уравнение направляющей L в координатной плоскости Оху. Этому уравнению удовлетворяют координаты точки N. Так как точка М поверхности Р имеет ту же самую абсциссу хиту же самую ординату у, что и точка N, а переменная г в уравнение (3) не входит, то координаты точки М также удовлетворяют уравнению (3). Таким образом, координаты любой точки М(х, у, z) поверхности Р удовлетворяют уравнению (3). Обратно, если координаты какой-нибудь точки М(х, у, z) удовлетворяют уравнению (3), то эта точка расположена на прямой MN || Оz такой, что ее след на плоскости Оху, точка N(x, у, 0), лежит на линии L, а значит, точка М принадлежит цилиндрической поверхности Р. Следовательно,

является уравнением цилиндрической поверхности в пространстве Oxyz, причем в этом уравнении отсутствует координата z.

Пример (уравнение эллиптического цилиндра):

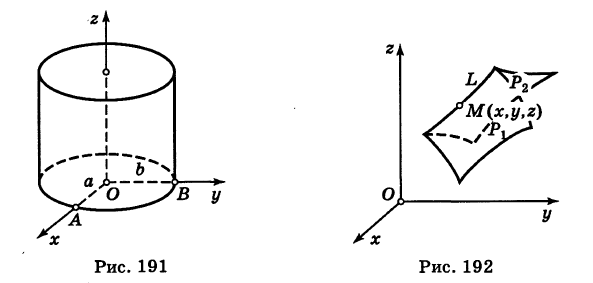
Эллиптический цилиндр, в основании которого лежит эллипс с полуосями а и b, а осью служит ось Оz (рис. 191), на основании предыдущей теоремы имеет уравнение

В частности, при а = b получаем уравнение кругового цилиндра

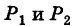
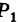
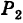
Линию L в пространстве можно задать как пересечение двух данных поверхностей (рис. 192). Точка , лежащая на линии L, принадлежит как поверхности так и поверхности , и, следовательно, координаты этой точки удовлетворяют уравнениям обеих поверхностей.

Поэтому под уравнениями линии в пространстве понимается совокупность двух уравнений:

являющихся уравнениями поверхностей, определяющих данную линию.

Не нужно думать, что для нахождения уравнений линий систему (4) следует «решить». Этого, вообще говоря, нельзя сделать, так как число уравнений системы (4) меньше числа неизвестных. Точный смысл, который придается равенствам (4), следующий: линии L принадлежат те и только те точки , координаты которых удовлетворяют обоим уравнениям системы (4).

Заметим, что данную линию можно по-разному задавать как пересечение поверхностей. Поэтому линии в пространстве соответствует бесчисленное множество равносильных между собой систем уравнений.

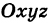
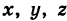
Определение: Уравнениями линии в пространстве называется такая пара уравнений между переменными , которой удовлетворяют координаты каждой точки, лежащей на данной линии, и не удовлетворяют координаты любой точки, не лежащей на этой линии.

Пример (уравнения координатных осей):

Ось Ох можно, рассматривать как пересечение координатных плоскостей Оху и Oxz. Поэтому

— уравнения оси Ох. Аналогично,

— уравнения осей Оу и Oz соответственно.

Пример:

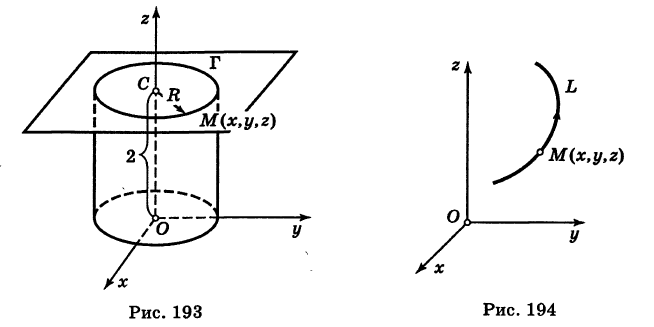
Написать уравнения окружности Г радиуса R = 1, центр которой находится в точке С(0, 0, 2) и плоскость которой параллельна координатной плоскости Оху (рис. 193).

Решение:

Окружность Г можно рассматривать как пересечение кругового цилиндра радиуса 1 с осью Oz и горизонтальной плоскости, расположенной выше координатной плоскости Оху на две единицы. Поэтому уравнения данной окружности есть

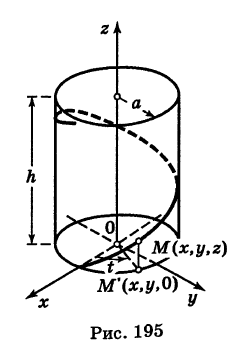
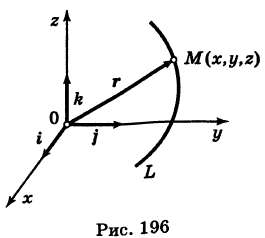
В механике линию L часто рассматривают как след движущейся точки (рис. 194). Пусть х, у, z — текущие координаты точки М линии L. Так как с течением времени точка М перемещается и ее координаты меняются, то они являются функциями времени t. Следовательно, имеем

где 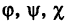— некоторые определенные функции. Обобщая уравнения (5), под t понимают вспомогательную переменную (параметр)> не обязательно время; поэтому уравнения (5) носят название параметрических уравнений линии в пространстве.

Исключая из уравнений (5) параметр t, мы получим два соотношения между текущими координатами х, у и z, которые представляют собой уравнения некоторых поверхностей, проходящих через данную линию.

Пример:

Написать уравнения винтовой линии радиуса а и шага 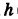(рис. 195).

Решение:

Пусть М (х, у, z) — текущая точка винтовой линии, М’ (х, у, 0) — ее проекция на плоскость Оху.

Приняв за параметр 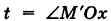и учитывая, что аппликата г винтовой линии растет пропорционально углу поворота t, будем иметь

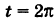
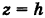
Для определения коэффициента пропорциональности b положим ; тогда . Следовательно,

Исключая параметр t из первого и второго, а также из первого и третьего уравнений (6), получаем

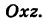
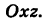
Следовательно, винтовая линия представляет собой пересечение кругового цилиндра с образующими, параллельными оси Oz, и цилиндрической поверхности с образующими, параллельными оси Оу, и имеющей своей направляющей косинусоиду, лежащую в плоскости . Из уравнений (6′) также вытекает, что проекция винтовой линии (6′) на координатную плоскость Оху есть окружность, а на координатную плоскость — косинусоида.

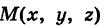
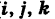
Текущую точку кривой L можно характеризовать ее радиусом-вектором («следящий радиус-вектор») (рис. 196)

( — орты). Тогда из (5) получаем векторное уравнение линии

— так называемая вектор-функция скалярного аргумента t.

В механике в качестве параметра t обычно берут время. В таком случае линию (7) называют траекторией точки М(х, у, z).

Множество всех точек М(х, у, г) пространства, координаты которых удовлетворяют данному уравнению (или системе уравнений), называется геометрическим образом (графиком) данного уравнения (или системы уравнений).

Пример:

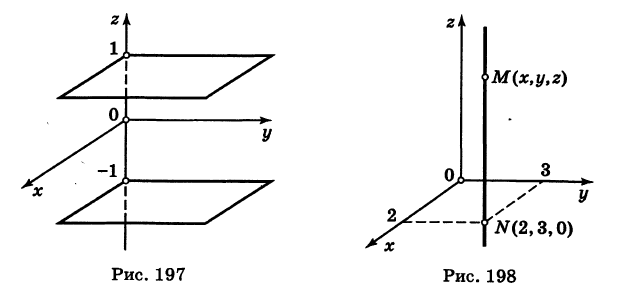
Какой геометрический образ соответствует уравнению

Решение:

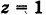
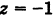
Из уравнения (8) получаем или . Следовательно, графиком уравнения (8) является пара плоскостей, параллельных координатной плоскости Оху и отстоящих от нее на расстояниях, равных единице (рис. 197).

Пример:

Какой геометрический образ соответствует паре уравнений

Решение:

Искомый график представляет собой пересечение плоскостей х = 2 и у = 3 и, следовательно, является прямой линией, параллельной оси Oz и имеющей след N (2, 3, 0) на координатной плоскости Оху (рис. 198).

• Общее уравнение плоскости
• Угол между плоскостями
• Понятие о производной вектор-функции
• Криволинейные интегралы
• Прямоугольная система координат на плоскости и ее применение
• Линии второго порядка
• Полярные координаты
• Непрерывность функции

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:11. Прямая в пространстве и ее уравненияСкачать

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Поверхности. Касательная плоскость и нормаль

Видео:Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать

Краткие теоретические сведения

Способы задания поверхностей

Рассматриваем вектор–функцию двух скалярных аргументов: $$vec=vec(u,v).$$ Годографом такой функции является поверхность.

Запишем четыре способа задания поверхности: 1. Векторное уравнение: $$vec=vec(u,v).$$ 2. Параметрическое уравнение: $$x=x(u,v),,, y=y(u,v),,, z=z(u,v).$$ 3. Неявное уравнение: $$varPhi(x,y,z)=0.$$ 4. Явное уравнение: $$z=z(x,y).$$

Поверхность называется регулярной ($k$ раз дифференцируемой), если у каждой точки этой поверхности есть окрестность, допускающая регулярную параметризацию (то есть функции $x(u,v), y(u,v),z=z(u,v)$ $k$ раз непрерывно дифференцируемы). При $k=1$ поверхность называется гладкой.

Регулярная поверхность в окрестности каждой своей точки допускает бесчисленное множество параметризаций.

Кривая, лежащая на поверхности $vec=vec(u,v)$, задается уравнениями $$ u=u(t),,, v=v(t).$$ Линии $u=mbox$, $v=mbox$ являются координатными линиями данной параметризации поверхности.

Видео:Уравнения прямой на плоскости | Векторная алгебраСкачать

Решение задач

Задача 1 (Феденко №544)

Дана поверхность begin x=u+v, ,, y=u-v,,, z=uv. end Проверить, принадлежат ли ей точки $A(4,2,3)$ и $B(1,4,-2)$.

Ответ. Точка $A$ принадлежит, так как ее координаты удовлетворяют системе уравнений, задающих поверхность. Точка $B$ не принадлежит поверхности.

Задача 2 (Феденко № 546)

Найдите неявное уравнение поверхности, заданной параметрическими уравнениями: begin begin x & = x_0 + a,mbox,u,mbox,v, \ y & = y_0 + b,mbox,u,mbox,v, \ z & = z_0 + c,mbox,u. end end

Ответ. Эллипсоид с полуосями $a$, $b$, $c$ и центром в точке $(x_0, y_0, z_0)$: begin frac+frac+frac=1. end

Задача 3 (Феденко №528)

В плоскости $xOz$ задана кривая $x=f(u)$, $z=g(u)$, не пересекающая ось $Oz$. Найдите параметризацию поверхности, полученной при вращении этой кривой вокруг оси $Oz$.

Решение задачи 3

Произвольная точка $M$, принадлежащая кривой и имеющая координаты $x_0=f(u_0)$, $y_0=0$, $z_0=g(u_0)$, движется по окружности с центром на оси $Oz$ и радиусом $R=f(u_0)$ в плоскости, параллельной плоскости $xOy$: $z=g(u_0)$. Поэтому изменение ее координат можно записать следующими уравнениями: begin left< begin x_0 & = & f(u_0),mbox,v, \ y_0 & = & f(u_0),mbox,v, \ z_0 & = & g(u_0). \ end right. end

Поскольку точка $M$ произвольная, уравнение искомой поверхности: begin left< begin x & = & f(u),mbox,v, \ y & = & f(u),mbox,v, \ z & = & g(u). \ end right. end

Видео:12. Уравнения прямой в пространстве Решение задачСкачать

Касательная плоскость. Нормаль

Видео:Поверхности второго порядкаСкачать

Краткие теоретические сведения

Пусть $vec=vec(u,v)in C^1$ — поверхность, проходящая через точку $P(u_0, v_0)$. Пусть $u=u(t)$, $v=v(t)$ — уравнения гладкой кривой, проходящей через точку $P(u_0, v_0)$ и лежащей на заданной поверхности.

Пусть точка $P$ не является особой, то есть ранг матрицы begin left( begin x_u & y_u & z_u \ x_v & y_v & z_v \ end right) end в точке $P$ равен $2$ (для особой точки ранг меньше $2$). Если поверхность задана неявно $varPhi(x,y,z)=0$, то в не особой точке $P$ выполняется условие: $varPhi_x^2+varPhi_y^2+varPhi_z^2neq0.$

Касательная к кривой $u=u(t)$, $v=v(t)$ на поверхности $vec=vec(u,v)$ определяется вектором: begin displaystylefrac<dvec>

$ лежат в одной плоскости, определяемой векторами $vec_u$, $vec_v$. Эта плоскость называется касательной плоскостью к поверхности в точке $P$. Запишем уравнение касательной плоскости.

Обозначения:
— $vec=$ — радиус-вектор произвольной точки касательной плоскости.
— $vec=$ — радиус вектор точки $P(u_0, v_0)$.
— Частные производные $x_u$, $y_u$, $z_u$, $x_v$, $y_v$, $z_v$ вычисляются в точке $P(u_0, v_0)$.

Уравнение касательной плоскости:

1. Если поверхность задана векторно, то уравнение касательной плоскости можно записать через смешанное произведение трех линейно зависимых векторов: $$ left(vec-vec, , vec_u, , vec_v right)=0. $$ 2. Если поверхность задана параметрически, запишем определитель: begin left| begin X-x & Y-y & Z-z \ x_u & y_u & z_u\ x_v & y_v & z_v\ end right|=0 end 3. Если поверхность задана неявным уравнением: begin varPhi_x(X-x)+varPhi_y(Y-y)+varPhi_z(Z-z)=0. end 4. В случая явного задания поверхности, уравнение касательной плоскости примет вид: begin (Z-z)=z_x(X-x)+z_y(Y-y). end

Нормалью поверхности в точке $P$ называется прямая, проходящая через $P$ перпендикулярно касательной плоскости в этой точке.

Уравнение нормали:

1.$$ vec=vec + lambdavec, ,, vec=vec_utimesvec_v. $$ 2. begin displaystylefrac< left| begin y_u & z_u\ y_v & z_v\ end right|>= displaystylefrac< left| begin z_u & x_u\ z_v & x_v\ end right|>= displaystylefrac< left| begin x_u & y_u\ x_v & y_v\ end right|>. end 3. begin displaystylefrac=displaystylefrac=displaystylefrac. end 4. begin displaystylefrac=displaystylefrac=displaystylefrac. end

Видео:Найти поток векторного поля через замкнутую поверхность S (нормаль внешняя).Скачать

Решение задач

Задача 1 (Феденко №574)

Дана поверхность begin x=u,mbox,v,,, y=u,mbox,v,,, z=u. end Написать:
а) уравнение касательной плоскости к поверхности;
б] уравнение нормали к поверхности;
в) касательной к линии $u=2$
в точке $Mleft(u=2, v=displaystylefracright)$ поверхности.

Задача 2

Через точки $A(0,1,0)$ и $B(1,0,0)$ провести плоскость, касательную к поверхности $vec=$.

Ответ. $z=0, -2X-2Y+Z+2=0$.

Задача 3

Построить касательную плоскость к поверхности $y=x^2+z^2$, перпендикулярную вектору $vec$.

Задача 4

Через точку $M(1,2,1)$ провести плоскость, касательную к поверхности $x^2+y^2-z^2=0$.

Ответ. $X-Z=0$, $3X-4Y+5Z=0$.

Задача 5 (Феденко №594)

Докажите, что поверхности begin z=mbox(xy), ,, x^2-y^2=a end ортогональны в точках их пересечения.

Решение задачи 5

Запишем направляющие векторы нормалей к поверхностям, проведенным в точках их пересечения: begin begin vec_1&=left<frac<mbox^2(x_0y_0)>,frac<mbox^2(x_0y_0)>,-1right>,\ vec_2&=left. end end Скалярные произведения векторов $n_1$ и $n_2$ равны нулю, следовательно векторы ортогональны. begin n_1cdot n_2=0. end

Видео:УРАВНЕНИЕ ПРЯМОЙ на плоскости 8 и 9 классСкачать

Решение дифференциальных уравнений на заказ

Мы решаем задачи по обыкновенным дифференциальным уравнениям, включая системы уравнений и исследование на устойчивость. Также решаем дифференциальные уравнения в частных производных первого порядка. Все задачи решаем с объяснениями в рукописном виде.

Чтобы заказать работу, перейдите по этой ссылке, и заполните форму.
Через 10-15 минут вам поступят предложения с указанием цены. Подробно расписанный пример дальнейших действий можно прочитать на странице «Как купить решение задач (пошаговая инструкция)».

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Цены за решение задач

Цена решения одного обыкновенного дифференциального уравнения зависит от его сложности и составляет от 50 до 150 рублей. Стоимость также зависит от времени года. Во время сессий (декабрь, январь, май и июнь) – дороже. В остальное время – дешевле.

Видео:Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Примеры решений задач

На этом сайте, в разделе «Дифференциальные уравнения», рассмотрены практически все основные методы решения обыкновенных дифференциальных уравнений. Почти каждая страница содержит описание вида уравнения, метод его решения и подробно разобранный пример.

Ниже приводятся примеры решений задач в том виде, в котором его получают клиенты.

Найти общее решение уравнения и решить задачу Коши с указанным начальным условием.
1) ,
при .
2)
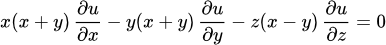
при .

Найти поверхность, удовлетворяющую данному уравнению и проходящую через данную линию.
,
.
Скачать решение задачи >>>

Видео:Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать

Будьте осторожны

Заказывая решения задач, будьте осторожны! Если вы учитесь на бухгалтера (или точно знаете, что ваша работа не будет связана с дифференциальными уравнениями) и вам нужно сдать реферат, контрольную работу или курсовую по дифференциальным уравнениям, то можете смело заказать его написание в специализированных компаниях. Сэкономленное время можно потратить на более глубокое изучение тех предметов, которые вам пригодятся в дальнейшей работе.

Но если ваша специальность тесно связана с математикой, то приложите все усилия, чтобы выполнить работу самостоятельно. Только если вы научились решать уравнения самостоятельно и хотите глубже разобраться в других нужных вам предметах, то можно сэкономить время, заказав выполнение работы у других лиц.

🎬 Видео

Поверхности и линии уровняСкачать

Уравнение прямой на плоскости. Решение задачСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

§8.1 Общее уравнение прямой на плоскостиСкачать

ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать