Полный дифференциал для функции двух переменных:
- Примеры
≡ x^2/(x+2)
cos 2 (2x+π) ≡ (cos(2*x+pi))^2≡ x+(x-1)^(2/3)
Пусть f(x) дифференцируема в точке x0 и f ‘(x0)≠0 , тогда ∆y=f’(x0)∆x + α∆x, где α= α(∆x) →0 при ∆x→0. Величина ∆y и каждое слагаемое правой части являются бесконечно малыми величинами при ∆x→0. Сравним их: 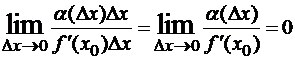
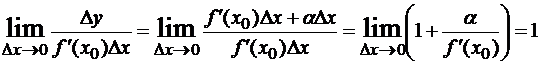
f’(x0)∆x. Следовательно, f’(x0)∆x представляет собой главную и вместе с тем линейную относительно ∆x часть приращения ∆y (линейная – значит содержащая ∆x в первой степени). Это слагаемое называют дифференциалом функции y=f(x) в точке x0 и обозначают dy(x0) или df(x0). Итак, для произвольных значений x
dy=f′(x)∆x. (1)
Полагают dx=∆x, тогда
dy=f′(x)dx. (2)
Пример . Найти производные и дифференциалы данных функций.
а) y=4 tg2 x
Решение:
дифференциал:
б)
Решение:
дифференциал:
в) y=arcsin 2 (lnx)
Решение:
дифференциал:
г)
Решение:

дифференциал:
Пример . Для функции y=x 3 найти выражение для ∆y и dy при некоторых значениях x и ∆x.
Решение. ∆y = (x+∆x) 3 – x 3 = x 3 + 3x 2 ∆x +3x∆x 2 + ∆x 3 – x 3 = 3x 2 ∆x+3x∆x 2 +∆x 3 ; dy=3x 2 ∆x (взяли главную линейную относительно ∆x часть ∆y). В данном случае α(∆x)∆x = 3x∆x 2 + ∆x 3 .
Видео:Математический анализ, 30 урок, Полный дифференциалСкачать

Дифференциал функции онлайн
Дифференциалом функции называется главная (линейная по ) часть приращения функции. Чтобы понять данное определение, рассмотрим следующий рисунок.
На рисунке изображён график функции и касательной к ней в точке . Дадим аргументу функции некоторое приращение , тогда функция также получит некоторое приращение . Величина называется дифференциалом функции . При этом, из графика следует, что равно приращению ординаты касательной, проведённой в точке к функции . Именно поэтому дифференциалом называют линейную часть приращения функции, т.е. приращение ординаты касательной.
Из рисунка следует, что угол наклона касательной , который она образует с положительным направлением оси и — равны. Кроме того, тангенс угла наклона касательной равен значению производной функции в точке касания:
Из треугольника следует, что:
Таким образом, дифференциал функции выражается следующей формулой:
Рассмотрим ещё такой момент: из рисунка следует, что , причем . Причем, чем меньше , тем меньший вклад в величину вносит значение . Т.е. при достаточно малых значениях , можно считать, что . Данное соотношение позволяет вычислять приближенное значение функции в точке , если известно её значение в точке .
Дифференциал высшего порядка (например порядка ) определяется как дифференциал от дифференциала -ого порядка:
Например, дифференциал второго порядка вычисляется следующим образом:
Аналогичным образом получаем формулу для вычисления дифференциала -ого порядка:
где — -ая производная функции по переменной .
Пару слов стоит сказать о вычислении дифференциала функции многих переменных, который в этом случае называется полным дифференциалом. Полный дифференциал функции, зависящей от -переменных определяется по формуле:
Выражения для дифференциалов высших порядков функции многих переменных можно получить исходя из общей формулы:
В общем случае, для возведения суммы в -ую степень необходимо воспользоваться формулой бинома Ньютона. Рассмотрим процесс получения формулы полного дифференциала второго порядка функции двух переменных:
Наш онлайн калькулятор способен вычислить дифференциалы разных порядков для любых функций одной или нескольких переменных с описанием подробного решения на русском языке.
Видео:25. Как найти дифференциал второго порядка функции двух переменных (часть 2)Скачать

Полное приращение и полный дифференциал
Вы будете перенаправлены на Автор24
Если для каждой пары $(x,y)$ значений двух независимых переменных из некоторой области ставится в соответствие определенное значение $z$, то говорят, что $z$ является функцией двух переменных $(x,y)$. Обозначение: $z=f(x,y)$.
В отношении функции $z=f(x,y)$ рассмотрим понятия общего (полного) приращения функции и полного дифференциала.
Пусть дана функция $z=f(x,y)$двух независимых переменных $(x,y)$.
Если аргументу $x$ дать приращение $Delta x$, а аргументу $y$ — приращение $Delta y$, то получается полное приращение заданной функции $z=f(x,y)$. Обозначение:
Записать полное приращение заданной функции
Решение:
По определению полного приращения некоторой функции найдем:
Вычислить полное приращение заданной функции $z=xy$ в точке $(1;2)$ при $Delta x=0,1;, , Delta y=0,1$.
Решение:
По определению полного приращения некоторой функции найдем:
$Delta z=(x+Delta x)cdot (y+Delta y)$ — полное приращение функции $z=f(x,y)$.
[Delta z=(1+0,1)cdot (2+0,1)=1,1cdot 2,1=2,31.]
Если для каждой тройки $(x,y,z)$ значений трех независимых переменных из некоторой области ставится в соответствие определенное значение $w$, то говорят, что $w$ является функцией трех переменных $(x,y,z)$ в данной области.
Если для каждой совокупности $(x,y,z. t)$ значений независимых переменных из некоторой области ставится в соответствие определенное значение $w$, то говорят, что $w$ является функцией переменных $(x,y,z. t)$ в данной области.
Готовые работы на аналогичную тему
Для функции трех и более переменных, аналогично как для функции двух переменных определяются полное приращение:
Записать полное приращение заданной функции
Решение:
По определению полного приращения некоторой функции найдем:
$Delta w=((x+Delta x)+(y+Delta y))cdot (z+Delta z)$ — полное приращение функции $w=f(x,y,z)$.
Вычислить полное приращение заданной функции $w=xyz$ в точке $(1;2;1)$ при $Delta x=0,1;, , Delta y=0,1;, , Delta z=0,1$.
Решение:
По определению полного приращения некоторой функции найдем:
$Delta w=(x+Delta x)cdot (y+Delta y)cdot (z+Delta z)$ — полное приращение функции $w=f(x,y,z)$.
[Delta z=(1+0,1)cdot (2+0,1)cdot (1+0,1)=1,1cdot 2,1cdot 1,1=2,541.]
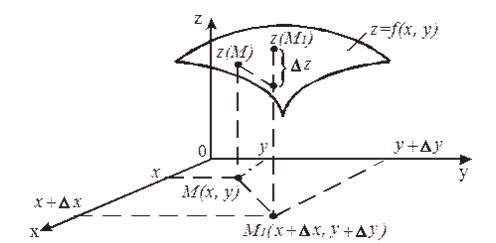
С геометрической точки зрения полное приращение функции $z=f(x,y)$ (по определению $Delta z=f(x+Delta x,y+Delta y)-f(x,y)$) равно приращению аппликаты графика функции $z=f(x,y)$ при переходе от точки $M(x,y)$ к точке $M_ (x+Delta x,y+Delta y)$ (рис. 1).
Полный дифференциал заданной функции $z=f(x,y)$ является линейной частью приращения функции и записывается в виде
[dz=f’_ (x,y)cdot Delta x+f’_ (x,y)cdot Delta y.]
Записать полный дифференциал заданной функции
Решение:
Определим частные производные заданной функции:
По определению полного дифференциала некоторой функции найдем:
[dz=1cdot Delta x+2cdot Delta y=Delta x+2cdot Delta y.]
Вычислить полный дифференциал заданной функции $z=xy$ в точке $(1;2)$ при $Delta x=0,1;, , Delta y=0,1$.
Решение:
Определим частные производные заданной функции:
По определению полного дифференциала некоторой функции найдем:
[dz=ycdot Delta x+xcdot Delta y.]
Для функции трех и более переменных, аналогично как для функции двух переменных определяются полный дифференциал:
[dw=f’_ (x,y,z)cdot Delta x+f’_ (x,y,z)cdot Delta y+f’_ (x,y,z)cdot Delta z,] [dw=f’_ (x,y,z. t)cdot Delta x+f’_ (x,y,z. t)cdot Delta y+. +f’_ (x,y,z. t)cdot Delta t.]
Записать полный дифференциал заданной функции
Решение:
Определим частные производные заданной функции:
По определению полного дифференциала некоторой функции найдем:
[dz=zcdot Delta x+zcdot Delta y+(x+y)cdot Delta z.]
Приращения независимых переменных, а именно, $Delta x,, , Delta y,, , Delta z. Delta t$ называют дифференциалами независимых переменных $x,y,z. t$. Обозначение: $dx,dy,dz. dt$.
В новых обозначениях выражения для полного дифференциала принимает следующий вид:
Функция, имеющая непрерывные частные производные в заданной точке, является дифференцируемой в данной точке, при этом полный дифференциал функции в данной точке равен сумме произведений частных производных на дифференциалы независимых переменных соответственно.
Записать полный дифференциал заданной функции
Решение:
Определим частные производные заданной функции:
По определению полного дифференциала некоторой функции найдем:
[dz=zcdot dx+0cdot dy+xcdot dz=zcdot dx+xcdot dz.]
Записать полный дифференциал заданной функции $z=xy$ в точке $(1;2)$.
Решение:
Определим частные производные заданной функции:
По определению полного дифференциала некоторой функции найдем:
[dz=ycdot dx+xcdot dy.]
Запишем полный дифференциал в заданной точке:
[dz|_ =2cdot dx+1cdot dy=2dx+dy.]
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 08 04 2021
🔥 Видео
Полный дифференциалСкачать

Дифференциал функцииСкачать

10. Полное приращение и полный дифференциал функции двух переменныхСкачать

17. Полный дифференциал сложной функции. Инвариантность формы первого дифференциалаСкачать

Дифференциал: частный и полный дифференциалСкачать

11. Полный дифференциал примеры решения (часть 1)Скачать

21. Дифференциал функцииСкачать

✓Дифференцируемая функция. Дифференциал | матан #032 | Борис ТрушинСкачать

24. Дифференциал второго порядка функции двух переменных (часть 1)Скачать

Частные производные функции многих переменныхСкачать

Математика без Ху!ни. Частные производные функции нескольких переменных. Градиент.Скачать

27. Дифференцирование неявной функции двух переменныхСкачать

29. Частные производные и дифференциал функции заданной неявно. примерСкачать

26. Как вычислить дифференциал второго порядка функции двух переменных (часть 3)Скачать

Восстановление функции по полному дифференциалу. Дифференциальное уравнение в полных дифференциалах.Скачать

Дифференциал функцииСкачать

Дифференциал и приращение функцииСкачать

Математический анализ, 32 урок, Частные производные и дифференциалы высших порядковСкачать

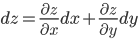
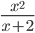 ≡ x^2/(x+2)
≡ x^2/(x+2) 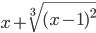 ≡ x+(x-1)^(2/3)
≡ x+(x-1)^(2/3)