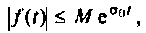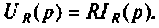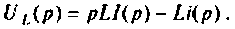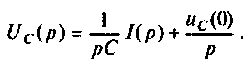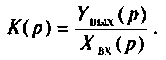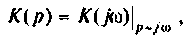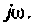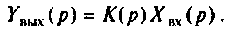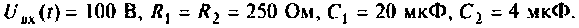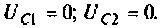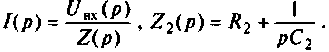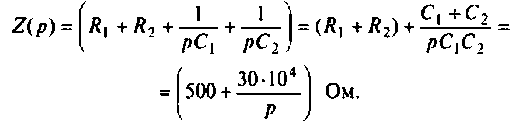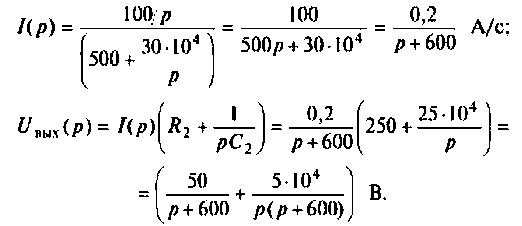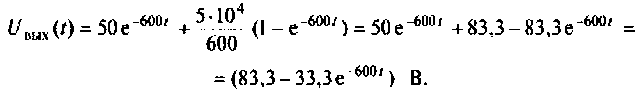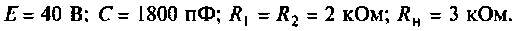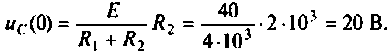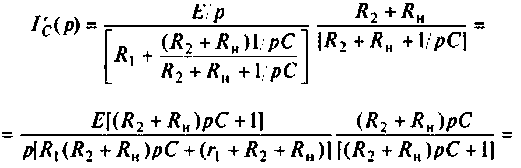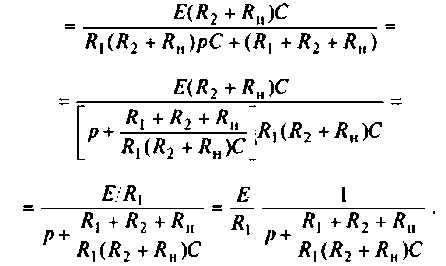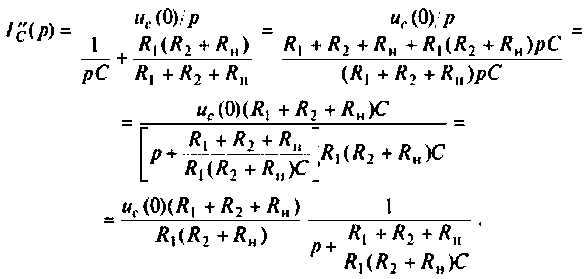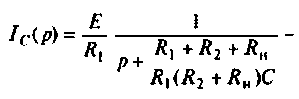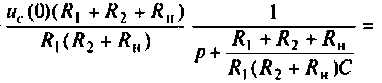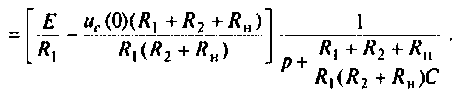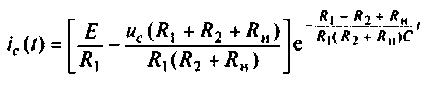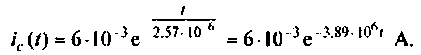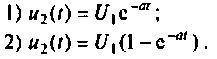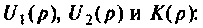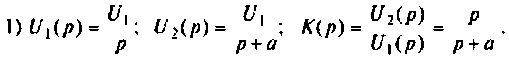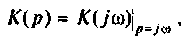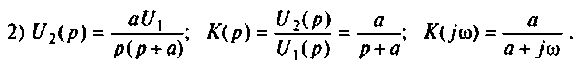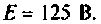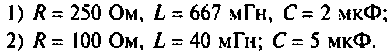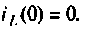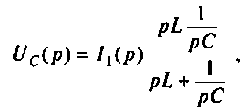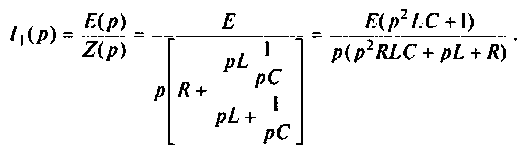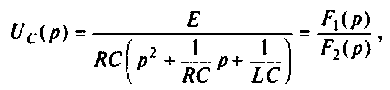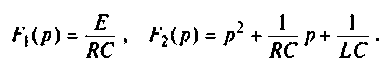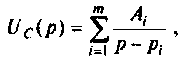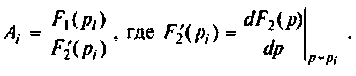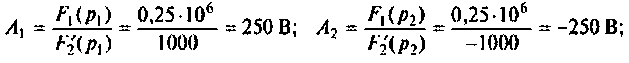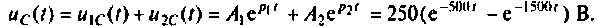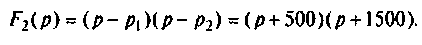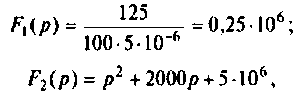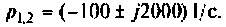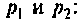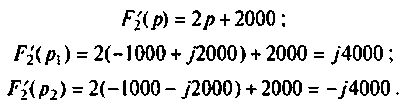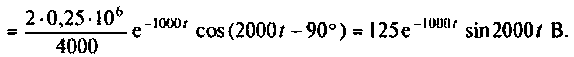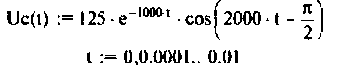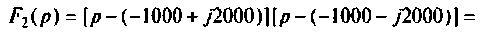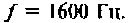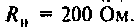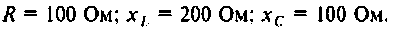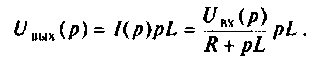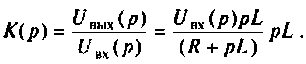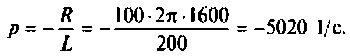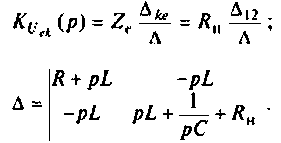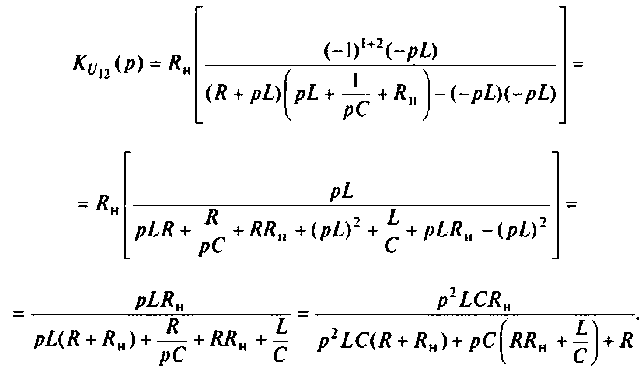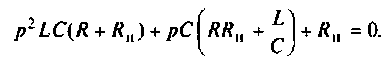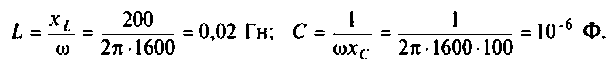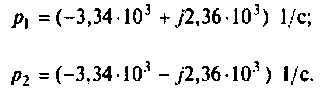Понятие линейного динамического звена
САУ удобно представлять для анализа и при синтезе в виде взаимосвязанной совокупности отдельных элементов динамических звеньев.
Под динамическим звеном понимают в общем случае абстрактное устройство, имеющее вход и выход, и для которого задано уравнение, связывающее сигналы на входе и выходе, как это показано на рис. 1.
Подробное изучение свойств реальных объектов управления и систем автоматического управления приводит к описанию динамических звеньев в виде нелинейных дифференциальных уравнений. Но во многих случаях их можно линеаризовать, то есть заменить нелинейные уравнения линейными, приближенно описывающими процессы в системах. Тем самым осуществляется декомпозиция задач анализа и синтеза систем, то есть первоначально используют линейное представление, а затем осуществляют учет вносимых нелинейностями особенностей. Такому подходу способствует то, что, в большинстве случаев, нормально функционирующая система работает в режиме малых отклонений, при которых нелинейности не проявляются. В дальнейшем мы будем рассматривать преимущественно аппарат изучения линейных систем, а особенности систем других классов: нелинейных, импульсных, цифровых и стохастических, будут излагаться позднее в других учебных дисциплинах.
Если уравнение, связывающее сигналы 

Уравнение линейного динамического звена имеет следующий общий вид:
где 

Использовать такое описание динамического звена в задачах анализа и синтеза систем и объектов управления не рационально, поэтому существуют и иные формы описания и представления динамических звеньев и систем в целом.
Подвергнем уравнение (1) преобразованию Лапласа, считая начальные условия нулевыми и заменяя оригиналы сигналов их изображениями по Лапласу

Используя теоремы преобразования Лапласа линейности и дифференцирования, получим операторное уравнение, связывающие изображения входного и выходного сигналов
Преобразуем уравнение (2) к следующему виду
Получим из (3) отношение изображений выходного и входного сигналов
Отношение (4) не зависит от изображений сигналов, определяется только параметрами самого динамического звена (
Отношение изображений выходного и входного сигналов называют передаточной функцией динамического звена


называют характеристическим уравнением динамического звена, так как знаменатель передаточной функции это характеристический полином дифференциального уравнения, описывающего динамическое звено.
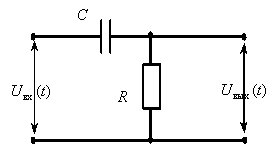
Определим передаточную функцию динамического звена по его принципиальной электрической схеме
По второму закону Кирхгоффа запишем уравнения описывающие схему
С учетом того, что

Получим операторные уравнения
Из второго уравнения выразим значение изображения тока
Подставим полученное выражение в первое уравнение системы

В итоге получаем искомую передаточную функцию

Графически передаточные функции динамического звена представляют в следующем виде:
Если известно изображение входного сигнала и передаточная функция динамического звена, всегда можно найти изображение выходного сигнала при нулевых начальных условиях

В общем случае САУ состоит из множества динамических звеньев, сигналы с выходов звеньев могут суммироваться или вычитаться, суммироваться с внешними для САУ сигналами. Суммирование и вычитание изображений сигналов могут быть представлено графически с помощью суммирующих звеньев:
Показанная выше неоднозначность графического представления вычитания изображений на суммирующем элементе связана с различием в стандартах разных стран.
Используя графическое представление передаточных функций звеньев и суммирующие звенья, можно в графической форме представить операторные уравнения, описывающие САУ. Такое графическое представление операторных уравнений в ТАУ называют структурной схемой.
По математической модели объекта управления в форме системы дифференциальных уравнений определить структурную схему объекта.
Получим систему операторных уравнений, подвергнув исходную систему дифференциальных уравнений преобразованию Лапласа и заменив оригиналы изображениями,
Из первого уравнения системы операторных уравнений, которое описывает динамическое звено объекта управления, после преобразований получим

Тогда передаточная функция этого звена имеет вид

а выражение 

Из второго уравнения системы операторных уравнений, которое описывает динамическое звено объекта управления, после преобразований получим, вводя обозначение,

Тогда передаточная функция этого звена имеет вид

а выражение 

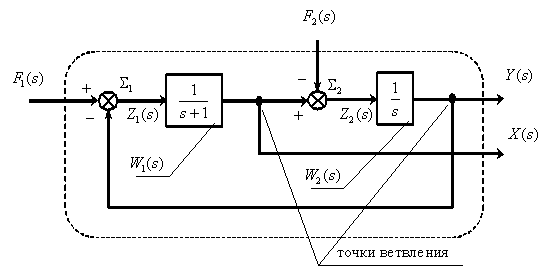
Соединим все фрагменты структурной схемы объекта управления, объединяя одноименные сигналы, либо разветвляя их с помощью точек ветвления , показанных на схеме. В результате получим
Временные характеристики динамического звена
Временной или импульсной характеристикой динамического звена называют реакцию звена на 

Выясним, что представляет собой временная характеристика, то есть почему ее называют характеристикой динамического звена?
Для этого рассмотрим динамическое звено с передаточной функцией
В этом случае, в соответствии с (5), имеем

Получаем, что передаточная функция звена это изображение по Лапласу импульсной характеристики динамического звена. В свою очередь, импульсная характеристика может быть определена по передаточной функции

при использовании разложения в форму Хэвисайта и обратное преобразование Лапласа.
Знание импульсной характеристики позволяет определить реакцию динамического звена на сигнал любой формы.
Для динамического звена с передаточной функцией 

а если легко получить 

Переходной характеристикой или переходной функцией динамического звена называют реакцию динамического звена на 

Для анализа переходной характеристики рассмотрим динамическое звено с передаточной функцией
В этом случае, в соответствии с (5), имеем

По теореме об интегрировании оригинала имеем
Переходная функция является интегралом по времени от импульсной характеристике и наоборот

Переходная характеристика динамического звена может быть определена по передаточной функции
Контрольные вопросы и задачи
Что такое линейное динамическое звено?
Как определить передаточную функцию линейного динамического звена?
Перечислите основные элементы структурных схем систем управления.
Как определить по передаточной функции динамического звена его временные характеристики: импульсную и переходную?
Как по переходной характеристике определить импульсную характеристику динамического звена?
Определите передаточную функцию динамического звена по его принципиальной электрической схеме

Определите передаточную функцию динамического звена по его принципиальной электрической схеме

По математической модели объекта управления в форме системы дифференциальных уравнений определить структурную схему объекта.
- Составление дифференциального уравнения заданной электрической цепи при заданном входном воздействии 10В и следующих исходных данных
- Операторный метод расчета переходных процессов
- Эквивалентные операторные схемы замещения элементов
- Операторные функции электрических цепей
- Анализ переходных процессов в цепях с помощью операторных функций
- Примеры решения задач
- 📸 Видео
Видео:Видеометодичка. Практикум по нахождению передаточных функций по дифференциальным уравнениямСкачать

Составление дифференциального уравнения заданной электрической цепи при заданном входном воздействии 10В и следующих исходных данных
Оглавление.
Составление дифференциального уравнения заданной электрической цепи при заданном входном воздействии 10В и следующих исходных данных. 5
Решение полученного дифференциального уравнения операторным способом, используя преобразования Лапласа. 6
Построение переходного процесса 
Запись выражений и построение частотных характеристик цепи. 9
Получение математического описания цепи в терминах пространства состояний. 13
Получение передаточной функции. 14
Получение дискретной передаточной функции. 14
Список литературы. 16
Введение
В данной работе проводилось исследование электрической цепи с применением математических методов.
В результате различных изменений состояния и параметров, возникают различные переходные процессы, которые являются следствием перераспределения энергии между элементами цепи.
В процессе работы было составлено дифференциальное уравнение, которое описывает входные и выходные параметры цепи, составлено уравнение в терминах пространства состояния, которое послужило проверкой для подтверждения правильности дифференциального уравнения, а также была получена функция в дискретном виде. Все эти виды записи описывают динамический процесс, происходящий в данной схеме электрической цепи.
Найденное дифференциальное уравнение было решено классическим методом и на основе полученного решения, был построен график переходного процесса. Описание в дискретной форме показывает наглядно, насколько различаются графики переходного процесса при разных временах дискретизации.
Для построения графиков использовалась программа MathCAD.
Видео:[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]Скачать
![[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]](https://i.ytimg.com/vi/agDRxLaUWI4/0.jpg)
Операторный метод расчета переходных процессов
Содержание:
Операторный метод расчета переходных процессов:
Для решения линейных дифференциальных и интегродифференциальных уравнений в теории электрических цепей нашел широкое применение так называемый операторный метод, основанный на преобразованиях Лапласа.
Сущность этого метода заключается в том что функции вещественного переменного t преобразуются в функции комплексного переменного
Переход от функции вещественного переменного t к функции комплексного переменного p осуществляется с помощью прямого преобразования Лапласа
Обратный переход от функции комплексного переменного р к функциям вещественного переменного t осуществляется на основании обратного преобразования Лапласа
Функцию 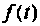
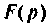
Напомним, что для того чтобы функция 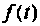
- удовлетворяла условиям Дирихле;
- была равна нулю для отрицательных значений t, т. е. при
- в интервале
не возрастала быстрее, чем некоторая показательная функция
где 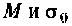
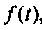
Применение свойств преобразования Лапласа в сочетании с теоремой разложения дает возможность составить таблицы изображений и оригиналов, облетающие и ускоряющие нахождение оригиналов по изображениям [4, 26]. Применение операторного метода совместно с компьютерными математическими программными средами делает анализ и расчет электрических цепей доступным, быстрым и интересным.
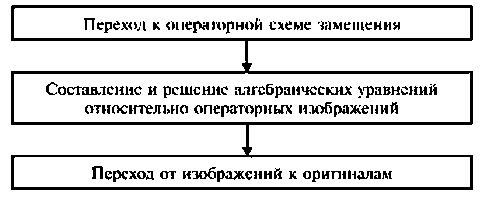
Особенностью метода является необходимость выполнения трех этапов:
Видео:ТАУ│Передаточная функция устройстваСкачать

Эквивалентные операторные схемы замещения элементов
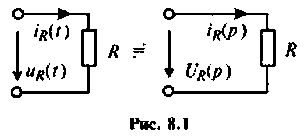
Активное сопротивление:
На рис. 8.1 изображена схема замещения в операторном виде участка цепи с активным сопротивлением. Для этого участка цепи связь между операторным напряжением и током записывается в виде
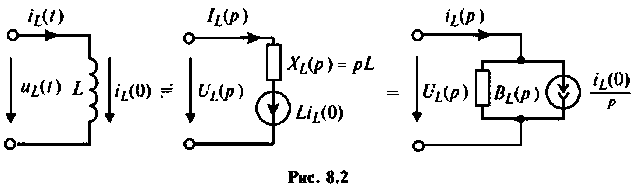
Индуктивность:
Для участка цепи с индуктивностью при ненулевых начальных условиях операторная схема замещения изображена на рис. 8.2.
Связь между операторным напряжением и током записывается в виде
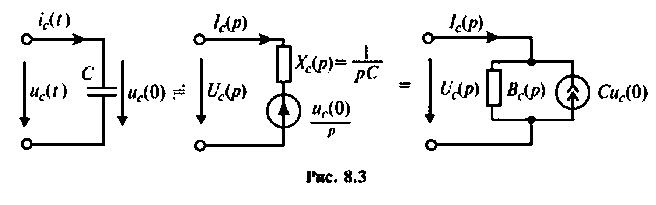
Емкость:
Для участка цепи с емкостью при ненулевых начальных условиях операторная схема замещения изображена на рис. 8.3.
Связь между напряжением и током устанавливает соотношение
В эквивалентных операторных схемах для индуктивности и емкости с ненулевыми начальными условиями возникают дополнительные источники ЭДС 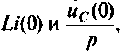
Порядок расчета:
- определяют независимые начальные условия;
- составляют эквивалентную операторную схему замещения для послекоммутационной цепи;
- составляют систему уравнений в операторной форме в соответствии с выбранным рациональным методом расчета эквивалентной схемы замещения и решают ее относительно изображений неизвестных величин;
- для нахождения оригиналов неизвестных величин используют таблицы соответствия, формулы теоремы разложения, компьютерные программные среды и др.
Операторные функции электрических цепей
Основные операторные функции:
Операторной функцией цепи называется отношение изображения по Лапласу выходной величины 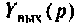
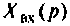
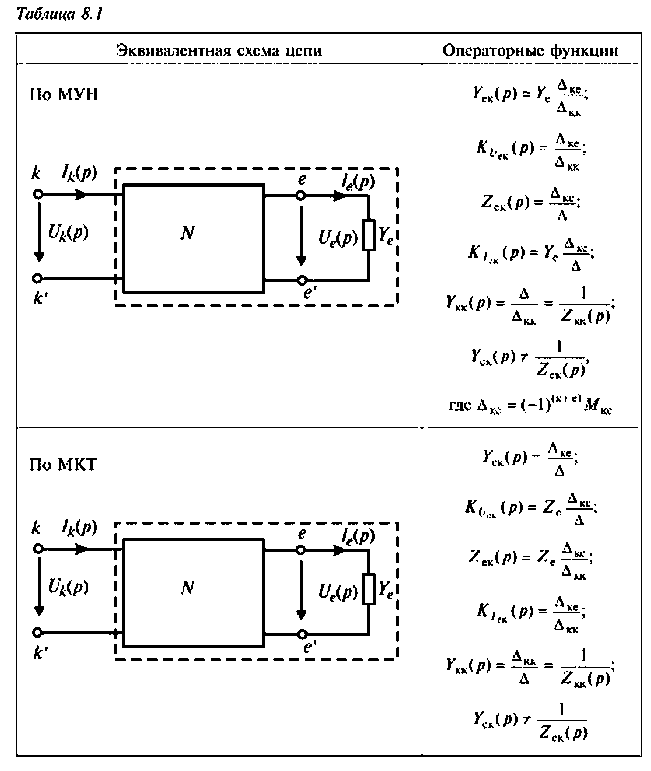
Операторная функция зависит только от параметров цепи и ее схемы. Различают входные и передаточные операторные функции. В табл. 8.1 приведены соотношения для расчета операторных функций сложных цепей.
Для расчета операторных функции можно применять все методы расчета комплексных функций
т. е. комплексная функция является частным случаем операторной при замене оператора 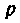
Анализ переходных процессов в цепях с помощью операторных функций
По известной операторной функции цепи и операторному изображению воздействия можно найти реакцию цепи на это воздействие
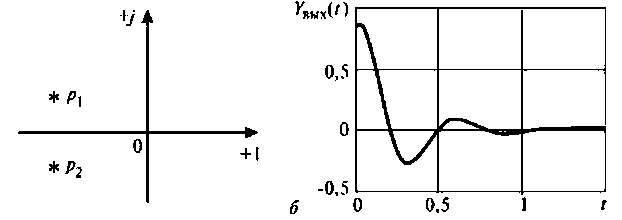
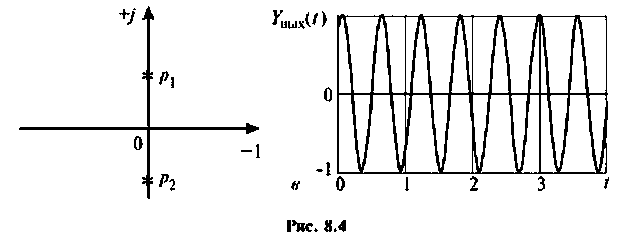
На рис. 8.4 (а—в) приведены временные диаграммы переходных процессов, а также полюсно-нулевое представление на комплексной плоскости.
По расположению полюсов операторной функции можно судить о характере переходное процесса:
- если все полюсы расположены только на отрицательной вещественной полуоси, то переходный процесс в цепи носит апериодический характер;
- если имеются сопряженные полюсы в левой полуплоскости, то переходный процесс носит характер затухающих колебаний;
- если все полюсы расположены только на отрицательной мнимой оси, то переходный процесс в цепи носит характер незатухающих колебаний.
Примеры решения задач
Пример 8.4.1.
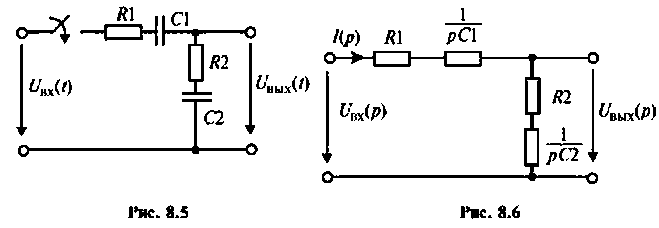
В интегродифференцирующем контуре постоянного тока (рис. 8.5), применяемом для коррекции ЭЦ и САУ. определить напряжение 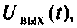
Решение
Определяют независимые начальные условия — напряжения на емкостях. До коммутации ключ был разомкнут, напряжение на емкостях отсутствовало:
Изображают эквивалентную операторную схему замещения после коммутации (рис. 8.6).
Находят изображение напряжения 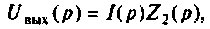
Сопротивление всей цепи определяется выражением
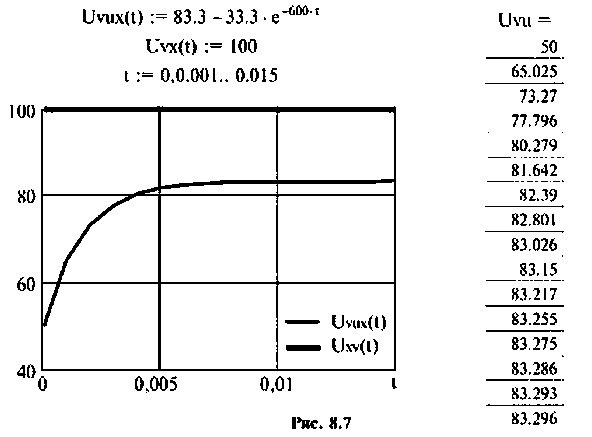
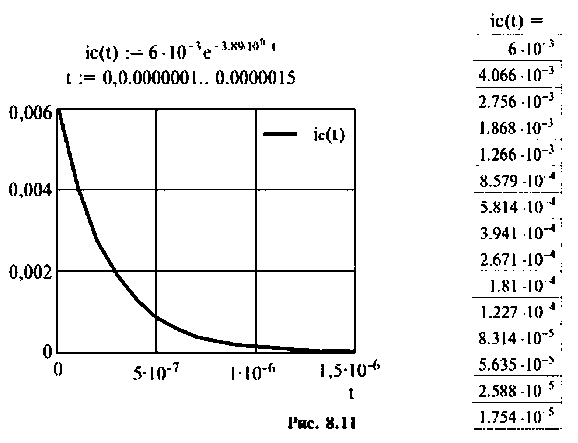
По данному изображению находят оригинал (рис. 8.7) напряжения 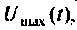
Пример 8.4.2.
К пассивному RС-фильтру нижних частот подключается нагрузка 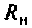
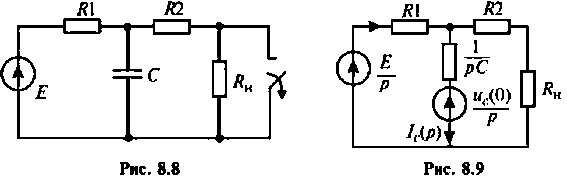
Дано:
Решение
Определяют независимые начальные условия — напряжение на емкости
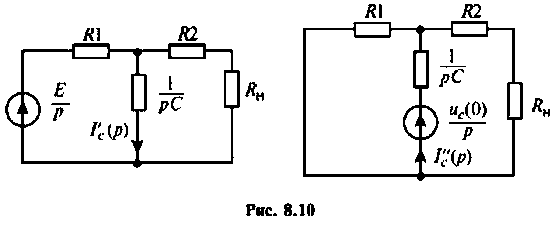
Изображают эквивалентную операторную схему замещения после коммутации (рис. 8.9).
Операторный ток 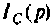
Операторные схемы, соответствующие частичным токам, изображены на рис. 8.10.
Искомый ток
Определяют частичный ток
Аналогично определяют частичный ток
По данному изображению 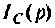
Подставляя числовые значения величин, получают
Строят график тока 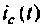
Выводы. До коммутации напряжение на емкости определялось падением напряжения на сопротивлении 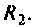
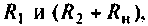
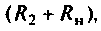
Пример 8.4.3.
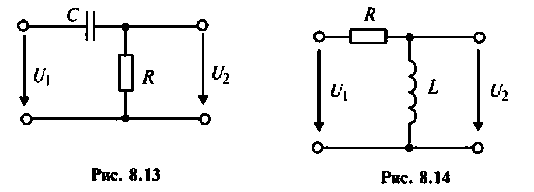
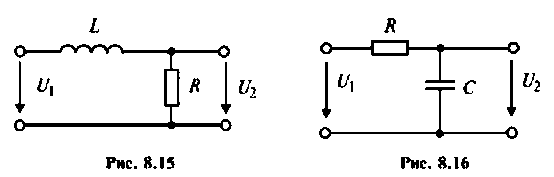
Рассчитать коэффициент передачи по напряжению пассивной цепи (рис. 8.12) и составить ее схему так, чтобы при подключении на вход источника постоянной ЭДС 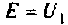
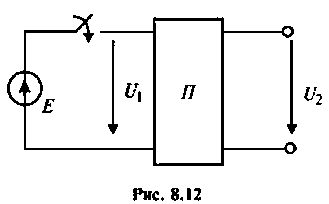
Решение
Применяя преобразования Лапласа, находят изображения
Из прямых преобразований Лапласа и Фурье следует, что
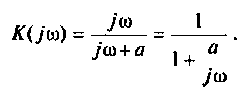
Если принять 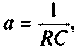
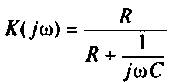
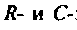
Если принять 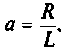
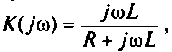
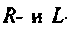
Если принять 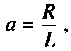
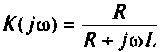
Если принять 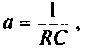
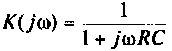
Пример 8.4.4.
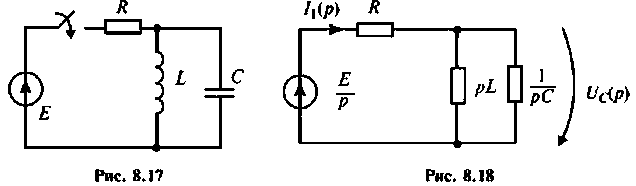
Параллельный колебательный контур (рис. 8.17) включается на постоянное напряжение
Определить напряжение на конденсаторе и построить его опюру, если:
Решение
Определяют независимые начальные условия: напряжение на конденсаторе 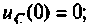
Строят эквивалентную операторную схему замещения после коммутации (рис. 8.18).
Находят изображение напряжения на конденсаторе
По данному изображению находят оригинал по теореме разложения дробно-рациональной функции
где 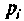
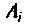
При простых (некратных) полюсах 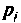
а) Для первого варианта значений:
Полюсы изображения 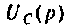
Вычисляют производную 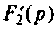
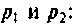
Вычисляют начальные значения компонент
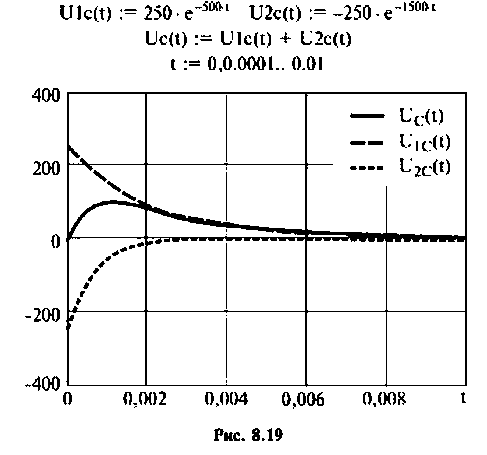
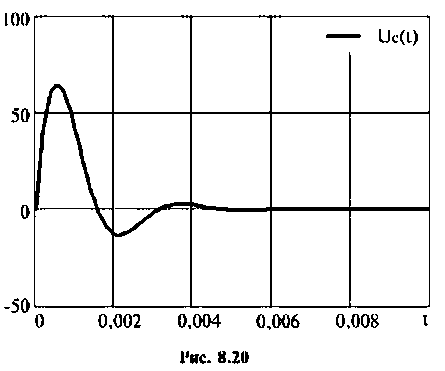
Графики напряжения на конденсаторе и его компонентов получены в среде Mathcad и показаны на рис. 8.19.
Тоn же результат может быть получен по таблице преобразования Лапласа (табл. 8.2, п. 8), если знаменатель изображения напряжения на конденсаторе представить в виде
б) Для второго варианта числовых значений:
а полюсы
Находят производную от 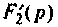
По теореме разложения определяют
где
или
График изменения напряжения 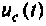
Тот же результат может быть получен по таблице преобразования Лапласа (см. табл. 8.2, п. 13), если знаменатель 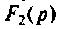
Примечание. Результаты этого примера сравните с результатами примера 6.3. Оцените достоинства и недостатки классического и операторного методов расчета переходных процессов.
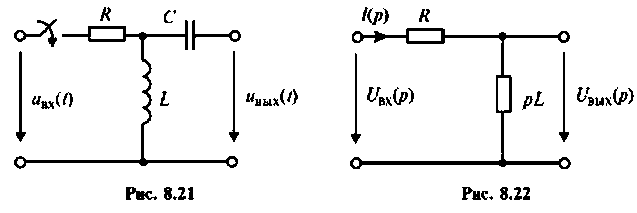
Пример 8.4.5.
После замыкания ключа четырехполюсник (рис. 8.21) используется для работы на частоте
а) коэффициент передачи по напряжению 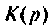
б) характер переходного процесса по кривой переходного процесса.
Дано:
Решение
В режиме холостого хода
Изображают эквивалентную операторную схему замещения. На рис. 8.22 приведена операторная схема замещения при нулевых начальных условиях.
Находят изображение напряжения на выходе
Определяют полюсы операторной функции из уравнения 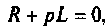
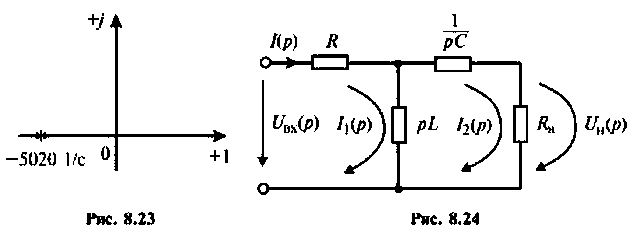
Переходной процесс в цепи имеет апериодический характер, что видно из расположения полюсов на комплексной плоскости (рис, 8.23).
В режиме нагрузки
Изображают эквивалентную операторную схему замещения после коммутации (рис. 8.24).
Определяют операторную функцию 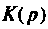
Определяют полюсы операторной функции из уравнения
Для этога вначале вычисляют L и С.
Находят корни уравнения:
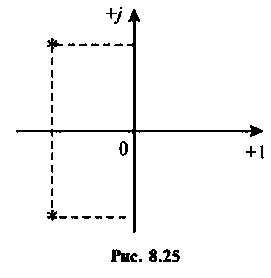
Переходный процесс в цепи имеет характер затухающих колебаний, что видно из расположения полюсов на комплексной плоскости (рис. 8.25).
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Метод пространства состояний электрических цепей
- Синтез электрических цепей
- Цепи с распределенными параметрами
- Электрическая энергия, ее свойства и применение
- Переходные процессы в колебательных контурах
- Расчет переходных процессов
- Классический метод расчета переходных процессов
- Анализ переходных и установившихся процессов методом интеграла свертки
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
📸 Видео
ЗАЧЕМ НУЖНЫ ЭТИ... производные! Математика на QWERTY.Скачать

proТАУ: 1. Передаточная функцияСкачать

ТОЭ - Расчет RC цепи. Найти коэффициент передачи H(jw), построить график АЧХСкачать

7) ТАУ для чайников.Части 3.4 и 3.5 : Передаточная функция. Преобразование Лапласа...Скачать

Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

Линейные цепи и элементы. Дифференциальные уравнения для цепейСкачать

Расчет переходного процесса через ДИФФЕРЕНЦИАЛЬНОЕ уравнение по законам Кирхгофа│Классический методСкачать

Расчет цепи с ИСТОЧНИКОМ ТОКА по законам КирхгофаСкачать

Урок 17. Как работает Интегрирующая и Дифференцирующая RC-цепь | Самое понятное объяснениеСкачать

КАК ТЕЧЁТ ТОК В СХЕМЕ | Читаем Электрические Схемы 1 частьСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Составить дифференциальные уравнения семейств линийСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

13. Как решить дифференциальное уравнение первого порядка?Скачать

7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать





























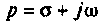
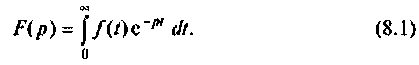
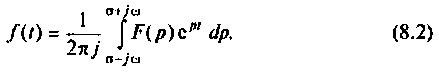
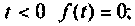
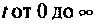 не возрастала быстрее, чем некоторая показательная функция
не возрастала быстрее, чем некоторая показательная функция