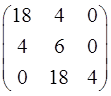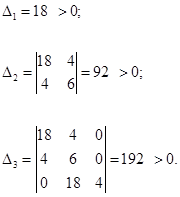1. Найти переходную функцию звена, если передаточная функция имеет вид:
Рисунок 2.1 — Передаточная функция звена
. Найти передаточную функцию и дифференциальное уравнение пассивной электрической цепи относительно u1 (t) и u2 (t).
R=10 Ом, C1=1 мкФ, С2=2 мкФ, L1=1мГн, L2=2 мГн
Рисунок 2.2 — Пассивная электрическая цепь
Преобразуем данную схему
Рисунок 2.3 — Преобразованная пассивная цепь
Значение передаточной функции будет равно:
Дифференциальное уравнение рассматриваемой цепи будет иметь вид:
. Найти передаточную функцию замкнутой САР, у которой задана структурная схема.
Для их нахождения приведем виды соединений звеньев



Интересное из раздела
Исследование узлов и систем автоматического регулирования
Объектом исследования данного курсового проекта является системы автоматического регулирования, их виды, элементарные звенья и их математические модели с те .
Анализ алгоритмов цифровой обработки сигналов. Исследование корректирующих способностей циклических кодов
цифровой сигнал циклический код Цифровой фильтр — в электронике любой фильтр, обрабатывающий цифровой сигнал с целью выделения и/или подавления определённых частот этого .
Моделирование цифро-аналоговых преобразователей
С введением новых телевизионных стандартов, таких как EDTV (телевидение повышенной четкости) и HDTV(телевидение высокой четкости) повышаются требования к АЦП и ЦАП. Некот .
Видео:proТАУ: 1. Передаточная функцияСкачать

Найти передаточную функцию и дифференциальное уравнение пассивной
Название работы: Дифференциальные уравнения и передаточные функции
Предметная область: Коммуникация, связь, радиоэлектроника и цифровые приборы
Описание: Введем понятие звена автоматической системы. При математическом описании системы удобно разбить систему на звенья и для каждого звена записать свое уравнение. Уравнение такого звена связывает две величины: x входная величина или воздействие и y выходная величина или реакция. Пусть момент времени t=0 выбран так что начальные условия на выходе звена являются нулевыми.
Дата добавления: 2015-01-30
Размер файла: 38.88 KB
Работу скачали: 36 чел.
3. Дифференциальные уравнения и передаточные функции.
Введем понятие звена автоматической системы.
При математическом описании системы удобно разбить систему на звенья и для каждого звена записать свое уравнение. Таким образом, звено это часть системы, описываемая одним уравнением. Как одно звено могут быть рассмотрены отдельные элементы системы, совокупности элементов (подсистемы), а также вся система. Также могут использоваться абстрактные звенья, не имеющие прямого соответствия с реальными элементами системы. Для одной системы существует бесконечное множество способов разбиения на звенья (должен быть выбран самый удобный для конкретной задачи).
Структурной схемой называют наглядное изображение математической модели системы. На структурной схеме каждое звено показывается в виде блока, а связи между блоками показываются стрелками.
Рассмотрим линейное звено с одним входом и одним выходом.
Уравнение такого звена связывает две величины: x (входная величина или воздействие ) и y (выходная величина или реакция ). По своему смыслу входная величина является причиной, а выходная следствием.
Линейное звено описывается дифференциальным уравнением вида:
где n и m целые неотрицательные числа, a 0 … a n , b 0 … b m постоянные коэффициенты.
Пусть момент времени t =0 выбран так, что начальные условия на выходе звена являются нулевыми.
y (0)=0, y (1) (0)=0 ,…, y ( n 1) (0)=0.
Выполним преобразование Лапласа от левой и правой частей дифференциального уравнения звена. При этом используем свойство дифференцирования оригинала при нулевых начальных условиях (см. 1.1).
Вместо дифференциального получаем алгебраическое уравнение, где присутствуют уже не функции времени, а изображения входной и выходной величин X ( p ) и Y ( p ). Переменная p это комплексная переменная, заменяющая время в результате преобразования Лапласа.
Дадим следующее определение передаточной функции:
Передаточная функция (ПФ) звена это отношение изображения выходной величины звена к изображению его входной величины при нулевых начальных условиях. Выразим это отношение, обозначив ПФ буквой W .


Передаточная функция является дробно-рациональной функцией переменной p (р это переменная, она не имеет конкретного значения). Смысл ПФ это комплексный коэффициент усиления (передачи) звена при рассмотрении на его входе и выходе изображений величин по Лапласу.
По виду передаточной функции различают идеальные и реальные звенья.
У реальных звеньев порядок числителя передаточной функции не превышает порядка знаменателя: m 
Особенностью идеальных звеньев является то, что эти звенья могут на ограниченные по величине воздействия давать бесконечно большие реакции. Поэтому, идеальное звено нельзя поставить в соответствие с реальным элементом системы. Такие звенья называют также физически нереализуемыми. Реальные элементы систем всегда описываются реальными звеньями.


Передаточную функцию можно преобразовать к следующему виду:

где z 1 , z 2 … z m постоянные числа, называемые нулями передаточной функции, p 1 , p 2 … p n постоянные числа, называемые полюсами передаточной функции, K постоянный множитель. Подстановка p = z i обращает передаточную функцию в ноль. Подстановка p = p i обращает передаточную функцию в бесконечность. Нули и полюсы в общем случае являются комплексными числами.
На структурной схеме передаточную функцию записывают внутри блока, изображающего звено (в символическом или в полном виде). На входе и на выходе звена допустимо показывать как функции времени, так и изображения по Лапласу:
Рассмотрим понятия статического и динамического звена.
Динамическое звено описывается дифференциальным уравнением. Выходная величина динамического звена в каждый момент времени зависит не только от значения входной величины в данный момент времени, но и от ее значений в предыдущие моменты времени.
Статическое звено описывается алгебраическим уравнением (не содержит производных). Выходная величина статического звена в каждый момент времени зависит только от значения входной величины в данный момент времени.
Статическое линейное звено называется пропорциональным звеном и описывается уравнением вида:
где К коэффициент передачи пропорционального звена.
При переходе к изображениям вид уравнения пропорционального звена не изменяется Y ( p )= K · X ( p ). ПФ пропорционального звена W ( p )= K не зависит от переменной p . ПФ динамического звена всегда зависит от переменной р .
Рассмотрим понятие статической характеристики динамического звена.
Статической характеристикой динамического звена называется зависимость выходной величины звена от его входной величины в статическом режиме, т.е. при постоянстве во времени входной и выходной величин.
Условие статического режима:
Для получения уравнения статической характеристики необходимо приравнять к нулю все производные в дифференциальном уравнении звена. В результате можно прийти к алгебраическому уравнению вида
y ст = K ст · x ст ,
где К ст статический коэффициент передачи звена ( K ст = const ).
График статической характеристики линейного звена прямая линия, проходящая через начало координат:
Видео:[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]Скачать
![[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]](https://i.ytimg.com/vi/agDRxLaUWI4/0.jpg)
Контрольная работа: Передаточные функции одноконтурной системы
| Название: Передаточные функции одноконтурной системы Раздел: Рефераты по математике Тип: контрольная работа Добавлен 21:52:15 24 декабря 2010 Похожие работы Просмотров: 508 Комментариев: 14 Оценило: 3 человек Средний балл: 5 Оценка: неизвестно Скачать |





















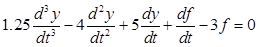 ; б)
; б)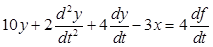 .
.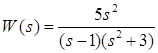 .
.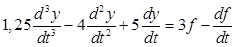 .
. .
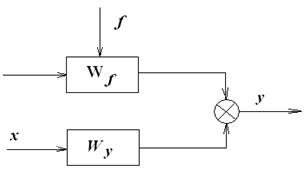
. , то получается уравнение Y(s) = WF(s).F(s). Структурная схема объекта приведена на рис. 1.
, то получается уравнение Y(s) = WF(s).F(s). Структурная схема объекта приведена на рис. 1.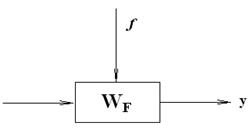
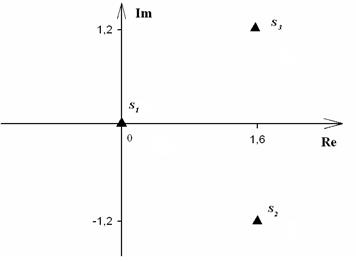
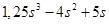 .
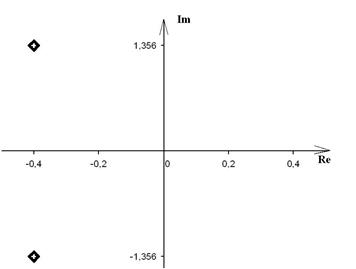
.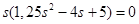 , корни которого:
, корни которого: ,
, 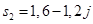 и
и 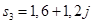 .
.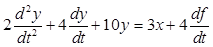 .
.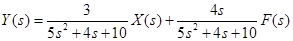 .
.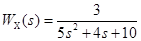 и
и  ,
,
 ,
, .
.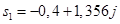 и
и 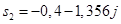 .
.
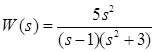
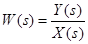 , получим:
, получим: , тогда:
, тогда: .
.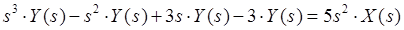
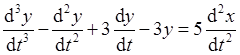 .
.
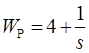 ;
;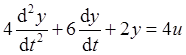 .
.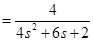 .
.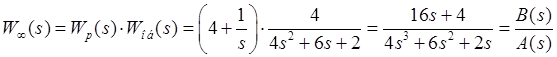
 ;
;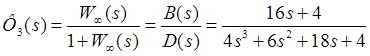 — по заданию;
— по заданию;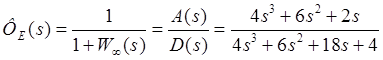 — по ошибке;
— по ошибке;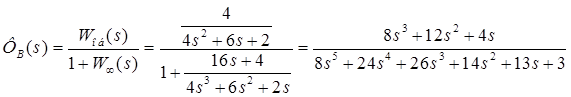 — по возмущению.
— по возмущению.