Найти ортогональный базис подпространства заданного системой уравнений онлайн (6 видео)

Проверить образуют ли вектора базис онлайн калькулятор

Базисом в -мерном пространстве называется упорядоченная система из линейно-независимых векторов.

Введём также некоторые дополнительные понятия, необходимые для дальнейшего изложения.

, где &#x2212 некоторые числа и называется линейной комбинацией векторов .

Если существуют такие числа из которых хотя бы одно не равно нулю (например ) и при этом выполняется равенство:

, то система векторов &#x2212 является линейно-зависимой.

Если же указанное равенство выполняется лишь при условии, что все числа , тогда система векторов &#x2212 является линейно-независимой.

Базис может образовывать только линейно-независимая система векторов. Понятие линейной зависимости/независимости системы векторов, тесно связано с понятием ранга матрицы .

Наш онлайн калькулятор позволяет проверить образует ли система векторов базис. При этом калькулятор выдаёт подробное решение на русском языке.

Содержание

Примеры решений. Линейные пространства
Решения задач: линейные пространства
Базис системы векторов: онлайн-калькулятор
Материалы, которые помогут вам лучше разобраться в теме:
Как найти базис векторов онлайн
📸 Видео

Видео:Как разложить вектор по базису - bezbotvyСкачать

Примеры решений. Линейные пространства

В этом разделе вы найдете бесплатные решения задач о линейных пространствах по темам: проверка линейности подпространства, базис пространства и подпространства, ортогональное подпространство, размерность.

Видео:ОртогональностьСкачать

Решения задач: линейные пространства

Задача 1. Образует ли линейное подпространство пространства $R^4$ множество $V$, заданное по правилу:

Задача 2. Даны векторы $e_1, e_2, e_3, e_4$ и $a$ в стандартном базисе пространства $R^4$.
Требуется:
а) убедиться, что векторы $e_1, e_2, e_3, e_4$ образуют базис пространства $R^4$;
б) найти разложение вектора $a$ по этому базису;
в) найти угол между векторами $e_1$ и $e_2$.

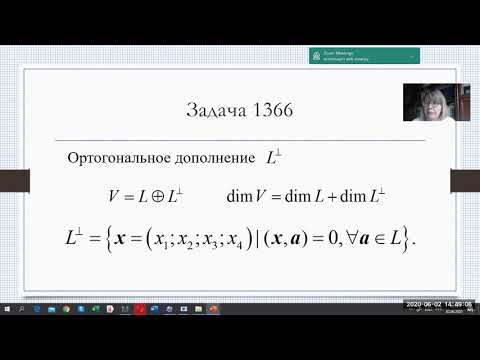
Задача 3.Найти ортогональный базис подпространства $L$, заданного системой уравнений, и базис подпространства $L^$

Задача 4. Для каждого из следующих множеств геометрических векторов определить, будет ли это множество линейным подпространством пространства $V_3$ :
1) радиус-векторы точек данной плоскости;
2) векторы, образующие с данным ненулевым вектором $overline$ угол $alpha$;
3) множество векторов, удовлетворяющих условию $|overline|=1$ .

Задача 5. Пусть $L$ — множество многочленов степени не выше 2, удовлетворяющих условию $p(1)+p'(1)+p»(1)=0$. Доказать, что $L$ — линейное подпространство в пространстве $P_2$. Найти его базис и размерность. Дополнить базис подпространства до базиса всего пространства.

Задача 6. Образуют ли многочлены $p_1(x)=x^3+x^2-1$, $p_2(x)=x^2-2x$, $p_3(x)=x^3+x$, $p_4(x)=x^2-3$ базис в пространстве $P_3$?

Задача 7. Доказать, что матрицы вида $$ begin 2a & a+3b-2c\ b & 5c\ end $$ образуют линейное подпространство в пространстве матриц $M_$. Найти его базис и размерность. Дополнить базис подпространства до базиса всего пространства.

Видео:§48 Ортонормированный базис евклидова пространстваСкачать

Базис системы векторов: онлайн-калькулятор

Векторы, образующие базис, являются линейно независимыми. В противном случае решения нет. Алгоритм в основе калькулятора проверяет соблюдение этого условия. При положительном результате переходит к дальнейшим расчетам.

Доказать, что векторы образуют базис, понадобится при решении задач по аналитической геометрии и выполнении типовых заданий по алгебре. Используйте наш сервис для отработки теорем и правил необходимое количество раз. Вы получите ответ с подробным решением любой задачи бесплатно.

Задайте размерность вектора. Цифра меняется с помощью кнопок «+», «-».
Введите значения базисных векторов в соответствующие окна. Отправьте задание на вычисление кнопкой «Рассчитать».
Способ решения содержит векторное уравнение, которое преобразовывается в матричный вид для решения методом Гаусса. Кнопкой «Показать подробное решение» вы можете развернуть последовательные вычисления.
После вычислений доступен ответ.

Видео:Базис суммы и пересечения линейных пространствСкачать

Материалы, которые помогут вам лучше разобраться в теме:

Видео:Ортогональное дополнение. ПримерСкачать

Как найти базис векторов онлайн

Автоматические расчеты производятся по проверенным формулам и тестируются на примерах. Поэтому с помощью онлайн-калькулятора вы сможете получить точный ответ.

Показать, что векторы образуют базис, несложно. Для этого необходимо:

Найти определитель, построенный на данных векторах. Его значение не должно быть равным нулю.
Произвести дальнейшие вычисления по методу Гаусса.

Раздел онлайн-калькуляторов охватывает не только тему векторов. Здесь собраны все основные типы задач. Сервисом часто пользуются студенты технических специальностей. Также среди нашей аудитории – школьники, их родители, преподаватели, ученые, работники конструкторских бюро и др.

Теперь подготовка к занятиям стала быстрой и доступной. Вы можете сверить ответы и найти у себя ошибку, изучив полученное решение. После нескольких тренировок способ вычислений становится понятным, его можно применять на самостоятельных, семинарах, зачетах.

Мы разработали понятный интерфейс для удобного использования. Если остались вопросы, смотрите инструкцию. Для индивидуального объяснения непонятной темы напишите консультанту и получите скидку на первое занятие с преподавателем.