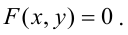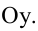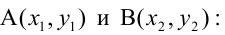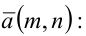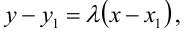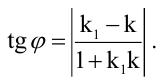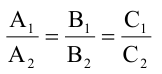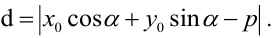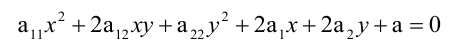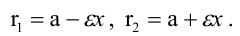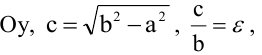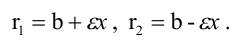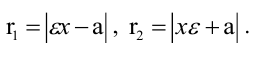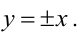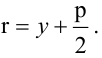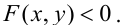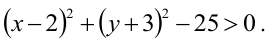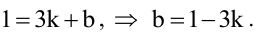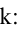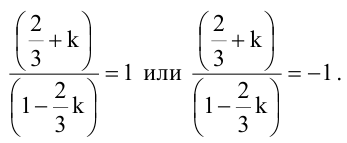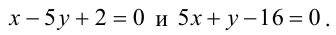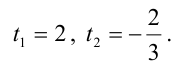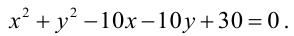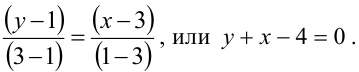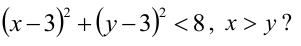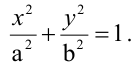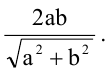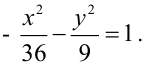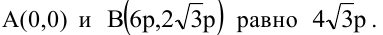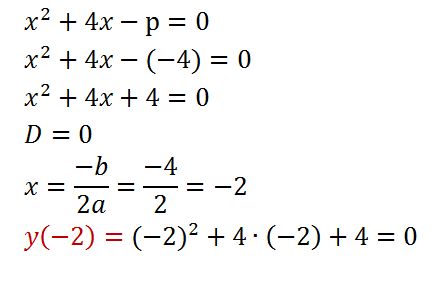Содержание:
- Уравнения прямых и кривых на плоскости
- При каком значении p прямая y=-2x+p имеет с параболой y=x^2+2x ровно одну общую точку
- При каком значении p прямая y=-2x+p имеет с параболой y=x^2+2x ровно одну общую точку
- Итак, координаты точки пересечения графиков: (-2; 0)
- Квадратичная функция. Построение параболы
- Основные понятия
- Построение квадратичной функции
- Алгоритм построения параболы
- Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.
- Уравнение квадратичной функции имеет вид y = a * (x — x₀) 2 + y₀
- Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)
- 📹 Видео
Видео:Задание 22 ОГЭ. Найти точку пересечения прямой и параболы// Построить графики в одной системеСкачать

Уравнения прямых и кривых на плоскости
Уравнения кривых в большом количестве встречаются при чтении экономической литературы. Укажем некоторые из этих кривых.
Кривая безразличия — кривая, показывающая различные комбинации двух продуктов, имеющих одинаковое потребительское значение, или полезность, для потребителя.
Кривая потребительского бюджета — кривая, показывающая различные комбинации количеств двух товаров, которые потребитель может купить при данном уровне его денежного дохода.
Кривая производственных возможностей — кривая, показывающая различные комбинации двух товаров или услуг, которые могут быть произведены в условиях полной занятости и полного объема производства в экономике с постоянными запасами ресурсов и неизменной технологией.
Кривая инвестиционного спроса — кривая, показывающая динамику процентной ставки и объем инвестиций при разных процентных ставках.
Кривая Филлипса — кривая, показывающая существование устойчивой связи между уровнем безработицы и уровнем инфляции.
Кривая Лаффера — кривая, показывающая связь между ставками налогов и налоговыми поступлениями, выявляющая такую налоговую ставку, при которой налоговые поступления достигают максимума.
Уже простое перечисление терминов показывает, как важно для экономистов умение строить графики и анализировать уравнения кривых, каковыми являются прямые линии и кривые второго порядка — окружность, эллипс, гипербола, парабола. Кроме того, при решении большого класса задач требуется выделить на плоскости область, ограниченную какими-либо кривыми, уравнения которых заданы. Чаще всего эти задачи формулируются так: найти наилучший план производства при заданных ресурсах. Задание ресурсов имеет обычно вид неравенств, уравнения которых даны. Поэтому приходится искать наибольшее или наименьшее значения, принимаемые некоторой функцией в области, заданной уравнениями системы неравенств.
В аналитической геометрии линия на плоскости определяется как множество точек, координаты которых удовлетворяют уравнению
Пусть на плоскости задана прямоугольная декартова система координат. Прямая на плоскости может быть задана одним из уравнений:
1. Общее уравнение прямой:
Вектор 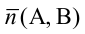
2. Уравнение прямой с угловым коэффициентом:
где 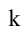
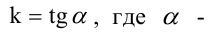
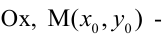
Уравнение (2.2) принимает вид 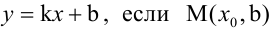
3. Уравнение прямой в отрезках:
где а и b — величины отрезков, отсекаемых прямой на осях координат.
4. Уравнение прямой, проходящей через две данные точки —
5. Уравнение прямой, проходящей через данную точку 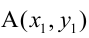
6. Нормальное уравнение прямой:
где 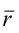
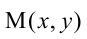
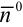
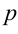
Нормальное уравнение прямой в координатной форме имеет вид:
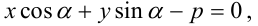
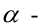
Уравнение пучка прямых с центром в точке 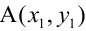
где 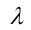
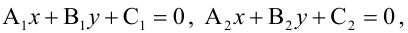
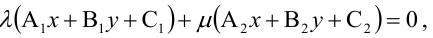
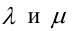
Величина угла между прямыми 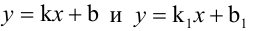
Равенство 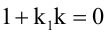
Для того, чтобы два уравнения

Уравнения (2.7), (2.8) задают две различные параллельные прямые, если 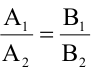
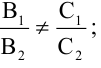
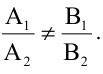
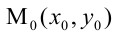
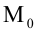
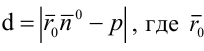
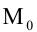
Общее уравнение кривой второго порядка имеет вид:
Предполагается, что среди коэффициентов уравнения 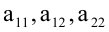
Уравнение окружности с центром в точке 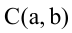

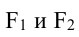
Эллипс, заданный уравнением (2.10), симметричен относительно осей координат.
Параметры а и b называются полуосями эллипса.
Пусть 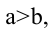
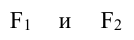
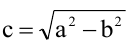
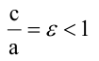
Расстояния от точки 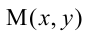
Если же 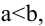
Если а=b, то эллипс является окружностью с центром в начале координат радиуса а.
Гиперболой называется геометрическое место точек, разность расстояний которых от двух данных точек 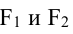
Каноническое уравнение гиперболы:
Гипербола, заданная уравнением (2.11), симметрична относительно осей координат. Она пересекает ось 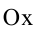
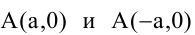
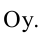
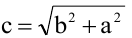
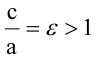
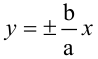
Расстояния от точки 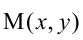
Гипербола, у которой а=b, называется равносторонней, ее уравнение 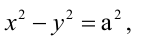
Гиперболы 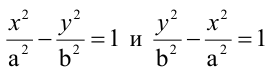
Каноническое уравнение параболы имеет два вида:
1. 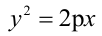
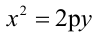
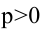
Парабола, уравнение которой 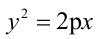
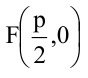
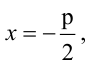
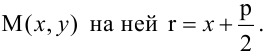
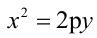
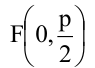
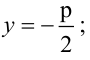
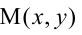
Уравнение 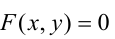
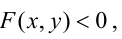
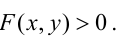
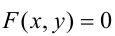
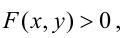
Прямая, уравнение которой 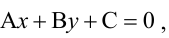
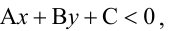
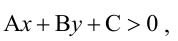
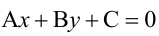
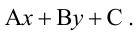
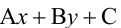
Точно так же решаются и нелинейные неравенства с двумя неизвестными.
Например, решим неравенство 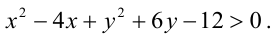
Уравнение 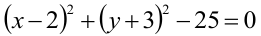
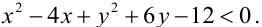
Пример:
Составьте уравнения прямых, проходящих через точку А(3,1) и наклоненных к прямой 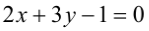
Решение:
Будем искать уравнение прямой в виде 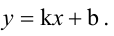
Величина угла между прямыми 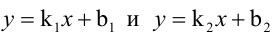
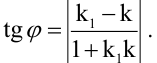
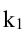
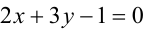
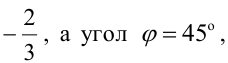
Имеем два значения 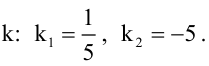
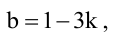
Пример:
При каком значении параметра t прямые, уравнения которых 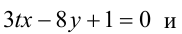
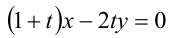
Решение:
Прямые, заданные общими уравнениями, параллельны, если коэффициенты при x и y пропорциональны, т.е. 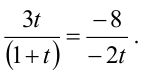
Пример:
Найти уравнение общей хорды двух окружностей: 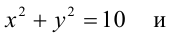
Решение:
Найдем точки пересечения окружностей, для этого решим систему уравнений: 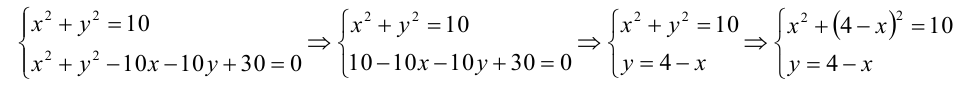
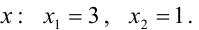
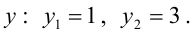
Пример:
Как расположены на плоскости точки, координаты которых удовлетворяют условиям
Решение:
Первое неравенство системы определяет внутренность круга, не включая границу, т.е. окружность с центром в точке (3,3) и радиуса 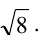
Пример:
Вычислить длину стороны квадрата, вписанного в эллипс, уравнение которого
Решение:
Пусть 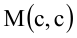
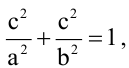
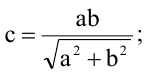
Пример:
Зная уравнение асимптот гиперболы 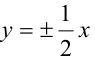
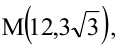
Решение:
Запишем каноническое уравнение гиперболы: 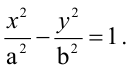
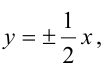
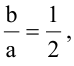
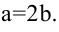
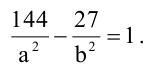
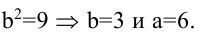
Пример:
Вычислить длину стороны правильного треугольника АВС, вписанного в параболу с параметром р, предполагая, что точка А совпадает с вершиной параболы.
Решение:
Каноническое уравнение параболы с параметром р имеет вид 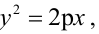
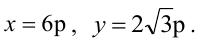
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Плоскость и прямая в пространстве
- Определитель матрицы
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Производные тригонометрических функции
- Производная сложной функции
- Пределы в математике
- Функции многих переменных
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Составляем уравнение прямой по точкамСкачать

При каком значении p прямая y=-2x+p имеет с параболой y=x^2+2x ровно одну общую точку
Видео:Найти абсциссу второй точки пересечения параболы и прямойСкачать

При каком значении p прямая y=-2x+p имеет с параболой y=x^2+2x ровно одну общую точку
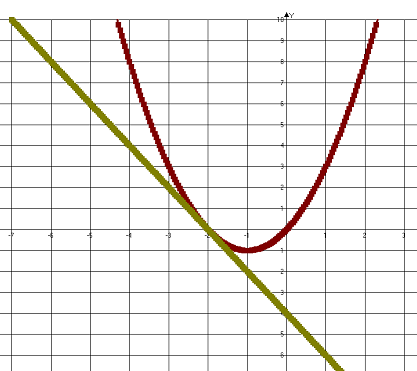
При каком значении p прямая y=-2x+p имеет с параболой y=x^2+2x ровно одну общую точку? Найдите координаты этой точки., Постройте в одной системе координат данную параболу,и прямую при найденном значении p.
- ОДЗ данных функций – вся числовая прямая.
Найдем значение параметра р.
Так как прямая и парабола пересекаются в одной точке, то координаты этой точки будут общими для обеих функций.
Тогда можно приравнять функции.
Получаем уравнение 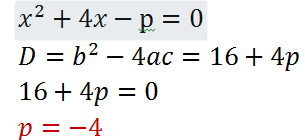
Так как общая точка у графиков одна, то уравнение должно иметь один корень. Следовательно, его дискриминант должен быть нулевым.
Вычислим координаты точки пересечения.
Для этого подставим найденное значение параметра в уравнение
Видео:КАК НАЙТИ ВЕРШИНУ ПАРАБОЛЫСкачать


Итак, координаты точки пересечения графиков: (-2; 0)
Далее будем строить графики функций.
Смотрите видеоурок с подробным решением данной задачи.
Видео:Найти точку пересечения прямой и плоскостиСкачать

Квадратичная функция. Построение параболы
О чем эта статья:
8 класс, 9 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:ОГЭ Задание 23 Парабола Прямая Единственная общая точкаСкачать

Основные понятия
Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ: наглядно.
- Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
График функции — это объединение всех точек, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.
Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.
Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Построение квадратичной функции
Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:
|
График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 :
Точки, обозначенные зелеными кружками называют базовыми точками. Чтобы найти их координаты для функции y = x 2 , нужно составить таблицу:
x
y
Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов.
График функции y = –x 2 выглядит, как перевернутая парабола:
Зафиксируем координаты базовых точек в таблице:
x
y
Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:
- Если старший коэффициент больше нуля a > 0, то ветви параболы напрaвлены вверх.
- Если старший коэффициент меньше нуля a 2 + bx + c, для построения которой нужно решить квадратное уравнение ax 2 + bx + c = 0. В процессе найдем дискриминант D = b 2 — 4ac, который даст нам информацию о количестве корней квадратного уравнения.
Рассмотрим три случая:
- Если D 0,то график выглядит так:
- Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
- Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:
Если a > 0, то график выглядит как-то так:
0″ height=»671″ src=»https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=»602″>
На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:
Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.
Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).
На изображении отмечены основные параметры графика квадратичной функции:
Видео:8 класс. Найти координаты точек пересечения параболы с осями координатСкачать

Алгоритм построения параболы
Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.
Видео:Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.
Разберем общий алгоритм на примере y = 2x 2 + 3x — 5.
Как строим:
- Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
- Найдем дискриминант квадратного трехчлена 2x 2 + 3x — 5.
D = b 2 — 4ac = 9 — 4 * 2 * (-5) = 49 > 0
В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:
2x 2 + 3x — 5 = 0 2 + 3x — 5 = 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAPoAAAAyCAYAAAB1V8bkAAAJyElEQVR4Ae2c16sUwRLGfdRX/wXFB30QFFQUQUyIKCIGBEEQzCCoKIgB01ExZwVz4JpzztljwJxzzjlnrcuvL33unD2zOzO7OzvuThU0u5N6uuvrr7u6unrKiYpqQDVQ8BooV/A11AqqBlQDokTXRqAaiIEGlOgxAFmrqBpQomsbUA3EQANK9BiArFVUDSjRtQ2oBmKgASV6DEDWKqoGlOjaBlQDMdBAQRH9z58/8vv3b5P+/v2bMXy/fv0S8kxMGWesGRgNpIMXz7jhkg28CxmWgiH69+/f5dSpU7JixQpZtmyZXLx4UX7+/JkUOxoGjSaVTJw4UVatWiUbNmwoSYcPH071iF7zqYGgeNlsT58+LZMnTy7BA2y2bNkib9++tbfor4sGCobogD19+nR5/fq1nDx5Upo0aSLHjh2TZD39x48f5ebNmy4q+d8pRo327dtLo0aNTF6NGzeWevXqCeRXyVwDQfHijXTMmzZtMjiAL6lu3brSuXNnuXfvXuaFKuAcCobojOQDBgwwgD948EAg5ubNm42Z54bfjRs3ZMqUKW6XzDk6jP379wsjD/LmzRtZt26dvHr1KukzesG/BoLiRc5gceXKFZM4/vbtmxw6dEguXbokP3788P/yGN5ZMET/8uWLvHv3Tt6/f2/Muh49esj169eTQupF9MQHIfm1a9cST+txmhoIipfba86fPy9Hjx4VrDOV1BooGKJTTYh++fJlGTt2rCxevNgcJ6t+EKIz3587d26yrPR8mhoIglfiK549e2Y6dHBU8dZA3hH9+PHjYhNmnFO+fv1qTOwDBw5Ily5dhF+nQ47ndu/ebdLChQule/fuJcecp9E477d5d+zYUW7fvm0P9TeABixW/AbBCz+LffbChQtl3rh69WpZsmSJjuZlNON+Iu+IDkGZW+N427Ztm6nVp0+f5MiRI6Zh2Dl1hw4dZOjQoaVGdebc1oM+a9Ys48Sxx/y6zfUePnwoVapUcdeenvXUQLp4LV261OA8bdo0g5nzRR8+fJBhw4YJeav400DeEf3Ro0dmZGD+/fLlS1NLzLjhw4fLmDFjhEaA4DHv16+fGeHdVOHXdKczqVy5slsWes6HBtLF6/HjxwZn/CLPnz8v9aZbt25Jt27dlOiltJL6IO+I7lYdTPY1a9bIjBkz5M6dO7Jjxw5hRN++fXtSb6xfos+ZM0cqVark9trQzrEmXFxc7LnOH1oBQs44HbycRTpz5oy0a9funyA6DkGW/NavX19mauIsc+J/OkCmJliRL168ME7FVM7jxOeDHhcE0ak05KD3P3v2rFkWO3HihHz+/DmpPlh3XbRoUdLr9gL5LF++3B6G+nv//n3ZuHGjDBw4UDp16pS0kwq1EDnKPChezmI9efJEtm7dmnJVxXl/WP8PHjxopoxXr141RG3Tpo0JsPLzPqaaLVq0kDp16kjDhg2lb9++JgbEz7Pp3FMwRKfyBLkwX2fpxivqjbm8Nf1TKY77WK/NhVBuGvGoUaNMHID1N+Ti3VG8IwhezvIR5gwm/EYlrBgMGTJE9u3bZxy4YDV69Gjf/py9e/fKypUrjSVKLEDYqwcFRfSoQM/2e2fOnGmivgqd6NnWWy7zI3CqefPmUlRUVOIXgrzly5cXfEZewr2Y/XTuyaI3vfIIcj1tolM4lpyIBZ83b56MGzdO9uzZY0YjwkSfPn0apBx6r0MDYRBd8XIoOAt/sRiZU0N4az2OHz9eKlSo4MvSgOgs6RKIBYdIYUraRMfsYpkL84m5cc+ePY1DYv78+dKnTx/B2eAlmKldu3b1TISy5luII8s/XnWbNGmSMC9PlDCIrniJcXB6YcJ15s9+JHEkrlq1qixYsMDPowLRcRqzSgSHiOkI0xeUNtHpxXBUIQQ3tGrVKnLniC8N58FNYRBd8QoOPES2Php8Agw2dvR25gZRcaaNHDnSeTrlf/JxdhTsuMQacJ5LmUHAi2kT3b6HyrNBoXXr1uYUBXVThr3f+YuCcGp4JZRsFYAV8K8lt1hremqveuE4RAeJEgbR7Tvigpfb1JG6e2HCde5DCJbCM16rVi2T2D9BiLVT6Agwv3GsgSXPumHqfAZ+sLqCNWfbNQ455ve8MwxJm+gsXeF0YFcXPRlRaAiebD/OCO5l/XDQoEGeCTPHhqZWq1ZN/rVElF2iTJ061bNemHkEhiRKGESPG141atRIVKtZevXT3tjz7kcYgIioZDRmtyM6Zk09sf0zbYIndkBgabFt27ZmeZeYAgQzvmLFimWe9VMOP/ekTXTWMXv37m16uF69esmECRNMZdgDzgcgVIJrwLm8Vr9+fSECjM4wG6J4ZUOL/8+DgQdSwwGccIRkk4jITBRGaZZM8V/ZlRRGdIJlwJzBsX///gKPwpK0iY7HkArSgKgwu8XYMnju3LmkgSr0ZNZUCatCfvLFtKIHtj2sn2dycY8NmCGcF6cQIwXx+dmQfMMLfEj/qjA1Yx29ZcuWpRLmfaLcvXtXBg8eLCNGjChxUoM1mBAdt3btWmP9ZatTT3w/x2kTHcKytAB5EeYmyYiDecpWz9mzZyf9EIRb4cI6Rw/KikGcLI98w4vlWkKYC0Uw5xkEMeGt4A/Akc28P+wBMG2i28L6+WV7IruRmjVrVmK6+HkujHuYL+3atcuUhbm/SlkNRI0Xn/iqWbOmaTNlS5d/ZzDzITOhslFJTohO5Rg98WDaOUoUFabXpBExV2JThBI9OQpR4YX1x3SQb/UxOBSCYO2yA48RPCqJFdGZmxN8w/q/Ej11k4uK6ERXMqflw4+FQvTUms7N1VgRnYgndq2RlOipG1gURCf2myhLpldNmzZVoqeGKNDV2BAdj+bOnTuNcpTo3m0k10THrCVohCAiRInujVGQO2JDdJYA8bQTpIJHt3bt2mZtk1FEpawGck10PrRB4BEf4QQjgqIIK2UbqErmGsgJ0fE2AmL16tWFj/oRwpprYcRgVCcR+URsPkELBCyolNZAFHgRVcZyrcWoQYMGwtd97KfBSpdQj4JqICdEZ3kBkwwQIZZXLHDQSvi9H687G/wJgyREkl+7McdvHnG4L0q8WG9mUOCDnASf4DxVyVwDOSF65sXMXg6QnYbMMh+/fjfgZK8EmlMqDYAPzji7WyyqQSFVGfPxWuyIno8gaZlVA5lqQImeqQb1edVAHmhAiZ4HIGkRVQOZakCJnqkGI3m+WIrKlZOi45G8XF+ahxpQouchaKbIx4uU6PmKXQTlVqJHoPTMX/lM/tOuSIozz0hziIkGlOgxAVqrGW8NKNHjjb/WPiYaUKLHBGitZrw1oESPN/5a+5hoQIkeE6C1mvHWwH8BSUfSiO3XWNEAAAAASUVORK5CYII=»>
- Координаты вершины параболы:
- Точка пересечения с осью OY находится: (0; -5) и ей симметричная.
- Нанести эти точки на координатную плоскость и построить график параболы:
2 + 3x — 5 = 0″ height=»671″ src=»https://lh6.googleusercontent.com/TYyA5dFfh0ZKINaPSps3Y_X1mCv8Mhv_8bNG3_dPbZud1AEsvo7UBFmVQNm1GcR1CQFo6HE1lNjYaAgepQUTQiK_ay_Fnuv7LEsB53woHkFO66W0R1PP8QfGsFcYzaR_h4AJdLxC» width=»602″>
Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Уравнение квадратичной функции имеет вид y = a * (x — x₀) 2 + y₀
Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2x 2 + 3x — 5 при а = 1, то второй коэффициент является четным числом.
Рассмотрим пример: y = 2 * (x — 1) 2 + 4.
Как строим:
- Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:
- построить y = x 2 ,
- умножить ординаты всех точек графика на 2,
- сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- сдвинуть его вдоль оси OY на 4 единицы вверх.
- Построить график параболы для каждого случая. 2 + y₀» height=»431″ src=»https://lh5.googleusercontent.com/_zgF-CXWf4Yy0p2OnBYSJkUm0zO-mNetq5feU6LIPEbIgSrO9kdr2ti_tr7Gg3yTMOlJVnuZgG0HleAFfAzG7yr7ELHT6KSMqMrRHkHqt-VcgIiSZx80cVj0zlPMBzEM0wAWQ-L6″ width=»602″>
Видео:Найти координаты пересечения параболы и прямойСкачать

Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)
Рассмотрим следующий пример: y = (x − 2) × (x + 1).
Как строим:
Данный вид уравнения позволяет быстро найти нули функции:
(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.
Определим координаты вершины параболы:
Найти точку пересечения с осью OY:
с = ab = (−2) × (1) = −2 и ей симметричная.
Отметим эти точки на координатной плоскости и соединим плавной прямой.
📹 Видео
Как легко составить уравнение параболы из графикаСкачать

№976. Найдите координаты точки пересечения прямых 4x + 3y-6 = 0 и 2х+у-4 = 0.Скачать

Известно, что парабола проходит через точку В(-1; -1/40, и её вершина находится в начале координатСкачать

10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Графики сложных функций. Подготовка к ОГЭ. Задание № 22. Вебинар | МатематикаСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Пересечение прямой и параболы.Скачать

96 Алгебра 9 класс Пересикаются ли парабола и прямаяСкачать

Как найти вершину параболы?Скачать