- 4xdx 3ydy 3x 2ydy 2xy 2dx
- Ответ или решение 2
- РАЗДЕЛ • Математика
- Лучшие эксперты в этом разделе
- Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)
- Найти общий интеграл дифференциального уравнения 4xdx 3ydy 3x 2 ydy 2xy 2 dx
- Решебник Кузнецова Л. А. V Дифференциальные уравнения
- Задание 1. Найти общий интеграл дифференциального уравнения.
-         Прежде, чем Вы начнёте скачивать свои варианты, попробуйте решить задачу по образцу, приведённому ниже для варианта 10
- Решение.
-         Заданное уравнение является дифференциальным уравнением с разделяющимися переменными. Разделим переменные. Для этого поделим обе части равенства на .         В результате получим
- 📽️ Видео
Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать
4xdx 3ydy 3x 2ydy 2xy 2dx
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать
Ответ или решение 2
4xdx – 3ydy = 3x^2ydy – 3xy^2dx;
(4x + 3xy^2)dx – (3y + 3x^2y)dy = 0;
2x(2 + (3/2)y^2)dx – (1 + x^2)3ydy = 0;
Делим оба члена на (1 + x^2)(2 + (3/2)y^2):
2x / (x^2 + 1)dx – 3y / ((3/2)y^2 + 2)dy = 0;
Интегрируем:
∫2x / (x^2 + 1)dx – ∫3y / ((3/2)y^2 + 2)dy = C;
Каждый из интегралов равен:
∫2x / (x^2 + 1)dx = 2 ∫x / (x^2 + 1) dx = ln (x^2 + 1) + C;
∫3y / ((3/2)y^2 + 2)dy = 3∫ y /( (3/2)y^2 + 2)dy =
= ln ( (3/2)y^2 + 2) + C = ln (3y^2 + 4) + C ;
ln (x^2 + 1) – ln (3y^2 + 4) + C ;
Ответ:ln (x^2 + 1) – ln (3y^2 + 4) + C ;
Версия системы:
7.78 (18.11.2019)
JS-v.1.34 | CSS-v.3.35
Общие новости:
28.04.2019, 09:13
Последний вопрос:
17.11.2019, 18:31
Всего: 150984
Последний ответ:
17.11.2019, 02:39
Всего: 259420
Последняя рассылка:
17.11.2019, 22:45
РАЗДЕЛ • Математика
Консультации и решение задач по алгебре, геометрии, анализу, дискретной математике.
[администратор рассылки: Гордиенко Андрей Владимирович (Профессионал)]
Лучшие эксперты в этом разделе
| Коцюрбенко Алексей Владимирович Статус: Модератор Рейтинг: 1350 | Лысков Игорь Витальевич Статус: Старший модератор Рейтинг: 130 | kovalenina Статус: Практикант Рейтинг: 127 |
| Перейти к консультации №: |
Здравствуйте эксперты! Помогите решить примеры.
Полный дифференциал:
1) (2-9xy^2)xdx+(4y^2-6x^3)ydy=0;
2) e^-y dx-(2y+xe^-y)dy=0;
Интегральный множитель:
1. ydy=(xdy+ydx)*sqrt(1+y^2);
2. (y-1/x)dx+dy/y=0;
Состояние: Консультация закрыта
Здравствуйте, Magma!
Предлагаю решение первого уравнения:
Удачи 
0 
Отправлять сообщения
модераторам могут
только участники портала.
ВОЙТИ НА ПОРТАЛ »
регистрация »
Здравствуйте, Magma!
Решение 2):
(e -y dx-xe -y dy)-2ydy=0
d(xe -y )-d(y 2 )=0
xe -y -y 2 =C
| Консультировал: Орловский Дмитрий (Мастер-Эксперт) Дата отправки: 18.11.2010, 10:34
Отправлять сообщения
Возможность оставлять сообщения в мини-форумах консультаций доступна только после входа в систему. Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать  Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5 Ввод распознает различные синонимы функций, как asin , arsin , arcsin Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x) Список математических функций и констант : • ln(x) — натуральный логарифм • sh(x) — гиперболический синус • ch(x) — гиперболический косинус • th(x) — гиперболический тангенс • cth(x) — гиперболический котангенс • sch(x) — гиперболический секанс • csch(x) — гиперболический косеканс • arsh(x) — обратный гиперболический синус • arch(x) — обратный гиперболический косинус • arth(x) — обратный гиперболический тангенс • arcth(x) — обратный гиперболический котангенс • arsch(x) — обратный гиперболический секанс • arcsch(x) — обратный гиперболический косеканс Видео:Частное решение дифференциального уравнения. 11 класс.Скачать  Найти общий интеграл дифференциального уравнения 4xdx 3ydy 3x 2 ydy 2xy 2 dx
| Видео:Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать  Решебник Кузнецова Л. А. |
. 
.    )
. 
. 
. 
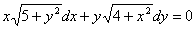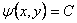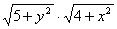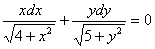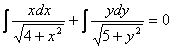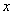    и     
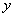    под знак дифференциалов 
. 
. 
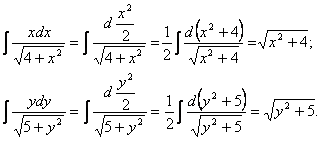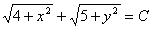