Вычисление объёмов
- Услуги проектирования
- Двойной интеграл
- Вычисление объёмов
Видео:Вычисление объемов тел вращения (применение определенного интеграла)Скачать
Вычисление объёмов
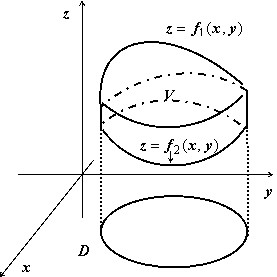
Объём тела, ограниченного сверху и снизу поверхностями $mathbf < textit > =mathbf < textit > _ (mathbf < textit > $,$mathbf < textit > )$, $mathbf < textit > =mathbf < textit > _ (mathbf < textit > $,$mathbf < textit > )$, $(x,y)in D$, с боков — цилиндрической поверхностью с образующими, параллельными оси $mathbf < textit > $, равен $v=iintlimits_D < left[ right]dxdy > $; эта формула очевидно следует из геометрического смысла двойного интеграла.
Основной вопрос, который надо решить — на какую координатную плоскость проектировать тело, чтобы выкладки были наиболее простыми.
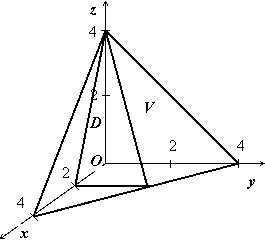
Найти объём тела $V:left[ < begin y=0,;z=0, \ x+y+z=4,; \ 2x+z=4. \ end >right.$
Решение:
Тело изображено на рисунке. Перебором возможностей убеждаемся, что проще всего описать это тело, если отправляться от его проекции на ось $mathbf < textit > $:
$V:left[ < begin (x,z)in D, \ 0leqslant yleqslant 4-x-z. \ end >right.$
Область $mathbf < textit > $ — треугольник, ограниченный прямыми $mathbf < textit > $ = 0, $mathbf < textit > $ = 0, 2$mathbf < textit > +mathbf < textit > $ = 4, поэтому
Найти объём области, ограниченной поверхностями $mathbf < textit > ^ +mathbf < textit > ^ +mathbf < textit > ^ =mathbf < textit > ^ $,
Решение:
Первая поверхность — сфера, вторая — цилиндрическая — с образующими, параллельными оси $mathbf < textit > $ < в уравнении нет $mathbf < textit > $ в явной форме). Построить в плоскости $mathbf < textit > $ кривую шестого порядка, заданную уравнением $(mathbf < textit > ^ +mathbf < textit > ^ )^ =mathbf < textit > ^ (mathbf < textit > ^ +mathbf < textit > ^ )$, в декартовой системе координат невозможно, можно только сказать, что она симметрична относительно осей и точка $mathbf < textit > (0,0)$ принадлежит этой кривой. Пробуем перейти к полярным координатам. $r^6=R^2r^4(cos ^4varphi +sin ^4varphi );r^2=R^2((cos ^2varphi +sin ^2varphi )^2-2cos ^2varphi sin ^2varphi )=R^2(1-frac )=$
$=R^2(1-frac )=R^2frac ;r=Rfrac < sqrt > .$ Эту кривую построить уже можно. $r(varphi )$ максимально, когда $cos 4varphi =1;(varphi =0,frac =frac ,frac =pi ,frac =frac )$, минимально, когда
$cos 4varphi =-1;(varphi =frac ,frac ,frac ,frac ),$ и гладко меняется между этими пределами < точка $mathbf < textit > (0,0)$ не принадлежит этой кривой, где мы её потеряли? > .
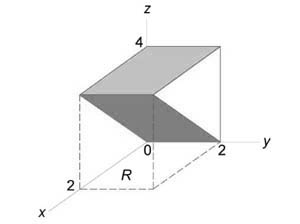
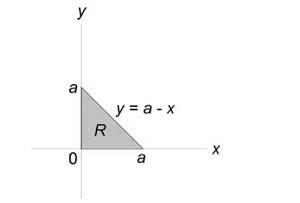
Найти объем тела в первом октанте, ограниченного плоскостями (y = 0,) (z = 0,) (z = x,) (z + x = 4.)
Решение:
Данное тело показано на рисунке.
Из рисунка видно, что основание (R) является квадратом. Для заданных (x, y) значение (z) изменяется от (z = x) до (z = 4 — x.) Тогда объем равен $ < V = iintlimits_R < left[ < left( right) — x >right]dxdy > > = < intlimits_0^2 < left[ < intlimits_0^2 < left( right)dy > >right]dx > > = < intlimits_0^2 < left[ < left. < left( right) >right|_ ^2 >right]dx > > = < intlimits_0^2 < left( right)dx > > = < left. < left( < 8x — 2 >right) >right|_0^2 > = $
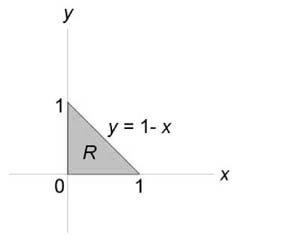
Описать тело, объем которого определяется интегралом (V = intlimits_0^1 intlimits_0^ < left( < + >right)dy > .)
Решение:
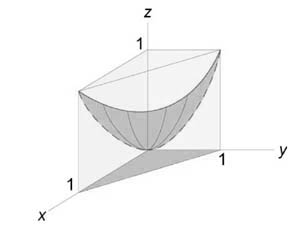
Данное тело расположено над треугольной областью (R,) ограниченной координатными осями (Ox,) (Oy) и прямой (y = 1 — x) ниже параболической поверхности (z = + .) Объем тела равен $ < V = intlimits_0^1 intlimits_0^ < left( < + >right)dy > > = < intlimits_0^1 < left[ < left. < left( < y + frac < < > > >right) >right|_ ^ >right]dx > > = < intlimits_0^1 < left[ < left( right) + frac < < < < left( right) > ^3 > > > >right]dx > > = \ = < intlimits_0^1 < left( < — + frac < < 1 — 3x + 3 — > > >right)dx > > = < intlimits_0^1 < left( < 2 — frac < < 4 > > — x + frac >right)dx > > = < left. < left( < frac < < 2 > > — frac cdot frac < < > > — frac < < > > + frac >right) >right|_0^1 > = < frac — frac — frac + frac = frac . > $
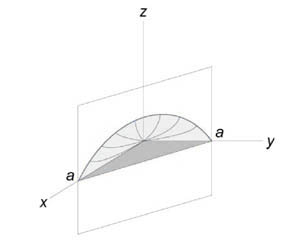
Вычислить объем тела, ограниченного поверхностями (z = xy,) (x + y = a,) (z = 0.)
Решение:
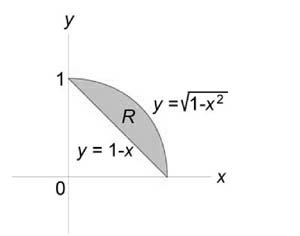
Найти объем тела, ограниченного поверхностями (z = 0,) (x + y = 1,) ( + = 1,) (z = 1 — x.)
Решение:
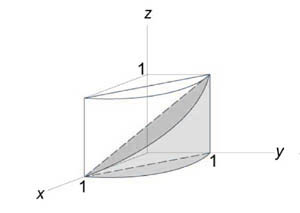
Как видно из рисунков, в области интегрирования (R) при (0 le x le 1) значения (y) изменяются от (1 — x) до (sqrt < 1 — > .)
Вычислим второй интеграл ( = intlimits_0^1 < xsqrt < 1 — > dx > ,) используя замену переменной. Полагаем (1 — = w.) Тогда (-2xdx = dw) или (xdx = largefrac < > normalsize.) Находим, что (w = 1) при (x = 0) и, наоборот, (w = 0) при (x = 1.) Интеграл равен $ < = intlimits_0^1 < xsqrt < 1 — > dx > > = < intlimits_1^0 < sqrt w left( < — frac < > >right) > > = < — frac intlimits_1^0 > = < frac intlimits_0^1 > = < frac intlimits_0^1 < < w^ < largefrac normalsize > > dw > > = < frac left. < left( < frac < < 2 < w^ < largefrac normalsize > > > > >right) >right|_0^1 = frac . > $ Наконец, вычислим третий интеграл. $require < = intlimits_0^1 < left( < 1 — 2x + >right)dx > > = < left. < left( < x — + frac < < > > >right) >right|_0^1 > = < cancel — cancel + frac = frac . > $ Таким образом, объем тела равен $ < V = — — > = < frac — frac — frac = frac — frac approx 0,12. > $
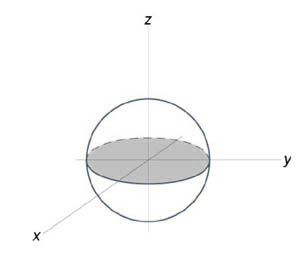
Вычислить объем единичного шара.
Решение:
Уравнение сферы радиусом (1) имеет вид ( + + = 1). В силу симметрии, ограничимся нахождением объема верхнего полушара и затем результат умножим на (2.) Уравнение верхней полусферы записывается как $z = sqrt < 1 — left( < + >right) > .$ Преобразуя это уравнение в полярные координаты, получаем $zleft( right) = sqrt < 1 — > .$ В полярных координатах область интегрирования (R) описывается множеством (R = left[< left( right)|;0 le r le 1,0 le theta le 2pi >right].) Следовательно, объем верхнего полушара выражается формулой $ < < V_ < largefrac normalsize > > = iintlimits_R < sqrt < 1 — > rdrdtheta > > = < intlimits_0^ intlimits_0^1 < sqrt < 1 — > rdr > > = < 2pi intlimits_0^1 < sqrt < 1 — > rdr > . > $ Сделаем замену переменной для оценки последнего интеграла. Пусть (1 — = t.) Тогда (-2rdr = dt) или (rdr = — largefrac <
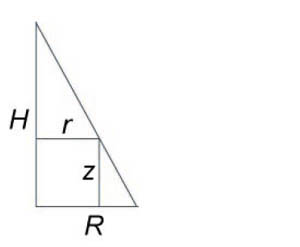
Используя полярные координаты, найти объем конуса высотой (H) и радиусом основания (R).
Решение:
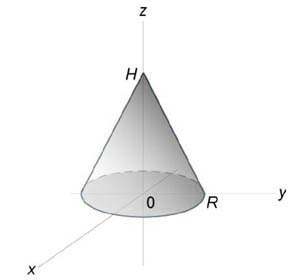
Далее:
Формулы. Равенство функций и эквивалентность формул. Основные эквивалентности
Функции 2-значной логики. Лемма о числе функций. Элементарные функции 1-ой и 2-х переменных
Вычисление объёмов
Теорема об аналоге СДНФ в Pk
Свойства тройного интеграла
Равносильные формулы алгебры высказываний
Дифференциальные характеристики векторного поля
Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам
Критерий полноты . Лемма о несамодвойственной функции
Лемма о построении множества $[F]_$
Булевы функции от $n$ переменных
Вычисление криволинейного интеграла второго рода в случае выполнения условия независимости от формы
Выражение площади плоской области через криволинейный интеграл
Определение двойного интеграла
Соленоидальное векторное поле
Огравление $Rightarrow $
Видео:Объем тела вращения на примере тора. 2 способаСкачать
Объем тела вращения онлайн
Рассмотрим некоторую функцию , непрерывную на отрезке :
Если мы будем вращать данную функцию вокруг оси , то образуется некоторое тело вращения:
Объём полученной фигуры можно посчитать, вычислив вот такой интеграл:
Теперь рассмотрим некоторую функцию , непрерывную на отрезке :
На этот раз будем вращать данную функцию вокруг оси . В результате получим следующее тело вращения:
Его объём вычисляется по формуле:
Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha позволяет вычислить объём тела вращения, заданного практически любой функцией. Для этого, в калькулятор нужно ввести саму функцию, границы в пределах которых будет вычисляться объём тела и выбрать ось вращения.
Видео:Объем через тройной интегралСкачать
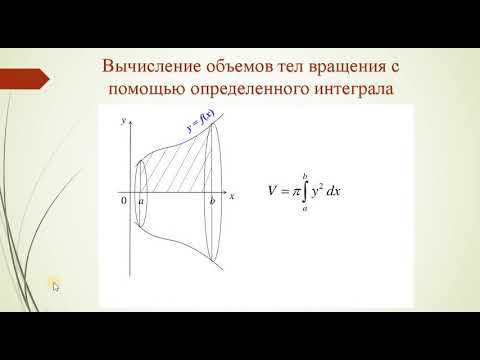
Найти объем тела заданного уравнением
Внимание! Если вы делали заказ после 19.08.2021, вход в новый Личный кабинет — тут
Неправильный логин или пароль.
Укажите электронный адрес и пароль.
Пожалуйста, укажите электронный адрес или номер телефона, который вы использовали при регистрации. Вам будет отправлено письмо со ссылкой на форму изменения пароля или SMS сообщение с новым паролем.
Инструкция по изменению пароля отправлена на почту.
Чтобы зарегистрироваться, укажите ваш email и пароль
Нажимая кнопку «Зарегистрироваться» вы даете согласие на обработку персональных данных в соответствии с политикой конфеденциальности.
📺 Видео
Объем через тройной интеграл в сферической системе координатСкачать
11 класс, 33 урок, Вычисление объемов тел с помощью определённого интегралаСкачать
Интегралы №13 Объем тела вращенияСкачать
Математика без Ху!ни. Определенные интегралы, часть 3. Площадь фигуры.Скачать
Объем через двойной интегралСкачать
Применение определенного интеграла при решении геометр. и физических задач. Практ. часть. 11 класс.Скачать
Вычисление площадей и объемов с помощью определённого интегралаСкачать
Объем параболоида: тройной интеграл в цилиндрической системе координатСкачать
Объем тела вращенияСкачать
Как найти объем. Принцип Кавальери | Ботай со мной #050 | Борис Трушин |Скачать
Математический анализ, 44 урок, Тройной интегралСкачать
Видеоурок "Объем тела вращения"Скачать
Пересечение двух цилиндров: объем и площадь поверхности через двойной интегралСкачать
Математика без Ху!ни. Смешанное произведение векторовСкачать
Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать
Математика без Ху!ни. Уравнение плоскости.Скачать
Урок 28 (осн). Вычисление массы и объема тела по плотностиСкачать
