 Отбор корней в тригонометрических уравнениях
Отбор корней в тригонометрических уравненияхПрактика приемных экзаменов в вузы показывает, что при решении тригонометрических уравнений абитуриенты нередко затрудняются как в выборе способа решения уравнения, так и при отборе его корней.
Проблема отбора корней, отсеивания лишних корней при решении тригонометрических уравнений специфична. Лишние корни могут появиться вследствие того, что в процессе решения произошло расширение области определения уравнения. Запись ответа тригонометрического уравнения часто связана с понятиями объединения и пересечения множеств. Обычно при решении таких уравнений получают серии корней, и в окончательном варианте ответ записывают в виде объединения этих серий. Но как быть, если эти серии пересекаются? Надо ли исключать повторяющиеся корни решения или этого можно не делать?
С понятием пересечения множеств связан и еще один важный вопрос: в ответе не должно быть значений переменной, при которых выражения в левой или правой частях уравнения не определены. Такие значения надо исключить. Для этого надо уметь находить пересечение различных серий.
В предлагаемой работе на конкретных примерах рассматриваются различные способы и приемы при выборе ответа. Надеемся, что данная работа поможет учителям старших классов и самим учащимся при подготовке к вступительным экзаменам в вузы.
1. Отбор чисел на тригонометрическом круге
Проблему отбора корней, отсеивания лишних корней при решении тригонометрических уравнений часто можно решить с помощью изображения чисел на тригонометрическом круге. В ряде случаев этот прием, на наш взгляд, более наглядный и убедительный.
Пример 1. cos x + cos 2x – cos 3x = 1.
2sin x sin 2x – 2sin 2 x = 0,

Из рис. 1 видно, что серия x3(*) включает в себя один из корней серии x1( · ).
Ответ:
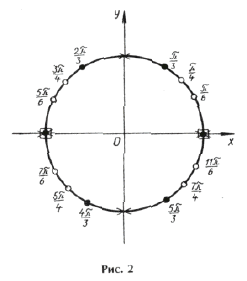
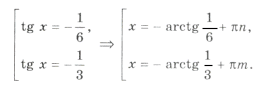
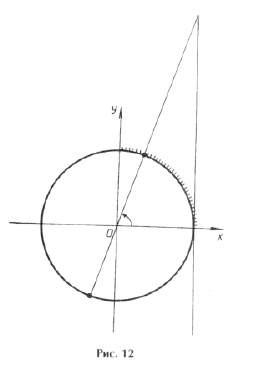
Пример 2. tg x + tg 2x – tg 3x = 0.
Серия x2(*) не удовлетворяет ОДЗ (рис. 2). Серия x1( o ) входит в серию x3( · ), поэтому ответ можно записать одной формулой:
Пример 3.
sin 2x (2cos 2x cos x + cos 7x) = 0,
sin 2x (cos 3x + cos x + cos 7x) = 0,
sin 2x (cos 3x + 2cos 4x cos 3x) = 0,
sin 2x cos 3x (1 + 2cos 4x) = 0,
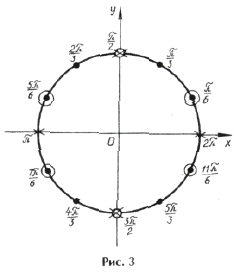
Объединяя все три серии корней, ответ можно записать так:
Пример 4. sin 2 x + sin 2 2x = sin 2 3x.
– (cos 2x + cos 4x) + 1 + cos 6x = 0,
– 2cos 3x cos x + 2cos2 3x = 0,
cos 3x (cos 3x – cos x) = 0,
cos 3x sin 2x sin x = 0,
Серия корней x2 содержится в серии x1 и x3, в чем легко убедиться, изобразив их различными точками на круге, поэтому
ответ:
Пример 5. sin x + sin 7x – cos 5x + cos (3x – 2 p ) = 0.
2sin 4x cos 3x + 2sin 4x sin x = 0,
sin 4x (cos 3x + sin x) = 0,
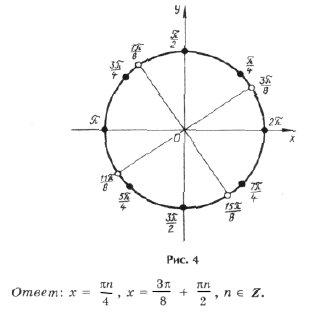
Серия x2 содержится в серии корней x1, а на круге (рис. 4) изобразим точками серии x1( · ) и x3(О), которые не совпадают.
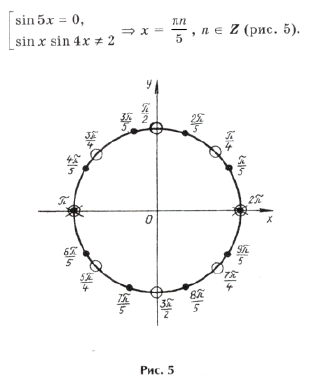
Пример 6. ctg 2x + 2ctg x – tg 2x = sin 5x.
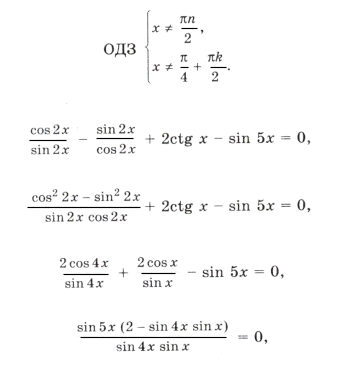
Учитывая ОДЗ, получим
Пример 7.
Иногда случается, что часть серии входит в ответ, а часть нет.
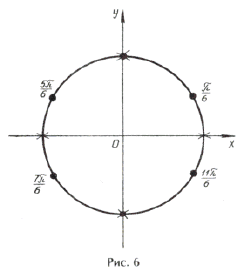
Нанесем на тригонометрический круг (рис. 6) все числа серии 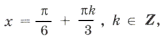
и выбросим корни, удовлетворяющие условию
Оставшиеся решения из серии x1 можно объединить в формулу
2. Отбор корней в тригонометрическом уравнении алгебраическим способом
Изображение корней на тригонометрическом круге не всегда удобно, когда период меньше 2 p .
Пример 8. sin 2 2x + sin 2 3x + sin 2 4x + sin 2 5x = 2.
cos 4x + cos 6x + cos 8x + cos 10x = 0,
2cos 5x cos x + 2cos 9x cos x = 0,
cos x cos 2x cos 7x = 0.
«Период» серий равен p. Рассмотрим те корни из серий x1, x2, x3, которые попадают в промежуток [0; p ]. Это будут:
Сразу видно, что серия x1 содержится в серии x3, а серии x2 и x3 не пересекаются. Значит, ответ можно записать в виде .
Способ алгебраический. Общим знаменателем в сериях x1 и x2 будет 4:
Если x1 = x2, то 2 + 4k = 1 + 2l, но слева – четное число, а справа – нечетное. Равенство невозможно, серии x1 и x2 не пересекаются. Аналогично получаем, что серии х3 и х2 тоже не пересекаются, а вот для серий x1 и x3 получаются формулы
Из равенства 7 + 14k = 1 + 2m получаем m = 7k + 3. Это означает, что для всякого k найдется целое m такое, что будет выполняться равенство 7 + 14k = 1 + 2m, т. е. всякий корень из серии x1 встретится и в серии x3, поэтому серия x1 содержится в серии x3, и в ответе писать ее не надо.
При решении некоторых тригонометрических уравнений их заменяют эквивалентной системой уравнений, а затем находят пересечение множеств решений. Эти пересечения часто найти легко. Но иногда для нахождения решений необходимо решать диафантово уравнение (ax + by = c).
Пример 9.
В данном случае сделать отбор решений на тригонометрическом круге неудобно, так как периоды серий разные. Найдем такие целые k, при которых x = p + 2 p k имеет посторонние корни, удовлетворяющие условию x № 3 p n, n О Z. Пусть p + 2 p k = 3 p n; 1 + 2k = 3n. Отсюда n = 2m + 1 Ю k = 3m + 1. Итак, посторонние корни в серии x = p + 2 p k будет при k = 3m + 1, m О Z.
Пример 10. cos 7x (sin 5x – 1) = 0.
Пересекаются ли эти серии? Из равенства
следует 5k = 14n + 1. Выразим ту неизвестную, коэффициент при которой меньше по абсолютной величине:
– целое число.
Ответ можно записать в виде
.
Пример 11.
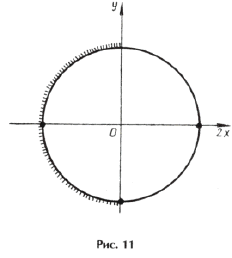
Поскольку наибольшее значение функции y = cos t равно 1, уравнение равносильно системе
Решением уравнения является пересечение серий x1 и x2, т. е. нам надо решить уравнение
Из него получаем уравнение, имеющее решение k = 8t, n = 3t.
Пример 12.
Решением уравнения является пересечение серий x1 и x2;
,
где
– целое число;
Пример 13.
sin 2x sin 4x = 2sin x sin 3x cos x,
sin 2x sin 4x = sin 2x sin 3x,
sin 2x (sin 4x – sin 3x) = 0,
Остается проверить, лежат ли они в области x О R,
Серию x1 проверить легко: поскольку
,
а при n, кратных 8, n = 8l (l О Z), получается как раз x № 2 p l, вся серия x1 исключается. Сложнее обстоит дело с серией x2. Здесь надо выяснить, при каких целых k найдется такое n, что выполняется равенство
,
и исключить такие k. Последнее уравнение приводится к виду 8k + 4 = 7n, причем решать это уравнение надо в целых числах. Из него следует, что n = 4l, поскольку левая часть уравнения делится на 4. Подставляя n = 4l в уравнение, получаем 8k + 4 = 28l, откуда 2k + 1 = 7l. Далее, l должно быть нечетно, l = 2t + 1; поэтому 2k + 1 = 14t + 7, k = 7t + 3. Вот решение и получилось:
Ответ:
3. Отбор корней в тригонометрическом уравнении с некоторыми условиями
Изложенные выше способы отбора корней в тригонометрических уравнениях не всегда применяются в чистом виде: выбор способа зависит от конкретных условий, но иногда эти способы комбинируются.
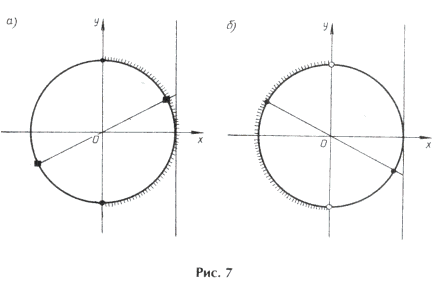
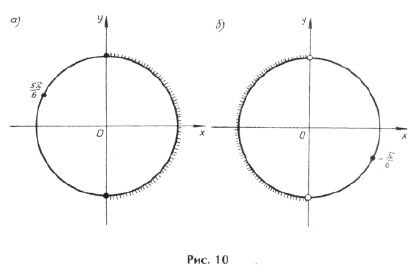
Пример 14. Найти корни уравнения sin 2x = cos x | cos x |,
удовлетворяющие условию x О [0; 2 p ].
Условию cos x і 0 удовлетворяют
из серии
из серии
Наконец,
Пример 15. Найти все решения уравнения
удовлетворяющие условию
так как
то
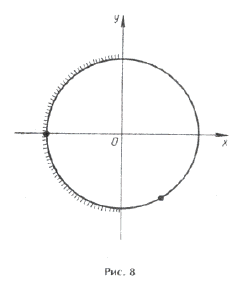
Пример 16. Найти все решения уравнения
принадлежащие отрезку
.
Отметим ОДЗ на тригонометрическом круге (рис. 9):
Отрезку
принадлежит только один промежуток из ОДЗ, а именно
.
Решим уравнение и выберем корни, принадлежащие этому промежутку:
1 + sin 2x = 2cos 2 3x Ю sin 2x = cos 6x,
Из серии
при n = 2 имеем
Из серии
при n = 5 имеем
Пример 17.
Ответ:
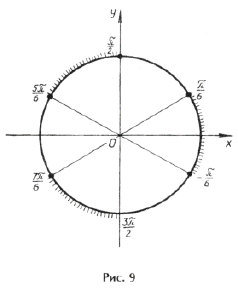
Пример 18. Найти все корни уравнения
которые удовлетворяют условию
.
10sin 2 x = – cos 2x + 3 Ю 10sin 2 x = 2sin 2 x – 1 + 3,
Выберем корни, удовлетворяющие условию задачи. Из серии
При
при
.
Аналогично выберем корни, удовлетворяющие условию задачи, из второй серии. Это будут
.
Пример 19.
sin x и cos x должны быть одинакового знака, а, учитывая первое неравенство, только при sin x > 0 и cos x > 0 система совместна. Значит, x оканчивается в первой четверти. Имеем
1 + 2sin x cos x = 4sin x cos x Ю sin 2x = 1,
Ответ:
Пример 20.
Ответ:
Пример 21.
а)
Но ctg x 0. Решений нет.
б)
Ответ:
.
Примеры для самостоятельного решения
7. Найти все решения уравнения, принадлежащие указанным промежуткам:

Л. Максименко,
Р. Зинченко,
г. АнгарскСодержание
- Основные методы решения тригонометрических уравнений
- п.1. Разложение на множители
- п.2. Приведение к квадратному уравнению
- п.3. Приведению к однородному уравнению
- п.4. Введение вспомогательного угла
- п.5. Преобразование суммы тригонометрических функций в произведение
- п.6. Преобразование произведения тригонометрических функций в сумму
- п.7. Понижение степени
- п.8. Замена переменных
- п.9. Использование ограничений области значений функций
- п.10. Примеры
- 💡 Видео
Видео:Симметрия корней и оптимизация ответов в тригонометрии: часть 1Скачать
Основные методы решения тригонометрических уравнений
п.1. Разложение на множители
Алгоритм простого разложения на множители
Шаг 1. Представить уравнение в виде произведения (f_1(x)cdot f_2(x)cdot . cdot f_n(x)=0) где (f_i(x)) — некоторые функции (тригонометрические и не только) от (x).
Шаг 2. Решить совокупность уравнений: ( left[ begin f_1(x)=0\ f_2(x)=0\ . \ f_n(x)=0\ end right. )
Шаг 3. Найти объединение полученных решений. Записать ответ.Например:
Решим уравнение (2cosx cos2x=cosx) begin 2cosx cos2x-cosx=0\ cosx(2cos2x-1)=0\ left[ begin cosx=0\ 2cos2x-1=0 end right. Rightarrow left[ begin x=fracpi2+pi k\ cos2x=frac12 end right. Rightarrow left[ begin x=fracpi2+pi k\ 2x=pmfracpi3+2pi k end right. Rightarrow left[ begin x=fracpi2+pi k\ x=pmfracpi6+pi k end right. end
Мы видим, что полученные семейства образуют множество из 6 базовых точек на числовой окружности через каждые (60^=fracpi3)
Поэтому: begin left[ begin x=fracpi2+pi k\ x=pmfracpi6+pi k end right. Leftrightarrow x=fracpi6+frac endВозможно, у вас не сразу получится объединять решения, которые частично пересекаются или дополняют друг друга.
Тогда записывайте ответ в виде полученных семейств.
В рассмотренном примере, это пара (fracpi2+pi k, pmfracpi6+pi k), равнозначная c (fracpi6+frac).
Вот только научиться работать с числовой окружностью нужно обязательно, т.к. чем сложнее пример или задача, тем больше вероятность, что этот навык пригодится.Алгоритм разложения на множители со знаменателем
Шаг 1. Представить уравнение в виде произведения $$ frac=0 $$ где (f_i(x), g_i(x)) — некоторые функции (тригонометрические и не только) от (x).
Шаг 2. Решить смешанную систему уравнений: ( begin left[ begin f_1(x)=0\ f_2(x)=0\ . \ f_n(x)=0\ end right.\ g_1(x)ne 0\ g_2(x)ne 0\ . \ g_m(x)ne 0\ end )
Шаг 3. Найти объединение полученных решений для числителя. Исключить все решения, полученные для знаменателя. Записать ответ.Например:
Решим уравнение (ctgx-tgx=frac)
Левая часть уравнения: $$ ctgx-tgx=frac-frac=frac=frac $$ Подставляем, переносим правую часть влево: $$ frac-frac=0 $$ Выносим общий множитель, умножаем на (1/2) слева и справа, получаем: $$ frac=0 $$ В этом уравнении учтено ОДЗ для (ctgx) и (tgx). Поэтому отдельно его не записываем.
Полученное уравнение равносильно системе: begin begin left[ begin cosx-sinx=0\ cosx+sinx=1 end right.\ sin2xne 0 end end Решаем первое уравнение как однородное 1-й степени (см. этот параграф ниже): begin cosx-sinx=0 |: cosx\ 1-tgx=0Rightarrow tgx=1Rightarrow x=fracpi4+pi k end Решаем второе уравнение введением вспомогательного угла (см. этот параграф ниже): begin cosx-sinx=1 | times frac<sqrt>\ frac<sqrt>cosx+frac<sqrt>sinx=frac<sqrt>\ cosleft(fracpi4right)cosx+sinleft(fracpi4right)sinx=frac<sqrt>\ cosleft(fracpi4-xright)=cosleft(x-fracpi4right)=cosleft(x-fracpi4right)=frac<sqrt> Rightarrow x-fracpi4=pmfracpi4+2pi kRightarrow left[ begin x=2pi k\ x=fracpi2+2pi k end right. end Решаем исключающее уравнение для знаменателя: $$ sin2xne 0Rightarrow 2xne pi kRightarrow xnefrac $$
Записываем полученную систему, отмечаем базовые решения на числовой окружности, исключаем нули знаменателя. Получаем: begin begin left[ begin x=fracpi4+pi k\ x=2pi k\ x=fracpi2+2pi kLeftrightarrow x=fracpi4+pi k end right.\ xnefrac end end За счет требования (xnefrac) исключаются семейства (x=fracpi2+2pi k) и (x=2pi k).
Остается только (x=fracpi4+pi k).
Ответ: (fracpi4+pi k)п.2. Приведение к квадратному уравнению
Шаг 1. С помощью базовых тригонометрических отношений и других преобразований представить уравнение в виде $$ af^2(x)+bf(x)+c=0 $$ где (f(x)) — тригонометрическая функция.
Шаг 2. Сделать замену переменных: (t=f(x)). Решить полученное квадратное уравнение: begin at^2+bt+c=0\ D=b^2-4ac, t_=frac<-bpmsqrt> end Шаг 3. Если (f(x)) — синус или косинус, проверить условие (-1leq t_leq 1). Отбросить лишние корни.
Шаг 4. Вернуться к исходной переменной и решить совокупность простейших тригонометрических уравнений ( left[ begin f(x)=t_1\ f(x)=t_2 end right. ) или одно оставшееся уравнение.
Шаг 5. Найти объединение полученных решений. Записать ответ.Например:
Решим уравнение (3sin^2x+10cosx-6=0)
Заменим (sin^2x=1-cos^2x). Получаем: begin 3(1-cos^2x)+10cosx-6=0\ -3cos^2x+10cosx-3=0\ 3cos^2x-10cosx+3=0\ text t=cosx, -1leq tleq 1\ 3t^2-10t+3=0\ D=(-10)^2-4cdot 3cdot 3=64\ t=frac= left[ begin frac13\ 3gt 1 — text end right. end Решаем (cosx=frac13Rightarrow x=pm arccosfrac13+2pi k)
Ответ: (pm arccosfrac13+2pi k)п.3. Приведению к однородному уравнению
Алгоритм решения однородного тригонометрического уравнения 1-й степени
Например:
Решим уравнение (sinx+cosx=0)
Делим на (cosx). Получаем: (tgx+1=0Rightarrow tgx=-1Rightarrow x=-fracpi4+pi k)
Ответ: (-fracpi4+pi k)Алгоритм решения однородного тригонометрического уравнения 2-й степени
Шаг 1. Разделить левую и правую части уравнения на (cos^2x) begin frac=frac\ Atg^2x+Btgx+C=0 end Шаг 2. Сделать замену переменных: (t=tgx). Решить полученное квадратное уравнение: begin at^2+bt+c=0\ D=b^2-4ac, t_=frac<-bpmsqrt> end Шаг 3. Решить совокупность простейших тригонометрических уравнений ( left[ begin tgx=t_1\ tgx=t_2 end right. )
Шаг 4. Найти объединение полученных решений. Записать ответ.Например:
Решим уравнение (6sin^2x-sinxcosx-cos^2x=3)
Приведем уравнение к однородному (чтобы избавиться от тройки справа, умножим её на тригонометрическую единицу): begin 6sin^2x-sinxcosx-cos^2x=3(sin^2x+cos^2x)\ 3sin^2x-sinxcosx-4cos^2x=0 |: cos^2x\ 3tg^2x-tgx-4=0\ text t=tgx\ 3t^2-t-4=0\ D=(-1)^2-4cdot 3cdot(-4)=49\ t=frac= left[ begin -1\ frac43 end right. end Решаем совокупность: ( left[ begin tgx=-1\ tgx=frac43 end right. Rightarrow left[ begin x=-fracpi4+pi k\ x=arctgfrac43+pi k end right. )
Ответ: (-fracpi4+pi k, arctgfrac43+pi k)Обобщим понятие однородного тригонометрического уравнения на любую натуральную степень:
Алгоритм решения однородного тригонометрического уравнения n-й степени
Шаг 1. Разделить левую и правую части уравнения на (cos^n x)
Шаг 2. Сделать замену переменных: (t=tgx). Решить полученное алгебраическое уравнение: begin a_0t^n+a_1t^+. +a_n=0 end Найти корни (t_1, t_2. t_k, kleq n)
Шаг 3. Решить совокупность простейших тригонометрических уравнений ( left[ begin tgx=t_1\ tgx=t_2\ . \ tgx=t_k end right. )
Шаг 4. Найти объединение полученных решений. Записать ответ.Например:
Решим уравнение (2sin^3x=cosx)
Умножим правую часть на тригонометрическую единицу и получим однородное уравнение 3-й степени: begin 2sin^3x=cosx(sin^2x+cos^2x)\ 2sin^3x-sin^2xcosx-cos^3x=0 |: cos^3x\ 2tg^x-tg^2x-1=0\ end Замена (t=tgx) дает кубическое уравнение: (2t^3-t^2-1=0)
Раскладываем на множители: begin 2t^3-t^2-1=t^3-t^2+t^3-1=t^2(t-1)+(t-1)(t^2+t+1)=\ =(t-1)(2t^2+t+1) end Вторая скобка на множители не раскладывается, т.к. (D=1-4cdot 2=-7 lt 0).
Получаем: (2t^3-t^2-1=0Leftrightarrow t-1=0)
Возвращаемся к исходной переменной:
(tgx=1Rightarrow x=fracpi4+pi k)
Ответ: (fracpi4+pi k)п.4. Введение вспомогательного угла
Например:
Решим уравнение (sqrtsin3x-cos3x=1)
Делим уравнение на ( p=sqrt=2: ) begin sqrtsin3x-cos3x=1 |: 2\ frac<sqrt>sin3x-frac12cos3x=frac12\ sinleft(fracpi3right)sin3x-cosleft(fracpi3right)cos3x=frac12\ cosleft(fracpi3right)cos3x-sinleft(fracpi3right)sin3x=-frac12\ cosleft(3x+fracpi3right)=-frac12Rightarrow 3x+fracpi3=pmfrac+2pi kRightarrow 3x= left[ begin -pi+2pi k\ fracpi3+2pi k end right. Rightarrow x= left[ begin -fracpi3+frac\ fracpi9+frac end right. end
Ответ: (-fracpi3+frac, fracpi9+frac)п.5. Преобразование суммы тригонометрических функций в произведение
При решении уравнений вида begin Asinax+Bsinbx+. +Ccoscx+Dcosdx+. =0 end используются формулы, выведенные в §17 данного справочника.
Затем проводится разложение на множители, и находится решение (см. начало этого параграфа).Например:
Решим уравнение (cos3x+sin2x-sin4x=0)
Заметим, что: $$ sin2x-sin4x=2sinfraccosfrac=2sin(-x)cos3x=-2sinxcos3x $$ Подставляем: begin cos3x-2sinxcos3x=0\ cos3x(1-2sinx)=0\ left[ begin cos3x=0\ 1-2sinx=0 end right. Rightarrow left[ begin 3x=fracpi2+pi k\ sinx=frac12 end right. Rightarrow left[ begin x=fracpi6+frac\ x=(-1)^kfracpi6+pi k= left[ begin x=fracpi6+2pi k\ frac+2pi k end right. end right. end Чтобы было понятней, распишем полученные множества в градусах: begin left[ begin x=fracpi6+frac=30^+60^k\ x=fracpi6+2pi k=30^+360^kLeftrightarrow x=30^+60^k=fracpi6+frac\ x=frac+2pi k=150^+360^k end right. end
Получаем, что семейства решений (fracpi6+2pi k) и (frac+2pi k) уже содержатся во множестве (fracpi6+frac). п.6. Преобразование произведения тригонометрических функций в сумму
При решении уравнений вида begin sinaxcdot cosbx=sincxcdot cosdx, sinaxcdot sinbx=sincxcdot cosdx text end используются формулы, выведенные в §18 данного справочника.
Например:
Решим уравнение (sin5xcos3x=sin6xcos2x)
Заметим, что: begin sin5xcos3x=frac=frac\ sin6xcos2x=frac=frac end Подставляем: begin frac=frac |times 2\ sin8x-sin2x=sin8x-sin4x\ sin4x-sin2x=0\ 2sin2xcos2x-sin2x=0\ sin2x(2cos2x-1)=0\ left[ begin sin2x=0\ 2cos2x-1=0 end right. Rightarrow left[ begin 2x=pi k\ cos2x=frac12 end right. Rightarrow left[ begin x=frac\ 2x=pmfracpi3+2pi k end right. Rightarrow left[ begin x=frac\ x=pmfracpi6+pi k end right. end
Семейства решений не пересекаются. Примечание: учитывая ответ предыдущего примера, это же множество решений можно записать в виде: ( left[ begin x=frac\ x=pmfracpi6+pi k end right. Leftrightarrow left[ begin x=fracpi6+frac\ x=pi k end right. )
п.7. Понижение степени
При решении уравнений вида begin sin^2ax+sin^2bx+. +cos^2cx+cos^2dx+. =A end используются формулы понижения степени: begin sin^2x=frac, cos^2x=frac end (см. формулы половинного аргумента, §15 данного справочника).
Например:
Решим уравнение (sin^2x+sin^22x=1)
Расписываем квадраты синусов через формулу понижения степени: begin frac+frac=1\ cos2x+cos4x=0\ 2cosfraccosfrac=0\ cos3xcosx=0\ left[ begin cos3x=0\ cosx=0 end right. Rightarrow left[ begin 3x=fracpi2+pi k\ x=fracpi2+pi k end right. Rightarrow left[ begin x=fracpi6+frac\ x=fracpi2+pi k end right. end
(x=fracpi2+pi k) является подмножеством (x=fracpi6+frac)
Поэтому begin left[ begin x=fracpi6+frac\ x=fracpi2+pi k end right. Leftrightarrow x=fracpi6+frac endп.8. Замена переменных
При решении уравнений вида (f(sinxpm cosx, sinxcosx)=0) используется замена begin t=cosxpm sinx end
Например:
Решим уравнение (sinx+cosx=1+sinxcosx)
Замена: (t=sinx+cosx)
Тогда (t^2=sin^2x+2sinxcosx+cos^2x=1+2sinxcosxRightarrow sinxcosx=frac)
Подставляем: begin t=1+fracRightarrow 2(t-1)=t^2-1Rightarrow t^2-2t+1=0Rightarrow (t-1)^2=0Rightarrow t=1\ sinx+cosx=1 | times frac<sqrt>\ frac<sqrt>sinx+frac<sqrt>cosx=frac<sqrt>\ sinfracpi4 sinx+cosfracpi4 cosx=frac<sqrt>\ cosleft(x-fracpi4right)=frac<sqrt>Rightarrow x-fracpi4=pmfracpi4 + 2pi kRightarrow Rightarrow left[ begin x=2pi k\ x=fracpi2+2pi k end right. end Ответ: (2pi k, fracpi2+2pi k)п.9. Использование ограничений области значений функций
Уравнения вида begin underbrace_<m text> end может иметь решение только, если каждое из слагаемых равно 1.
Поэтому решаем систему: ( begin sinax=1\ sinbx=1\ . \ cosdx=1\ . end )
Находим пересечение (!) полученных семейств решений и записываем ответ.Аналогично, уравнение вида begin underbrace_<m text> end может иметь решение только, если каждое из слагаемых равно -1.
Например:
Решим уравнение (sinx+cos4x=2)
Для этого нужно решить систему: begin begin sinx=1\ cos4x=1 end Rightarrow begin x=fracpi2+2pi k\ 4x=2pi k end Rightarrow begin x=fracpi2+2pi k\ x=frac end end
Пересечением двух семейств решений будет только (fracpi2+2pi k).
Поэтому begin begin x=fracpi2+2pi k\ x=frac end Leftrightarrow x=fracpi2+2pi k endп.10. Примеры
Пример 1. Используя различные методы, решите уравнения:
a) (4sinleft(fracpi2right)+5sin^2x=4)
Приводим уравнение к квадратному:
(5sin^x+4cosx-4=0)
(5(1-cos^2x)+4cosx-4=0)
(-5cos^2x+4cosx+1=0)
(5cos^2x-4cosx-1=0)
Замена: (t=cosx, -1leq tleq 1) begin 5t^2-4t-1=0Rightarrow (5t+1)(t-1)=0Rightarrow left[ begin t_1=-frac15\ t_2=1 end right. end Оба корня подходят. Возвращаемся к исходной переменной: begin left[ begin cosx=-frac15\ cosx=1 end right. Rightarrow left[ begin x=pm arccosleft(-frac15right)+2pi k\ x=2pi k end right. end Ответ: (pm arccosleft(-frac15right)+2pi k, 2pi k)б) (6sinxcosx=5cos2x)
(6sinxcosx=3cdot 2sinxcosx=3sin2x)
Приводим уравнение к однородному 1-й степени:
(3sin2x=5cos2x | : cos2x)
(3tg2x=5Rightarrow tg2x=frac53Rightarrow 2x=arctgfrac53+pi kRightarrow x=frac12 arctgfrac53+frac)
Ответ: (frac12 arctgfrac53+frac)в) (9cos^2x-5sin2x=-sin^2x)
(5sin2x=5cdot 2sinxcosx=10sinxcosx)
Приводим уравнение к однородному 2-й степени:
(sin^2x-10sinxcosx+9cos^2x=0 |: cos^2x)
(tg^2x-10tgx+9=0)
Замена: (t=tgx) begin t^2-10+9=0Rightarrow (t-1)(t-9)=0Rightarrow left[ begin t_1=1\ t_2=9 end right. end Оба корня подходят. Возвращаемся к исходной переменной: begin left[ begin tgx=1\ tgx=9 end right. Rightarrow left[ begin x=fracpi4+pi k\ x=arctg9+pi k end right. end Ответ: (fracpi4+pi k, arctg9+pi k)г) (cos3x-1=cos6x)
Косинус двойного угла: (cos6x=2cos^2 3x-1)
Подставляем и раскладываем на множители:
(cos3x-1=2cos^2 3x-1)
(cos3x-2cos^2 3x=0)
(cos3x(1-2cos3x)=0) begin left[ begin cos3x=0\ 1-2cos3x=0 end right. Rightarrow left[ begin 3x=fracpi2+pi k\ cos3x=frac12 end right. Rightarrow left[ begin x=fracpi6+frac\ 3x=pmfracpi3+2pi k end right. Rightarrow left[ begin x=fracpi6+frac\ x=pmfracpi9+frac end right. end Чтобы проверить пересечения, распишем семейства решений через градусы: begin left[ begin x=fracpi6+frac=30^+60^k=<. -90^,-30^,30^,90^,150^. >\ x=pmfracpi9+frac= left[ begin -20^+120^k=<. -140^,-20^,100^. >\ 20^+120^k=<. -100^,20^,140^. > end right. end right. end Семейства не пересекаются.
Ответ: (fracpi6+frac, pmfracpi9+frac)д) (sqrtsin2x-cos2x=-sqrt)
Разделим на (p=sqrt) и введем дополнительный угол:
(frac<sqrt>sin2x-frac12 cos2x=-frac<sqrt>)
(frac12cos2x-frac<sqrt>sin2x=frac<sqrt>)
(cosleft(2x-fracpi3right)=frac<sqrt>)
(2x-fracpi3=pmfracpi6+2pi k)
(2x=fracpi3pmfracpi6+2pi k= left[ begin -frac+2pi k\ fracpi2+2pi k end right. )
( left[ begin x=-frac+pi k\ x=fracpi4+pi k end right. ) Семейства решений не пересекаются.
Ответ: (-frac+pi k, fracpi4+pi k)е) (cos^2x+cos^2 2x=cos^2 3x+cos^2 4x)
Формула понижения степени: (cos^2x=frac)
Подставляем: begin frac+frac=frac+frac\ cos2x+cos4x=cos6x+cos8x\ 2cosfraccosfrac=2cosfraccosfrac |: 2\ cos3xcosx=cos7xcosx=0\ cos3xcosx-cos7xcosx=0\ cosx(cos3x-cos7x)=0\ cosxleft(-2sinfracsinfracright)=0\ -2cosxsin5xsin(-2x)=0\ 2cosxsin5xsin2x=0\ cosxsin5xsin2x=0\ left[ begin cosx=0\ sin5x=0\ sin2x=0 end right. Rightarrow left[ begin x=fracpi2+pi k\ 5x=pi k\ 2x=pi k end right. Rightarrow left[ begin x=fracpi2+pi k\ x=frac\ x=frac end right. end Семейство решений (x=fracpi2+pi k) (базовые точки 90°, 270° на числовой окружности) является подмножеством для (x=frac) (базовые точки 0°, 90°, 180°, 270°). Поэтому: begin left[ begin x=fracpi2+pi k\ x=frac\ x=frac end right. Rightarrow left[ begin x=frac\ x=frac end right. end Ответ: (frac, frac)Пример 2*. Решите уравнения:
a) begin frac-frac+frac=0 end ОДЗ: (tgxne pm 3)
1) Если (cosxne 0), то последнее слагаемое (frac=frac<frac><frac>=frac)
Получаем: begin frac-frac+frac=0\ frac=0\ frac=0\ end Замена: (t=tgx) begin fracRightarrow begin t^2+7t-30=0\ tnepm3 end Rightarrow begin (t+10)(t-3)=0\ tnepm3 end Rightarrow begin left[ begin t=-10\ t=3 end right.\ tnepm3 end Rightarrow\ t=-10 end Получаем: begin tgx=-10\ x=arctg(-10)+pi k=-arctg10+pi k end
2) Проверим, является ли (cosx=0) решением.
При (cosx=0, x=fracpi2+pi k, tgxrightarrowinfty). Первое слагаемое (fracrightarrowfracrightarrow 0)
Второе слагаемое (fracrightarrowfracrightarrow 0)
Третье слагаемое (fracrightarrowfrac=1ne 0)
Сумма слагаемых в пределе (tgxrightarrowinfty) равна (0+0+1=1ne 0)
(cosx=0) решением не является.
Ответ: (-arctg10+pi k)б) (frac+1=7frac)
ОДЗ: (cosxne 0, xnefracpi2+pi k) begin |cosx|= begin cosx, -fracpi2+2pi kleq xlt fracpi2+2pi k\ -cosx, fracpi2+2pi kleq xlt frac+2pi k end end 1) Решаем для положительного косинуса (1-я и 4-я четверти) begin frac+1=7frac\ 3(1+tg^2x)+1-7tgx=0\ 3tg^2-7tgx+4=0\ (3tgx-4)(tgx-1)=0\ left[ begin tgx=frac43\ tgx=1 end right. Rightarrow left[ begin x=arctgfrac43+pi k\ x=fracpi4+pi k end right. end
Полученное решение даёт 4 базовых точки на числовой окружности: (fracpi4, arctgfrac43, frac) и (pi+arctgfrac43), которые находятся в 1-й и 3-й четвертях.
Выбираем только точки в 1-й четверти:
(fracpi4) и (arctgfrac43).
Это означает, что в записи решения период будет не (pi k), а (2pi k). begin left[ begin x=arctgfrac43+2pi k\ x=fracpi4+2pi k end right. end2) Решаем для отрицательного косинуса (2-я и 3-я четверти) begin frac+1=-7frac\ 3(1+tg^2x)+1+7tgx=0\ 3tg^2x+7tgx+4=0\ (3tgx+4)(tgx+1)=0\ left[ begin tgx=-frac43\ tgx=-1 end right. Rightarrow left[ begin x=-arctgfrac43+pi k\ x=-fracpi4+pi k end right. end
Полученное решение даёт 4 базовых точки на числовой окружности: (-fracpi4, -arctgfrac43, frac) и (pi-arctgfrac43), которые находятся в 2-й и 4-й четвертях.
Выбираем только точки вo 2-й четверти:
(frac) и (pi-arctgfrac43).
Это означает, что в записи решения будут выбранные точки с периодом (2pi k). begin left[ begin x=pi-arctgfrac43+2pi k\ x=frac+2pi k end right. end3) Объединяем полученные решения: begin left[ begin x=arctgfrac43+2pi k\ x=fracpi4+2pi k\ x=pi-arctgfrac43+2pi k\ x=frac+2pi k end right. end
По аналогии с записью арксинуса можно объединить симметричные относительно оси синусов точки: begin left[ begin x=arctgfrac43+2pi k\ x=pi-arctgfrac43+2pi k end right. Leftrightarrow x=(-1)^k arctgfrac43+pi k\ left[ begin x=fracpi4+2pi k\ x=frac+2pi k end right. Leftrightarrow x=(-1)^k fracpi4+pi k\ end Окончательно получаем: ( left[ begin x=(-1)^k arctgfrac43+pi k\ x=(-1)^k fracpi4+pi k end right. ).
Ответ: ((-1)^k arctgfrac43+pi k, (-1)^k fracpi4+pi k)г) (3sinx-4cosx=5)
Способ 1. Вводим дополнительный угол:
(p=sqrt=5)
(frac35sinx-frac45 cosx=1)
(sinalpha=frac35, cosalpha=frac45)
(sinalpha sinx-cosalpha cosx=1)
(cosalpha cosx-sinalpha sinx=-1)
(cos(x+alpha)=-1)
(x+alpha=pi+2pi k)
(x=-alpha+pi+2pi k=-arcsinfrac35+pi+2pi k)Способ 2. Делаем универсальную подстановку: begin sinalpha=frac<2tgfrac>, cosalpha=frac\ 3cdot frac<2tgfrac><1+tg^2frac>-4cdotfrac<1-tg^2frac><1+tg^2frac>=5\ frac<6tgfrac-4left(1-tg^2fracright)-5left(1+tg^2fracright)><1+tg^2frac>=0 end (1=tg^2fracgeq 1), знаменатель никогда не превращается в 0, отбрасываем его и работаем с числителем: begin -tg^2frac+6tgfrac-9=0Rightarrow tg^2frac-6tgfrac+9=0Rightarrowleft(tgfrac-3right)^2=0Rightarrow tgfrac=3\ frac=arctg3+pi kRightarrow x= 2arctg3+2pi k end
Докажем, что полученные ответы: $$ x=-arcsinfrac35+pi+2pi k text x=2arctg3+2pi k $$ равнозначны, т.е. (-arcsinfrac35+pi=2arctg3), и равны углы: $$ arcsinfrac35=pi-2arctg3 (*) $$ Пусть в правой части равенства (*) (2arctg3=varphi). Тогда (arctg3=fracvarphi2) и (tgfracvarphi2=3).
А в левой части равенства (*) (arcsinfrac35=alpha) и (sinalpha=frac35)
Угол (0lt arcsinfrac35lt fracpi2) расположен в 1-й четверти.
Угол (varphi=2arctg3) расположен во 2-й четверти ((cosvarphilt 0, sinvarphigt 0)). $$ cosvarphi=frac=frac=-frac45, sinvarphi=frac=frac=frac35 $$ Получаем, что для угла (alpha: sinalpha=frac35, cosalpha=frac45)
Для угла (varphi: sinvarphi=frac35, cosvarphi=-frac45)
Откуда следует, что (alpha=pi-varphi). Что и требовалось доказать.
Ответ: (-arcsinfrac35+pi+2pi k) или (2arctg3+2pi k) (т.к. (-arcsinfrac35+pi=2arctg3))Видео:3,5 способа отбора корней в тригонометрии | ЕГЭ по математике | Эйджей из ВебиумаСкачать
РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Простейшими тригонометрическими уравнениями называют уравнения
Чтобы рассуждения по нахождению корней этих уравнений были более наглядными, воспользуемся графиками соответствующих функций.
19.1. Уравнение cos x = a
Объяснение и обоснование
- Корни уравненияcosx=a.
При |a| > 1 уравнение не имеет корней, поскольку |cos x| ≤ 1 для любого x (прямая y = a на рисунке из пункта 1 таблицы 1 при a > 1 или при a 1 уравнение не имеет корней, поскольку |sin x| ≤ 1 для любого x (прямая y = a на рисунке 1 при a > 1 или при a n arcsin a + 2πn, n ∈ Z (3)
2.Частые случаи решения уравнения sin x = a.
Полезно помнить специальные записи корней уравнения при a = 0, a = -1, a = 1, которые можно легко получить, используя как ориентир единичную окружность (рис 2).
Учитывая, что синус равен ординате соответствующей точки единичной окружности, получаем, что sin x = 0 тогда и только тогда, когда соответствующей точкой единичной окружности является точка C или тока D. Тогда
Аналогично sin x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка A, следовательно,
Также sin x = -1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка B, таким образом,
Примеры решения задач
Замечание. Ответ к задаче 1 часто записывают в виде:
19.3. Уравнения tg x = a и ctg x = a
Объяснение и обоснование
1.Корни уравнений tg x = a и ctg x = a
Рассмотрим уравнение tg x = a. На промежутке
функция y = tg x возрастает (от -∞ до +∞). Но возрастающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение tg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арктангенса равен: x1 = arctg a и для этого корня tg x = a.
Функция y = tg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения tg x = a:
При a=0 arctg 0 = 0, таким образом, уравнение tg x = 0 имеет корни x = πn (n ∈ Z).
Рассмотрим уравнение ctg x = a. На промежутке (0; π) функция y = ctg x убывает (от +∞ до -∞). Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение ctg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арккотангенса равен: x1=arсctg a.
Функция y = ctg x периодическая с периодом π, поэтому все остальные корни отличаются от найденного на πn (n ∈ Z). Получаем следующую формулу корней уравнения ctg x = a:
таким образом, уравнение ctg x = 0 имеет корни
Примеры решения задач
Вопросы для контроля
- Какие уравнения называют простейшими тригонометрическими?
- Запишите формулы решения простейших тригонометрических уравнений. В каких случаях нельзя найти корни простейшего тригонометрического уравнения по этим формулам?
- Выведите формулы решения простейших тригонометрических уравнений.
- Обоснуйте формулы решения простейших тригонометрических уравнений для частных случаев.
Упражнения
Решите уравнение (1-11)
Найдите корни уравнения на заданном промежутке (12-13)
💡 Видео
Отбор корней по окружностиСкачать
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать
Отбор корней по окружностиСкачать
Три способа отбора корней в задании 13 ЕГЭ профильСкачать
Учимся объединять корни тригонометрического уравнения. Задание 12 ЕГЭ профильСкачать
Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать
Задание №13. Как отбирать корни в тригонометрической окружности? 🤔Скачать
Как решить пункт б) в задании 13 профиля ЕГЭ. ТригонометрияСкачать
Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать
Тригонометрия 8. Отбор корнейСкачать
10 класс, 23 урок, Методы решения тригонометрических уравненийСкачать
Решение тригонометрических уравнений. Однородные уравнения. 10 класс.Скачать
Отбор корней тригонометрического уравнения с помощью неравенства: пример 1Скачать
Как решать тригонометрические неравенства?Скачать
ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ - Решение Тригонометрических уравнений / Подготовка к ЕГЭ по МатематикеСкачать
Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать
Решение тригонометрических уравнений. Метод понижения порядка. 10 класс.Скачать
Выборка с помощью окружностиСкачать
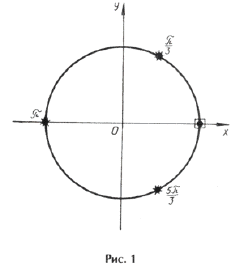
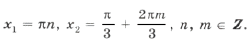
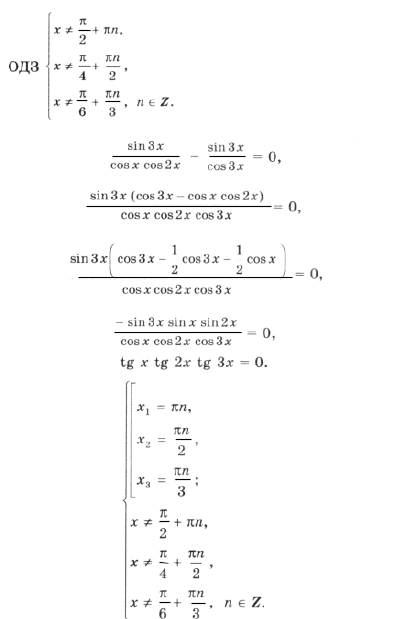
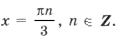
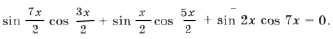
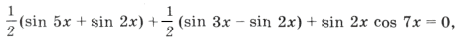
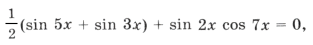
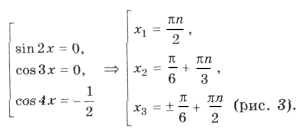
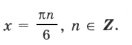
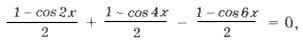
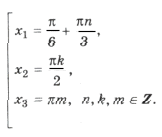
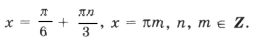
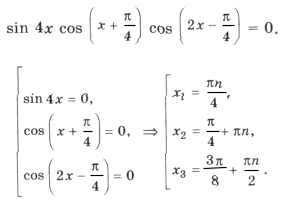
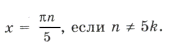
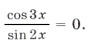
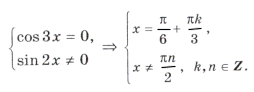
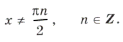
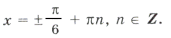
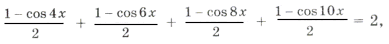
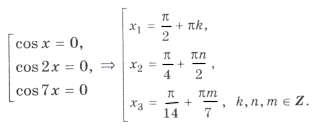
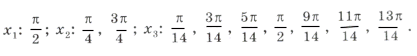
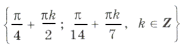
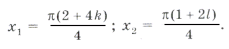
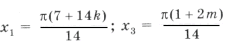
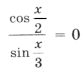
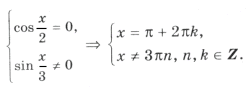
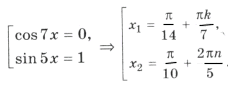
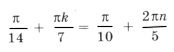
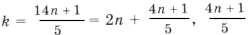 – целое число.
– целое число.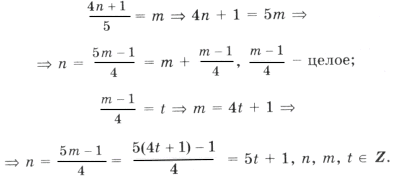
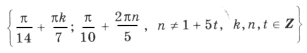 .
.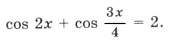
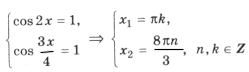
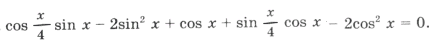
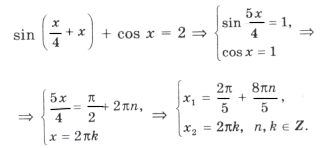
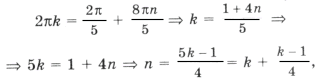 ,
,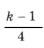 – целое число;
– целое число;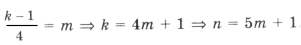
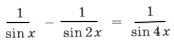
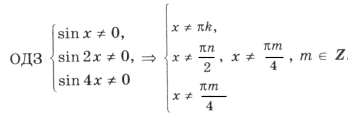
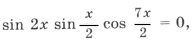
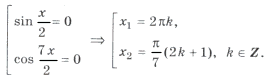
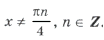
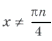 ,
,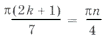 ,
,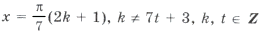
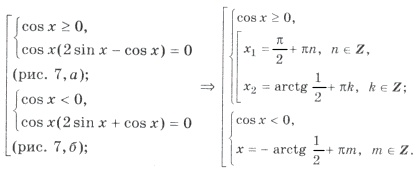

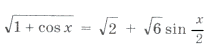
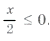
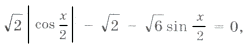
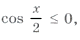 то
то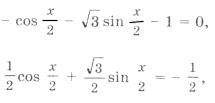
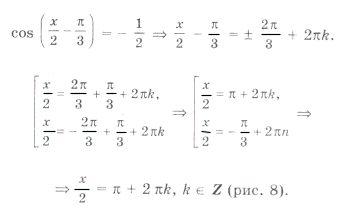
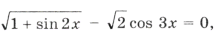
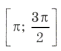 .
.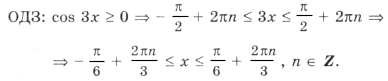
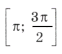 принадлежит только один промежуток из ОДЗ, а именно
принадлежит только один промежуток из ОДЗ, а именно 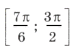 .
.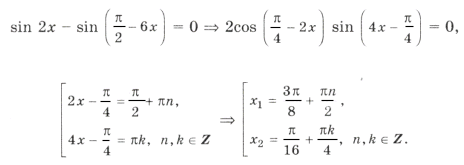
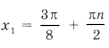 при n = 2 имеем
при n = 2 имеем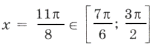
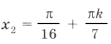 при n = 5 имеем
при n = 5 имеем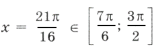
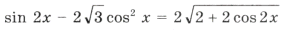
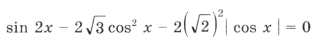
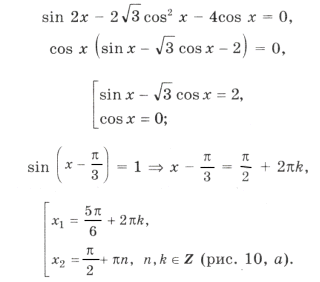
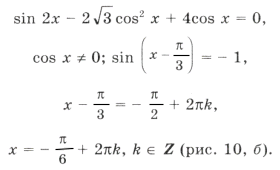
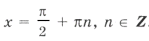
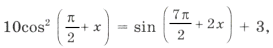
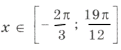 .
.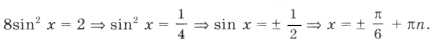
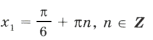
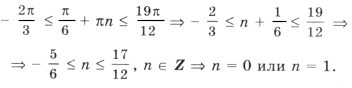
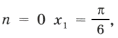
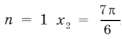 .
.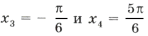 .
.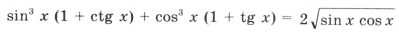
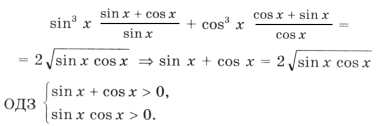
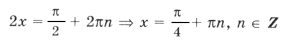
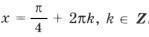
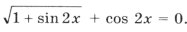
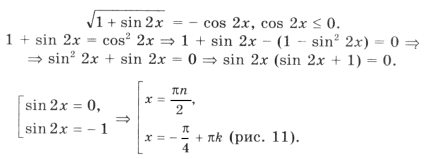
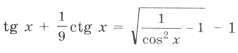
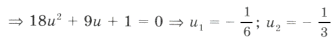
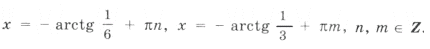
 .
.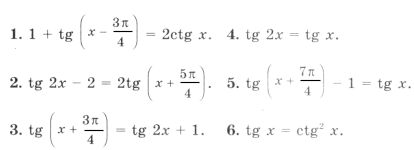
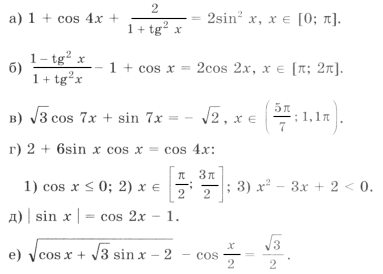






















 функция y = tg x возрастает (от -∞ до +∞). Но возрастающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение tg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арктангенса равен: x1 = arctg a и для этого корня tg x = a.
функция y = tg x возрастает (от -∞ до +∞). Но возрастающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение tg x = a при любом значении a имеет на этом промежутке только один корень, который по определению арктангенса равен: x1 = arctg a и для этого корня tg x = a.


























