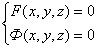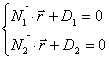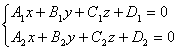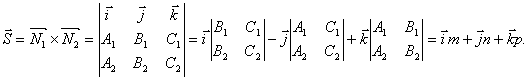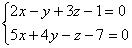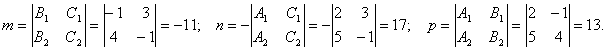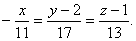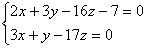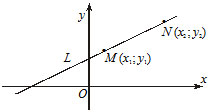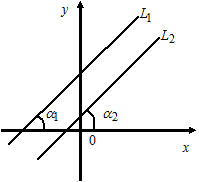Найти направляющие косинусы прямой заданной уравнением (2 видео)

Найти направляющие косинусы прямой заданной уравнением

Уравнение линии в пространстве.

Как на плоскости, так и в пространстве, любая линия может быть определена как совокупность точек, координаты которых в некоторой выбранной в пространстве системе координат удовлетворяют уравнению:

Это уравнение называется уравнением линии в пространстве.

Кроме того, линия в пространстве может быть определена и иначе. Ее можно рассматривать как линию пересечения двух поверхностей, каждая из которых задана каким- либо уравнением.

Пусть F ( x , y , z ) = 0 и Ф ( x , y , z ) = 0 – уравнения поверхностей, пересекающихся по линии L .

Тогда пару уравнений

назовем уравнением линии в пространстве.

Содержание

Математический портал
Nav view search
Navigation
Search
Аналитическая геометрия.
Прямая на плоскости, всевозможные уравнения.
Деление отрезка в заданном отношении (векторный и координатный способы).
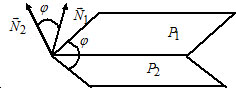
Взаимное расположение плоскостей, угол между плоскостями.
Направляющий вектор прямой, координаты направляющего вектора прямой
Что такое направляющий вектор прямой
Как вычислить координаты направляющего вектора по уравнениям прямой
📹 Видео

Уравнение прямой в пространстве по точке и

Возьмем произвольную прямую и вектор ( m , n , p ), параллельный данной прямой. Вектор называется направляющим вектором прямой.

На прямой возьмем две произвольные точки М ₀ ( x ₀ , y ₀ , z ₀ ) и M ( x , y , z ).

M ₁

Обозначим радиус- векторы этих точек как и , очевидно, что — = .

Т.к. векторы и коллинеарны , то верно соотношение = t , где t – некоторый параметр.

Итого, можно записать: = + t .

Т.к. этому уравнению удовлетворяют координаты любой точки прямой, то полученное уравнение – параметрическое уравнение прямой.

Это векторное уравнение может быть представлено в координатной форме:

Преобразовав эту систему и приравняв значения параметра t , получаем канонические уравнения прямой в пространстве:

Определение. Направляющими косинусами прямой называются направляющие косинусы вектора , которые могут быть вычислены по формулам:

; .

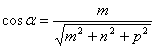
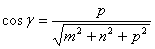
Отсюда получим: m : n : p = cos a : cos b : cos g .

Числа m , n , p называются угловыми коэффициентами прямой. Т.к. — ненулевой вектор, то m , n и p не могут равняться нулю одновременно, но одно или два из этих чисел могут равняться нулю. В этом случае в уравнении прямой следует приравнять нулю соответствующие числители.

Уравнение прямой в пространстве, проходящей

через две точки.

Если на прямой в пространстве отметить две произвольные точки M ₁( x ₁, y ₁, z ₁) и M ₂( x ₂, y ₂, z ₂), то координаты этих точек должны удовлетворять полученному выше уравнению прямой:

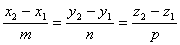
Кроме того, для точки М ₁ можно записать:

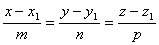
Решая совместно эти уравнения, получим:

Это уравнение прямой, проходящей через две точки в пространстве.

Общие уравнения прямой в пространстве.

Уравнение прямой может быть рассмотрено как уравнение линии пересечения двух плоскостей.

Как было рассмотрено выше, плоскость в векторной форме может быть задана уравнением:

× + D = 0, где

— нормаль плоскости; — радиус- вектор произвольной точки плоскости.

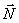
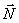
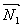
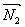
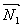
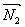
Пусть в пространстве заданы две плоскости: × + D ₁ = 0 и × + D ₂ = 0, векторы нормали имеют координаты: ( A ₁ , B ₁ , C ₁ ), ( A ₂ , B ₂ , C ₂ ); ( x , y , z ).

Тогда общие уравнения прямой в векторной форме:

Общие уравнения прямой в координатной форме:

Практическая задача часто состоит в приведении уравнений прямых в общем виде к каноническому виду.

Для этого надо найти произвольную точку прямой и числа m , n , p .

При этом направляющий вектор прямой может быть найден как векторное произведение векторов нормали к заданным плоскостям.

Пример. Найти каноническое уравнение, если прямая задана в виде:

Для нахождения произвольной точки прямой, примем ее координату х = 0, а затем подставим это значение в заданную систему уравнений.

, т.е. А(0, 2, 1).

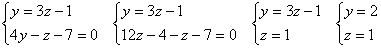
Находим компоненты направляющего вектора прямой.

Тогда канонические уравнения прямой :

Пример. Привести к каноническому виду уравнение прямой, заданное в виде:

Для нахождения произвольной точки прямой, являющейся линией пересечения указанных выше плоскостей, примем z = 0. Тогда :

;

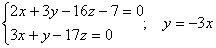
Получаем: A ( -1; 3; 0).

Направляющий вектор прямой: .

Итого:

Видео:§7 Направляющие косинусы вектораСкачать

Математический портал

Видео:#вектор Разложение вектора по ортам. Направляющие косинусыСкачать

Nav view search

Search

Вы здесь:
Home
Векторная алгебра.
Проекции вектора. Направляющие косинусы. Неравенство Коши-Буняковского.
Высшая математика.
Аналитическая геометрия.

Видео:задача на направляющие косинусыСкачать

Аналитическая геометрия.

Видео:Видеоурок "Нормальное уравнение прямой"Скачать

Прямая на плоскости, всевозможные уравнения.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Существуют такие формы записи уравнения прямой:

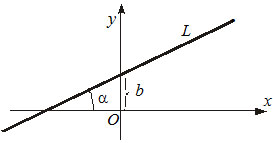
1) $y=kx+b,$ где $k -$ угловой коэффициент, $b-$ отрезок, который прямая отсекает на оси $OY.$

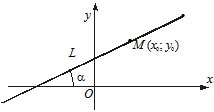
2) $y-y_0=k(x-x_0) $ — уравнение прямой, которая проходит через заданную точку $P(x_0, y_0)$ под заданным углом $alpha$ к оси $OX$ $(k=tgalpha).$

3) $frac=frac $ — уравнение прямой, которая проходит через две точки $M(x_1, y_1)$ и $N(x_2, y_2).$

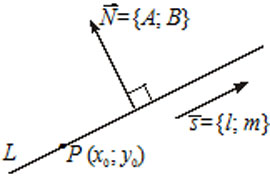
5) $frac=frac $ — каноническое уравнение прямой, где $overline~~=(l, m) -$ направляющий вектор прямой, то есть вектор параллельный прямой $(overline~~parallel L),$ точка $P(x_0, y_0)in L.$~~~~

6) $A(x-x_0)+B(y-y_0)=0$ — уравнение прямой $L,$ которая проходит через точку $M(x_0, y_0)$ перпендикулярно вектору $overline=(A, B).$ Вектор $overline N$ называется нормальным вектором прямой.

~~7) $Ax+By+C=0 -$ общее уравнение прямой $L,$ где $overline=(A, B) -$ нормальный вектор прямой $L.$~~

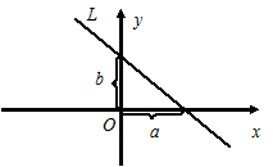
8) $xcosalpha+ycosbeta-p=0 -$ нормальное уравнение прямой, где $cosalpha$ и $cosbeta -$ направляющие косинусы нормального вектора $n,$ направленного из начала координат в сторону прямой, а $p>0 -$ расстояние от начала координат до прямой.

~~Общее уравнение прямой приводится к нормальному, путем умножения на нормирующий множитель $mu=-frac<sqrt>.$~~

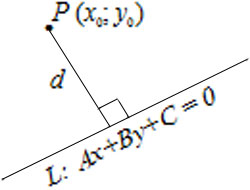
Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=left|frac<sqrt >right|.$$

~~Расположение двух прямых на плоскости.~~

~~Условия параллельности двух прямых:~~

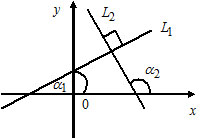
~~1) Пусть $L_1: k_1x+b_1,$ $k_1=tgalpha_1;$~~

~~$L_2: k_2x+b_2,$ $k_2=tgalpha_2.$~~

~~Прямые $L_1$ и $L_2$ параллельны тогда и только тогда, когда $k_1=k_2.$~~

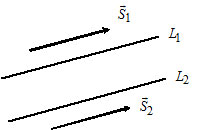
~~2) Пусть $L_1:$ $frac=frac,$ $overline~~_1=(l_1, m_1);$~~~~

~~Прямые $L_1$ и $L_2$ параллельны тогда и только тогда, когда $overline~~_1paralleloverline~~_2Leftrightarrow$ $frac=frac.$~~~~~~

~~3) Пусть $L_1: A_1x+B_1y+C_1=0,$ $overline_1=(A_1, B_1);$~~

~~$L_2: A_2x+B_2y+C_2=0,$ $overline_2=(A_2, B_2).$~~

~~Прямые $L_1$ и $L_2$ параллельны тогда и только тогда, когда $overline_1paralleloverline_2Leftrightarrow$ $frac~~~~=frac.$~~

~~Условия перпендикулярности двух прямых:~~

~~1) Пусть $L_1: k_1x+b_1,$ $k_1=tgalpha_1;$~~

~~$L_2: k_2x+b_2,$ $k_2=tgalpha_2.$~~

~~$L_1perp L_2Leftrightarrow$ $k_1cdot k_2=-1.$~~

~~2) Пусть $L_1:$ $frac=frac,$ $overline~~_1=(l_1, m_1);$~~~~

~~~~$L_1perp L_2Leftrightarrow$ $overline~~_1perpoverline~~_2Leftrightarrow$ $cdot+cdot=0.$~~~~~~~~

~~3) Пусть $L_1: A_1x+B_1y+C_1=0,$ $overline_1=(A_1, B_1);$~~

~~$L_2: A_2x+B_2y+C_2=0,$ $overline_2=(A_2, B_2).$~~

~~$L_1perp L_2Leftrightarrow$ $overline_1perpoverline_2Leftrightarrow$ $~~cdot +cdot=0.$

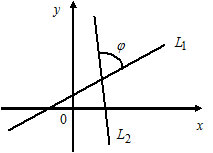
~~Угол между прямыми:~~

~~1) Пусть $L_1: k_1x+b_1,$ $k_1=tgalpha_1;$~~

~~$L_2: k_2x+b_2,$ $k_2=tgalpha_2.$~~

~~2) Пусть $L_1:$ $frac=frac,$ $overline~~_1=(l_1, m_1);$~~~~

~~~~3) Пусть $L_1: A_1x+B_1y+C_1=0,$ $overline_1=(A_1, B_1);$~~~~

~~~~$L_2: A_2x+B_2y+C_2=0,$ $overline_2=(A_2, B_2).$~~~~

~~~~Примеры:~~~~

~~~~2.141.~~~~

а) Прямая $L$ задана точкой $M_0(-1; 2)in L$ и нормальным вектором $overline N(2; 2).$ Требуется: 1) написать уравнение прямой, привести его к общему виду и построить прямую; 2) привести общее уравнение к нормальному виду и указать расстояние от начала координат до прямой.

~~~~Решение.~~~~

Подставим в формулу 6) для уравнения прямых ( $A(x-x_0)+B(y-y_0)=0$ ) соответственно координаты точки $(x_0; y_0)=M_0(-1; 2)$ и вектора $(A; B)=overline N(2; 2):$

~~~~$2(x+1)+2(y-2)=0.$ Далее, приведем это уравнение к общему виду:~~~~

Нормальное уравнение прямой имеет вид $xcosalpha+ycosbeta-p=0,$ где $cosalpha$ и $cosbeta -$ направляющие косинусы нормального вектора $n,$ направленного из начала координат в сторону прямой, а $p>0 -$ расстояние от начала координат до прямой.

~~Общее уравнение прямой приводится к нормальному, путем умножения на нормирующий множитель $mu=-frac<sqrt~~~~>.$~~

~~~~Для нашей прямой имеем $A=1; B=1; C=-1 Rightarrow sgn C=-1.$ Таким образом, $mu=-frac<sqrt>=frac.$~~~~

~~~~Запишем нормальное уравнение прямой:~~~~

~~~~Расстояние от начала координат $p=frac.$~~~~

Ответ: $2(x+1)+2(y-2)=0;$ общее уравнение $x+y-1=0;$ нормальное уравнение прямой $fracx+fracy-frac=0;$ $p=frac.$

~~~~2.142.~~~~

а) Прямая $L$ задана точкой $M_0(-1; 2)in L$ и направляющим вектором $overline S(3; -1).$ Требуется: 1) написать уравнение прямой, привести его к общему виду и построить прямую; 2) привести общее уравнение к нормальному виду и указать расстояние от начала координат до прямой.

~~~~Решение.~~~~

Подставим в формулу 5) для уравнения прямых ( $frac=frac$ ) соответственно координаты точки $(x_0; y_0)=M_0(-1; 2)$ и вектора $(l; m)=overline S(3; -1):$ $frac=frac$

~~~~Далее, приведем это уравнение к общему виду:~~~~

~~~~Общее уравнение прямой приводится к нормальному, путем умножения на нормирующий множитель $mu=-frac<sqrt >.$~~~~

~~~~Для нашей прямой имеем $A=1; B=3; C=-5 Rightarrow sgn C=-1.$ Таким образом, $mu=-frac<sqrt>=frac<sqrt>.$~~~~

~~~~Запишем нормальное уравнение прямой:~~~~

~~~~Расстояние от начала координат $p=frac<sqrt >.$~~~~

Ответ: $frac=frac;$ общее уравнение $x+3y-5=0;$ нормальное уравнение прямой $frac<sqrt >x+frac<sqrt >y-frac<sqrt >=0;$ $p=frac<sqrt >.$

~~~~2.143.~~~~

а) Прямая $L$ задана двумя своими точками $M_1(1; 2)in L$ и $M_2(-1; 0)in L.$ Требуется: 1) написать уравнение прямой, привести его к общему виду и построить прямую; 2) привести общее уравнение к нормальному виду и указать расстояние от начала координат до прямой.

~~~~Решение.~~~~

Подставим в формулу 3) для уравнения прямых ($frac=frac$ ) соответственно координаты точек $M_1(1; 2)= (x_1; y_1) $ и $M_2(-1; 0)=(x_2; y_2):$ $frac=fracRightarrow frac=frac.$

~~~~Далее, приведем это уравнение к общему виду:~~~~

~~~~Для нашей прямой имеем $A=1; B=-1; C=1 Rightarrow sgn C=1.$ Таким образом, $mu=-frac<sqrt>=-frac<sqrt>.$~~~~

~~~~Запишем нормальное уравнение прямой:~~~~

~~~~Расстояние от начала координат $p=frac<sqrt >.$~~~~

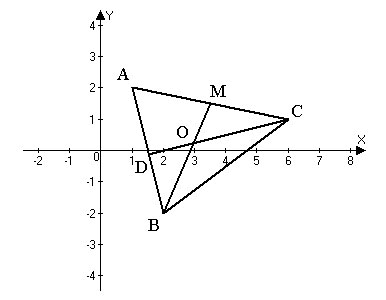
2.150. Треугольник $ABC$ задан координатами своих вершин $A(1; 2), B(2; -2), C(6; 1).$ Требуется:

~~~~1) Найти уравнение стороны $AB;$~~~~

~~~~2) найти уравнение высоты $CD$ и вычислить ее длину $h=|CD|;$~~~~

~~~~3) найти угол между высотой $CD$ и медианой $BM.$~~~~

~~~~Решение.~~~~

~~~~1) Уравнение прямой $AB$ найдем по формуле уравнения прямой, проходящей через две точки $frac=frac. $~~~~

~~~~В нашем случае $(x_1; y_1)=A(1; 2);$ $(x_2; y_2)=B(2; -2).$~~~~

Подставляем координаты точек в уравнение прямой. Получаем $$frac=fracRightarrow x-1=frac.$$ Запишем общее уравнение прямой $AB$:

~~~~$-4(x-1)=y-2Rightarrow$ $-4x+4=y-2Rightarrow$ $4x+y-6=0.$~~~~

2) Уравнение прямой $CD$ найдем, пользуясь уравнением ( 6): $A(x-x_0)+B(y-y_0)=0$ — уравнение прямой $L,$ которая проходит через точку $M(x_0, y_0)$ перпендикулярно вектору $overline=(A, B).$

~~~~В нашем случае, высота $CD$ это прямая, которая проходит через точку $C$ перпендикулярно вектору $AB.$~~~~

~~~~Таким образом, $$(x_0; y_0)=C=(6; 1);quadoverline=overline=(2-1; -2-2)=(1; -4).$$~~~~

~~~~Подставляем эти координаты в уравнение прямой:~~~~

~~~~$1(x-6)-4(y-1)=0Rightarrow x-6-4y+4=0 Rightarrow x-4y-2=0.$~~~~

~~~~То есть, уравнение прямой $CD:$ $x-4y-2=0.$~~~~

~~~~Чтобы найти длину высоты $h=|CD|,$ найдем координаты точки $D,$ как точки пересечения прямых $CD$ и $AB:$~~~~

~~~~Решим систему методом исключений:~~~~

~~~~Следовательно имеем $D(26/17; -2/17).$ Теперь можем найти длину высоты $CD:$~~~~

3) Уравнение высоты $CD$ мы уже нашли в пункте 2). Найдем уравнение медианы $BM.$ Будем его искать, используя форумулу уравнения прямой, проходящей через две точки.

~~~~Координаты точки $B=(2, -2); $ координаты точки $M$ найдем как середину стороны $AC:$ $x_M=frac; y_M=frac.$~~~~

~~~~Подставляем координаты точек $B(2; -2)$ и $M(3.5; 1.5)$ в уравнение прямой~~~~

~~~~$3.5(x-2)=1.5(y+2)Rightarrow 3.5x-7=1.5y+3 Rightarrow 3.5x-1.5y-10=0.$~~~~

~~~~Далее, зная общие уравнения двух прямых $CD: x-4y-2=0$ и $BM: 3.5x-1.5y-10=0$ можно найти угол между ними по формуле~~~~

~~~~где $L_1: A_1x+B_1y+C_1=0,$ $overline_1=(A_1, B_1);$~~~~

~~~~$L_2: A_2x+B_2y+C_2=0,$ $overline_2=(A_2, B_2).$~~~~

~~~~Для наших прямых имеем: $(A_1, B_1)=(1; -4);$ $(A_2; B_2)=(3.5; -1.5).$~~~~

Ответ: 1) $AB: 4x+y-6=0.$

2.160. В равнобедренном треугольнике $ABC$ заданы вершина $C(4; 3),$ уравнение $2x-y-5=0$ основания $AC$ и уравнение $x-y=0$ боковой стороны $AB.$ Найти уравнение стороны $BC.$

~~~~Решение.~~~~

~~~~Найдем координаты вершины треугольника $A,$ как точки пересечения прямых $AB$ и $AC:$~~~~

Таким образом, мы имеем координаты вершин при основании равнобедренного треугольника $A(5; 5)$ и $C(4; 3).$ Найдем координаты вершины $B(x, y).$ Мы знаем, что эта точка принадлежит прямой $AB: x-y=0$ и что $AB=BC.$ Запишем формулы для длин сторон $AB$ и $BC:$

~~~~Далее, чтобы найти координаты точки $B,$ решим систему уравнений:~~~~

~~~~$$Rightarrowleft<beginx=y\y=frac.endright.$$ Мы нашли координаты точки $Bleft(frac, fracright).$~~~~

Зная координаты точек $B$ и $C$ можно записать уравнение прямой $BC,$ как прямой проходящей через две точки $left(frac=frac right):$

~~~~$$Rightarrowfrac=fracRightarrow 7x-28=y-3Rightarrow 7x-y-25=0.$$~~~~

Ответ: $7x-y-25=0.$

2.165. Даны две противоположные вершины квадрата $A(1; 3)$ и $C(-1; 1).$ Найти координаты двух его других вершин и написать уравнения его сторон.

~~~~Решение:~~~~

~~~~Найдем уравнение диагонали $AC:$~~~~

Далее, найдем уравнение второй диагонали квадрата — прямой, проходящей через точку $O$ перпендикулярно прямой $AC.$ Для прямой $AC$ нормальный вектор имеет координаты $overline=(1; -1).$ Прямая, перпендикулярная прямой $AC$ является параллельной нормальному вектору $overline$. Таким образом, уравнение прямой $BD$ запишем по формуле 5) $left(frac=fracright),$ где $(x_0, y_0)=O(0; 2),$ $(l, m)=overline=(1, -1):$

~~~~$$frac=fracRightarrow x=-y+2 Rightarrow x+y-2=0.$$~~~~

~~~~Ясно, что $AO=CO=BO=DO.$ Найдем длину отрезка $AO:$ $AO=sqrt=sqrt.$~~~~

~~~~Далее, будем искать координаты точек $B$ и $D,$ принадлежащих прямой $BD$ и таких, что $BO=DO=AO.$~~~~

Таким образом, мы нашли координаты вершин $B(1; 1)$ и $D(-1; 3).$ Зная координаты вершин квадрата, запишем уравнения его сторон, пользуясь формулой ( 3) — $frac=frac $ — уравнение прямой, которая проходит через две точки $M(x_1, y_1)$ и $N(x_2, y_2).$

Ответ: $A(1; 3),$ $B(1; 1),$ $C(-1; 1),$ $D(-1; 3);$ $AB:$ $x=1;$ $BC:$ $y=1;$ $CD:$ $x=-1;$ $DA:$ $y=3.$

~~~~Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать~~~~

Деление отрезка в заданном отношении (векторный и координатный способы).

~~~~Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.~~~~

Зная координаты точек $M_1(x_1, y_1, z_1)$ и $M_2(x_2, y_2, z_2)$ и отношение $lambda,$ в котором точка $M$ делит направленный отрезок $overline,$ найдем координаты точки $M.$

Пусть $O -$ начало координат. Обозначим $overline=r_1,$ $overline=r_2,$ $overline=r.$ Так как, $$overline=r-r_1, overline=r_2-r,$$ то $r-r_1=lambda(r_2-r),$ откуда (так как $lambdaneq -1$) $$r=frac.$$ Полученная форма и дает решение задачи в векторной форме. Переходя в этой формуле к координатам, получим $$x=frac, y=frac, z=frac.$$

~~~~Примеры.~~~~

2.57. Отрезок с концами в точках $A(3, -2)$ и $B(6, 4)$ разделен на три равные части. Найти координаты точек деления.

~~~~Решение.~~~~

Пусть $C(x_C, y_C)$ и $D(x_D, y_D) -$ точки, которые делят отрезок $AB$ на три равные части. Тогда $$lambda_1=frac=frac;$$ $$x_C=frac=frac<3+fraccdot 6><1+frac>=4;$$

~~~~Далее находим координаты точки $D:$~~~~

Ответ: $(4, 0)$ и $(5, 2).$

~~~~2.58. Определить координаты концов отрезка, который точками $C(2, 0, 2)$ и $D(5, -2, 0)$ разделен на три равные части.~~~~

~~~~Решение.~~~~

~~~~Пусть $A(x_A, y_A, z_A)$ и $B(x_B, y_B, z_B) -$ концы заданного отрезка.~~~~

~~~~Выпишем формулы для нахождения координат точки $C$ и подставим известные координаты:~~~~

~~~~Аналогичные равенства запишем для точки $D:$~~~~

~~~~Далее запишем полученные уравнения относительно $x_A, x_B;$ $y_A, y_B$ и $z_A, z_B$ попарно в виде систем и решим их:~~~~

~~~~Таким образом, получили координаты концов отрезка $A(-1, 2, 4)$ и $B(8, -4, -2).$~~~~

Ответ: $A(-1, 2, 4),$ $B(8, -4, -2).$

~~~~Видео:Геометрия. 9 класс. Уравнение прямой. Направляющий вектор и вектор нормали прямой /22.10.2020/Скачать~~~~

Взаимное расположение плоскостей, угол между плоскостями.

~~~~Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.~~~~

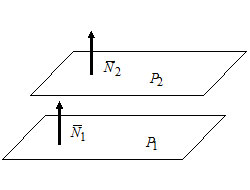
~~~~Условие параллельности двух плоскостей:~~~~

~~~~Пусть $P_1: A_1x+B_1y+C_1z+D_1=0,$ $overline_1=(A_1, B_1, C_1);$~~~~

~~~~$P_2: A_2x+B_2y+C_2z+D_2=0,$ $overline_2=(A_2, B_2, C_2).$~~~~

~~~~Плоскости $P_1$ и $P_2$ параллельны тогда и только тогда, когда $overline_1paralleloverline_2Leftrightarrow$ $frac =frac=frac.$~~~~

~~~~Условия перпендикулярности двух плоскостей:~~~~

~~~~Пусть $P_1: A_1x+B_1y+C_1z+D_1=0,$ $overline_1=(A_1, B_1, C_1);$~~~~

~~~~$P_2: A_2x+B_2y+C_2z+D_2=0,$ $overline_2=(A_2, B_2, C_2).$~~~~

~~~~$P_1perp P_2Leftrightarrow$ $overline_1perpoverline_2Leftrightarrow$ $cdot +cdot+C_1cdot C_2=0.$~~~~

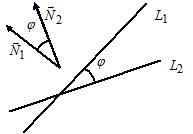
~~Угол между плоскостями:~~

~~Пусть $P_1: A_1x+B_1y+C_1z+D_1=0,$ $overline_1=(A_1, B_1, C_1);$~~

~~$P_2: A_2x+B_2y+C_2z+D_2=0,$ $overline_2=(A_2, B_2, C_2).$~~

~~Примеры.~~

В задачах исследовать взаимное расположение заданных плоскостей. При этом, в случае $P_1parallel P_2$ то найти расстояние между плоскостями, а в случае — косинус угла между ними.

2.185. $P_1: -x+2y-z+1=0;$ $P_2: y+3z-1=0.$

~~Решение.~~

~~Вычислим угол между заданными плоскостями.~~

~~$P_1: -x+2y-z+1=0, Rightarrowoverline_1=(-1, 2, -1);$~~

~~$P_2: y+3z-1=0, Rightarrowoverline_2=(0, 1, 3).$~~

~~Соответственно, плоскости пересекаются и косинус кратчайшего угла между плоскостями~~

Ответ: Плоскости пересекаются. $coswidehat=frac<2sqrt>.$

~~Решение.~~

~~Вычислим угол между заданными плоскостями.~~

~~$P_1: x-y+1=0, Rightarrowoverline_1=(1, -1, 0);$~~

~~$P_2: y-z+1=0, Rightarrowoverline_2=(0, 1, -1).$~~

~~Соответственно, плоскости пересекаются и косинус кратчайшего угла между плоскостями~~

Ответ: Плоскости пересекаются. $coswidehat=frac.$

2.196. Составить уравнение плоскости $P,$ проходящей через точку $A(1, 1, -1)$ и перпендикулярной к плоскостям $P_1: 2x-y+5z+3=0$ и $P_2: x+3y-z-7=0.$

~~Решение.~~

Для того, чтобы плоскость $P$ была перпендикулярно плоскостям $P_1$ и $P_2,$ достаточно, чтобы она была параллельна их нормалям $N_1$ и $N_2.$ Или, что тоже самое, перпендикулярна векторному произведению $[N_1, N_2]$

~~$P_1: 2x-y+5z+3=0, Rightarrowoverline_1=(2, -1, 5);$~~

~~$P_2: x+3y-z-7=0, Rightarrowoverline_2=(1, 3, -1).$~~

Теперь выпишем уравнение плоскости, проходящей через заданную точку $A(1, 1, -1)$ и перпендикулярной вектору $[N_1, N_2]=(-14, 7, 7):$

Ответ: $-2x+y+z+2=0.$

~~Домашнее задание.~~

~~Видео:Угол между векторами | МатематикаСкачать~~

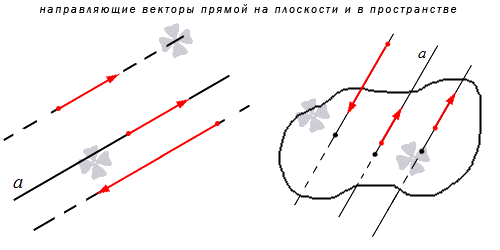
Направляющий вектор прямой, координаты направляющего вектора прямой

С понятием прямой линии тесно связано понятие ее направляющего вектора. Часто в задачах бывает удобнее рассматривать его вместо самой прямой. В рамках данного материала мы разберем, что же такое направляющий вектор прямой в пространстве и на плоскости, и расскажем, для чего можно его использовать.

В первом пункте мы сформулируем определение и покажем основные понятия на иллюстрациях, дополнив их конкретными примерами направляющего вектора. Далее мы посмотрим, как прямая и направляющие векторы взаимодействуют в прямоугольной системе координат и как можно вычислить координаты этого вектора, если мы знаем уравнение прямой. Все правила, как всегда, будут проиллюстрированы примерами решений задач.

~~Видео:Найти сумму направляющих косинусов вектораСкачать~~

Что такое направляющий вектор прямой

Для того чтобы понять эту тему, нам нужно хорошо представлять, что такое вообще прямая и как она может размещаться в пространстве и на плоскости. Кроме того, важно вспомнить ранее изученное понятие вектора. Об этом мы уже писали в отдельном материале. Если нужно, найдите и перечитайте эти статьи.

~~Сформулируем, что такое направляющий вектор.~~

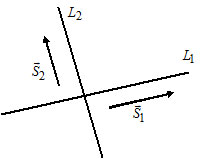
Направляющим вектором прямой является любой вектор, не равный нулю, который размещается на данной прямой или же на прямой, параллельной ей.

Получается, что у каждой прямой есть бесконечное множество направляющих векторов. При этом все они будут являться коллинеарными в силу озвученного определения, ведь они лежат на одной прямой или параллельной ей другой прямой. Выходит, что если a → является направляющий вектором прямой a , то другой направляющий вектор мы можем обозначить как t · a → при любом значении t , соответствующем действительному числу.

Также из определения выше можно сделать вывод, что направляющие векторы двух параллельных прямых будут совпадать: если прямые a и a 1 являются параллельными, то вектор a → будет направляющим и для a , и для a 1 .

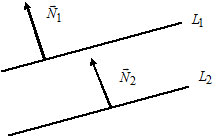
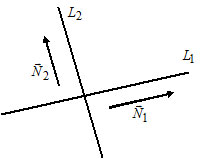
Третий вывод, следующий из определения: если у нас есть направляющий вектор прямой a , то он будет перпендикулярным по отношению к любому нормальному вектору той же прямой.

Приведем пример направляющего вектора: в прямоугольной системе координат для осей O x , O y и O z направляющими будут координатные векторы i → , j → и k → .

~~Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать~~

Как вычислить координаты направляющего вектора по уравнениям прямой

Допустим, что у нас есть некая прямая с направляющими векторами, лежащая в прямоугольной системе координат. Сначала мы разберем случай с плоской декартовой системой O x y , а потом с системой O x y z , расположенной в трехмерном пространстве.

1. Прямую линию в O x y можно описать с помощью уравнения прямой на плоскости. В этом случае координаты направляющих векторов будут соответствовать направляющим векторам исходной прямой. А если нам известно уравнение прямой, как вычислить координаты ее направляющего вектора? Это легко сделать, если мы имеем дело с каноническим или параметрическим уравнением.

Допустим, у нас есть канонический случай уравнения, которое имеет вид x — x 1 a x = y — y 1 a y . С его помощью на плоскости задана прямая с направляющим вектором a → = ( a x , a y ) .

Чтобы вычислить координаты направляющего вектора, нам нужно взять числа из знаменателя канонического уравнения прямой.

~~Приведем пример задачи.~~

В прямоугольной системе координат задана прямая, которую можно описать уравнением x — 1 4 = y + 1 2 — 3 . Вычислите координаты одного из направляющих векторов прямой.

~~Решение~~

Из уравнения мы можем сразу взять координаты направляющего вектора. Берем числа в знаменателях и записываем: 4 , — 3 . Это и будет нужный нам ответ.

Ответ: 4 , — 3 .

Если же прямая описана уравнением параметрического типа, то нам нужно смотреть на коэффициенты при параметре. Они будут соответствовать координатам нужного нам направляющего вектора.

У нас есть прямая, которую можно описать с помощью системы параметрических уравнений x = — 1 y = 7 — 5 · λ , при этом λ ∈ R . Найдите координаты направляющих векторов.

~~Решение~~

Для начала перепишем данные параметрические уравнения в виде x = — 1 + 0 · λ y = 7 — 5 · λ . Посмотрим на коэффициенты. Они сообщат нам нужные координаты направляющего вектора – a → = ( 0 , 5 ) . Учитывая, что все направляющие векторы одной прямой будут коллинеарны, мы можем задать их в виде t · a → или 0 , — 5 · t , где t может быть любым действительным числом. О том, как проводить действия с векторами в координатах, мы писали в отдельной статье.

Ответ: 0 , — 5 · t , t ∈ R , t ≠ 0

Теперь разберем случай, как найти координаты вектора, если прямая задана общим уравнением вида A x + B y + C = 0 . Если A = 0 , то исходное уравнение можно переписать как B y + C = 0 . Оно определяет прямую, которая будет параллельна оси абсцисс. Значит, в качестве ее направляющего вектора мы можем взять координатный вектор i → = 1 , 0 .

А если B = 0 , то уравнение прямой мы можем записать как A x + C = 0 . Описываемая им прямая будет параллельна оси ординат, поэтому ее координатный вектор j → = 0 , 1 также будет направляющим. Рассмотрим конкретную задачу.

У нас есть прямая, заданная при помощи общего уравнения x — 2 = 0 . Найдите координаты любого направляющего вектора.

~~Решение~~

В прямоугольной системе координат исходное уравнение будет соответствовать прямой, параллельной оси ординат. Значит, мы можем взять координатный вектор j → = ( 0 , 1 ) . Он будет для нее направляющим.

Ответ: ( 0 , 1 )

А как быть в случае, если ни один коэффициент в A x + B y + C = 0 не будет равен 0? Тогда мы можем использовать несколько разных способов.

1. Мы можем переписать основное уравнение так, чтобы оно превратилось в каноническое. Тогда координаты вектора можно будет взять из его значений.

2. Можно вычислить отдельно начальную и конечную точку направляющего вектора. Для этого надо будет взять координаты двух любых несовпадающих точек исходной прямой.

3. Третий способ заключается в вычислении координат любого вектора, который будет перпендикулярен нормальному вектору этой прямой n → = A , B .

~~Самым простым является первый подход. Проиллюстрируем его на примере задачи.~~

Есть прямая на плоскости, заданная уравнением 3 x + 2 y — 10 = 0 . Запишите координаты любого направляющего вектора.

~~Решение~~

Перепишем исходное уравнение в каноническом виде. Сначала перенесем все слагаемые из левой части, кроме 3 x, в правую с противоположным знаком. У нас получится:

~~3 x + 2 y — 10 = 0 ⇔ 3 x = — 2 y + 10~~

~~Получившееся равенство преобразовываем и получаем:~~

~~3 x = — 2 y + 10 ⇔ 3 x = — 2 ( y — 5 ) ⇔ x — 2 = y — 5 3~~

~~Отсюда мы уже можем вывести координаты нужного нам направляющего вектора: -2 , 3~~

К общему виду легко свести и такие типы уравнений, как уравнение прямой в отрезках x a + y b = 1 и уравнение прямой с угловым коэффициентом y = k · x + b , так что если они встретились вам в задаче на нахождение координат направляющего вектора, то можно также использовать этот подход.

~~Далее мы разберем, как найти эти координаты, если прямая у нас задана не в плоскости, а в пространстве.~~

~~Вектор a → = ( a x , a y , a z ) является направляющим для прямой, выраженной с помощью:~~

~~1) канонического уравнения прямой в пространстве x — x 1 a x = y — y 1 a y = z — z 1 a z~~

~~2) параметрического уравнения прямой в пространстве x — x 1 a x = y — y 1 a y = z — z 1 a z~~

Таким образом, для вычисления координат направляющего вектора нужно взять числа из знаменателей или коэффициентов при параметре в соответствующем уравнении.

~~Рассмотрим конкретную задачу.~~

Прямая в пространстве задана уравнением вида x — 1 4 = y + 1 2 0 = z — 3 . Укажите, какие координаты будет иметь направляющий вектор данной прямой.

~~Решение~~

В каноническом уравнении необходимые числа видны сразу в знаменателях. Получается, что ответом будет вектор с координатами 4 , 0 , — 3 . Координаты всех направляющих векторов данной прямой можно записать в виде 4 · t , 0 , — 3 · t при условии, что t является действительным числом.

~~Ответ: 4 · t , 0 , — 3 · t , t ∈ R , t ≠ 0~~

Вычислите координаты любого направляющего вектора для прямой, которая задана в пространстве с помощью параметрического уравнения x = 2 y = 1 + 2 · λ z = — 4 — λ .

~~Решение~~

~~Перепишем данные уравнения в виде x = 2 + 0 · λ y = 1 + 2 · λ z = — 4 — 1 · λ .~~

~~Из этой записи можно вычленить координаты нужного нам вектора – ими будут коэффициенты перед параметром.~~

Разберем еще один случай. Как вычислить нужные координаты, если прямая задана уравнением двух пересекающихся плоскостей вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 ?

Есть два способа. Можно записать это уравнение в параметрическом виде, где будут видны нужные координаты. Но можно использовать и другой способ. Объясним его.

Вспомним, что такой нормальный вектор плоскости. Он по определению будет лежать на прямой, перпендикулярной исходной плоскости. Значит, любой направляющий вектор прямой, которая в ней находится, будет перпендикулярен ее любому нормальному вектору.

Направляющий вектор прямой, образованной пересечением двух плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , будет перпендикулярен нормальным векторам n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) . То есть в качестве направляющего вектора мы может взять произведение векторов n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) .

n 1 → × n 2 → = i → j → k → A 1 B 1 C 1 A 2 B 2 C 2 — это и есть направляющий вектор прямой, по которой пересекаются исходные плоскости.

~~Решим задачу, в которой применяется этот подход.~~

Запишите координаты направляющего вектора прямой, выраженной с помощью уравнения x + 2 y + 3 z — 1 = 0 2 x + 4 y — 4 z + 5 = 0 .

~~Решение~~

Возьмем произведение двух нормальных векторов плоскостей x + 2 y + 3 z — 1 = 0 и 2 x + 4 y — 4 z + 5 = 0 . У них следующие координаты: 1 , 2 , 3 и 2 , 4 , — 4 .

~~У нас получится:~~

n 1 → × n 2 → = i → j → k → 1 2 3 2 4 — 4 = i → · 2 · ( — 4 ) + j → · 3 · 2 + k → · 1 · 4 — — k → · 2 · 2 — i → · 3 · 4 — j → · 1 · ( — 4 ) = — 20 · i → + 10 · j → + 0 · k →

Выходит, что вектор n 1 → × n 2 → = — 20 · i → + 10 · j → + 0 · k → ⇔ n 1 → × n 2 → = — 20 , 10 , 0 – это и есть нужный нам направляющий вектор прямой.

Ответ: — 20 , 10 , 0

В конце статьи отметим, что умение вычислять направляющий вектор пригодится для решения многих задач, таких, как сопоставление двух прямых, доказательство их параллельности и перпендикулярности, вычисление угла между пересекающимися или скрещивающимися прямыми и др.