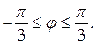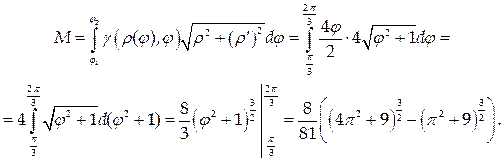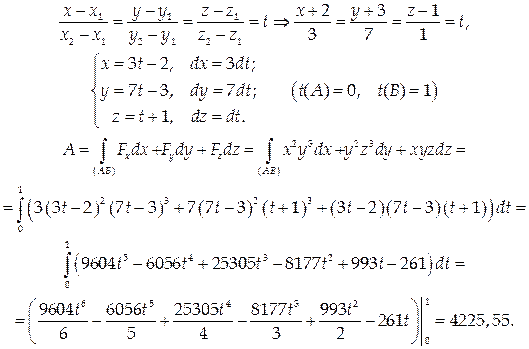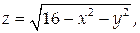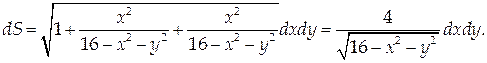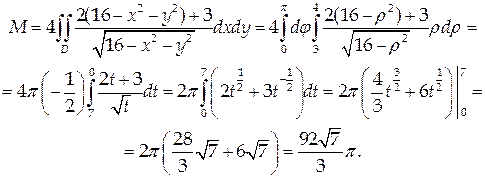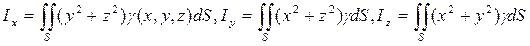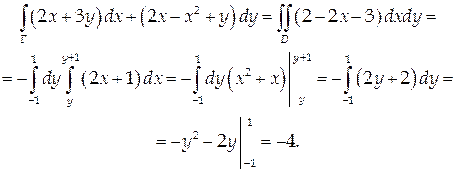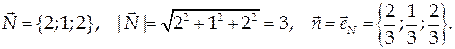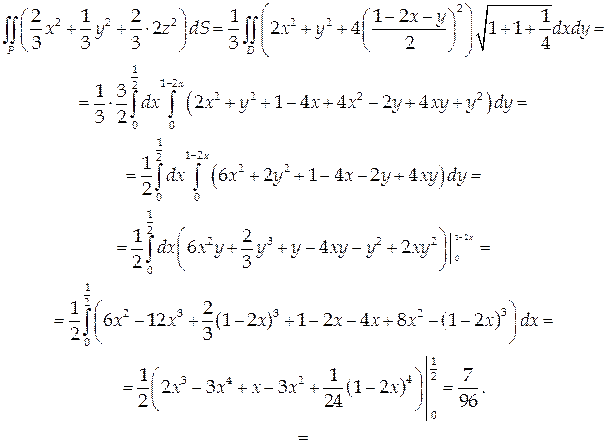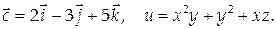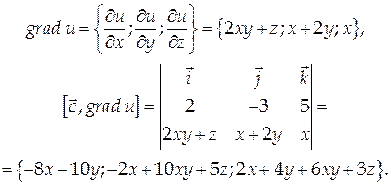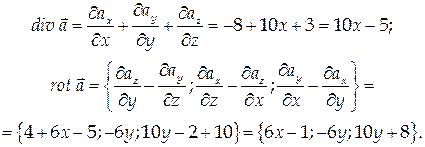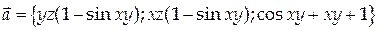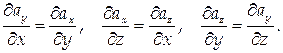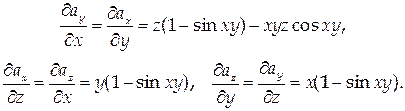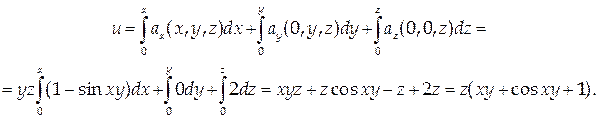Вариант 1     Вариант 2     Вариант 3     Вариант 4     Вариант 5     Вариант 6
        Вариант 7     Вариант 8     Вариант 9     Вариант 10     Вариант 11     Вариант 12
    Вариант 13     Вариант 14     Вариант 15     Вариант 16     Вариант 17     Вариант 18
    Вариант 19     Вариант 20     Вариант 21     Вариант 22     Вариант 23     Вариант 24
    Вариант 25     Вариант 26     Вариант 27     Вариант 28     Вариант 29     Вариант 30
        19.4 Вычислить длину дуги кривой, заданной уравнением в полярных координатах 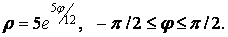
Видео:Построение кривой в полярной системе координатСкачать

Криволинейные интегралы
Криволинейный интеграл 1-го рода
Если подынтегральная функция f(x, y, z) ? 1, то из определения криволинейного интеграла 1-го рода получаем, что в этом случае он равен длине кривой, по которой ведется интегрирование:
Считая, что подынтегральная функция ? (x, y, z) определяет плотность каждой точки кривой, найдем массу кривой по формуле
Найти массу кривой с линейной плотностью , заданной в полярных координатах уравнением
Используем формулу (86):
3. Моменты кривой l найдем, рассуждая так же, как в случае плоской области:
— статические моменты плоской кривой l относительно осей Ох и Оу;
- — (88)
- — момент инерции пространственной кривой относительно начала координат;
- -моменты инерции кривой относительно координатных осей.
- 4. Координаты центра масс кривой вычисляются по формулам
Криволинейный интеграл 2-го рода
Если считать, что сила действует на точку, движущуюся по кривой (АВ), то работа этой силы может быть представлена как
то есть криволинейным интегралом 2-го рода.
Вычислить работу силы , действующей на точку, движущуюся по прямой от точки А(2; 1; 0) до точки В(-3; 2; 1).
Параметрические уравнения прямой АВ имеют вид:
При этом dx = -5dt, dy = dt, dz = dt.
- 4. Поверхностный интеграл 1-го рода
- 1. Площадь криволинейной поверхности, уравнение которой
z = f(x, y), можно найти в виде:
- (? — проекция S на плоскость Оху).
- 2. Масса поверхности
Найти массу поверхности S: x2 + y2 + z2 = 4, с поверхностной плотностью .
Зададим поверхность S в явном виде: и найдем dS:
Поверхность S представляет собой часть сферы радиуса 2 с центром в начале координат, вырезанную плоскостью . Найдем проекцию этой поверхности на координатную плоскость Оху. Линией пересечения сферы и плоскости является окружность , то есть х2 + у2 = 1. Следовательно, проекцией S на плоскость Оху является круг единичного радиуса с центром в начале координат.
Вычислим массу поверхности в полярных координатах:
— статические моменты поверхности относительно координатных плоскостей Oxy, Oxz, Oyz;
— моменты инерции поверхности относительно координатных осей;
— моменты инерции поверхности относительно координатных плоскостей;
- — момент инерции поверхности относительно начала координат.
- 4. Координаты центра масс поверхности:
Замечание. Так как формулы, задающие значения геометрических и физических величин с помощью интегралов, выводятся с помощью одних и тех же приемов для интегралов всех рассматриваемых типов, подробный их вывод дается только в начале главы. При желании можно провести аналогичные рассуждения для тройных, криволинейных и поверхностных интегралов и получить все формулы, приводимые без подробного вывода.
Видео:Площадь фигуры, заданной в полярной системе координатСкачать

Геометрические и физические приложения
Если подынтегральная функция f(x, y, z) ≡ 1, то из определения криволинейного интеграла 1-го рода получаем, что в этом случае он равен длине кривой, по которой ведется интегрирование:
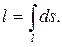
Считая, что подынтегральная функция γ (x, y, z) определяет плотность каждой точки кривой, найдем массу кривой по формуле
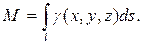
Пример 6.
Найти массу кривой с линейной плотностью 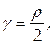
Используем формулу (40) с учетом того, что кривая задана в полярных координатах:
3) Моменты кривой l:
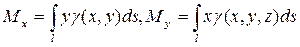
— статические моменты плоской кривой l относительно осей Ох и Оу;
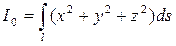
— момент инерции пространственной кривой относительно начала координат;
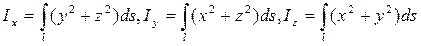
— моменты инерции кривой относительно координатных осей.
4) Координаты центра масс кривой вычисляются по формулам
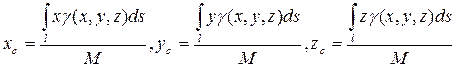
5) Работа силы 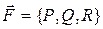
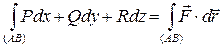
Пример 7.
Вычислить работу векторного поля 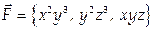
Найдем канонические и параметрические уравнения прямой АВ:
6) Площадь криволинейной поверхности, уравнение которой
z = f(x, y), можно найти в виде:
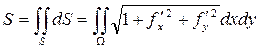
(Ω – проекция S на плоскость Оху).
7) Масса поверхности
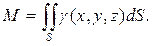
Пример 8.
Найти массу поверхности 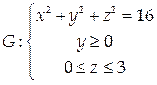
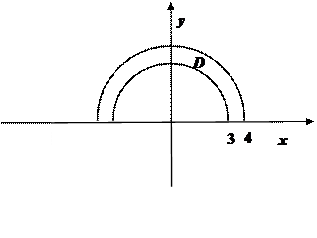
На рассматриваемой поверхности
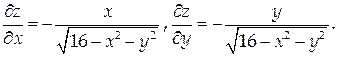
Проекцией D этой поверхности на координатную плоскость Оху является полукольцо с границами в виде дуг концентрических окружностей радиусов 3 и 4.
Применяя формулу (47) и переходя к полярным координатам, получим:
8) Моменты поверхности:
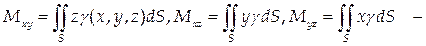
— моменты инерции поверхности относительно координатных осей;
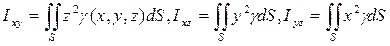
— моменты инерции поверхности относительно координатных плоскостей;
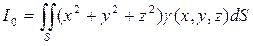
— момент инерции поверхности относительно начала координат.
9) Координаты центра масс поверхности:
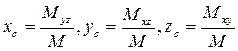
III. Теория поля
Если в каждой точке М определенной пространственной области задано значение некоторой скалярной или векторной величины, то говорят, что задано поле этой величины (соответственно скалярноеили векторное).
Если в некоторой области задано скалярное поле U(x,y,z), то вектор
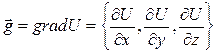
называется градиентомвеличины U в соответствующей точке.
Пусть дано векторное поле 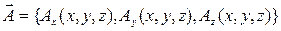
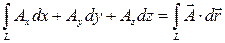
называется линейным интегралом от вектора 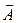
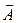
Пример 9.
Вычислить циркуляцию векторного поля 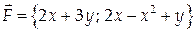
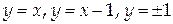
Воспользуемся формулой Грина:
Ротором или вектором вихрявекторного поля A = <Ax, Ay, Az>, где Ax, Ay, Az – функции от x, y, z, называется вектор, определяемый следующим образом:
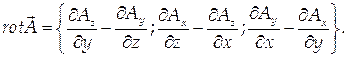
Рассмотрим векторное поле А(М), определенное в пространственной области G, ориентированную гладкую поверхность S 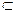
Поверхностный интеграл 1-го рода
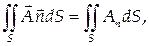
где An – скалярное произведение соответствующих векторов, а Ап – проекция вектора А на направление нормали, называется потоком векторного поля А(М) через выбранную сторону поверхности S.
Пример 10.
Найти поток векторного поля 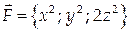
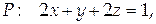
Проекцией данной поверхности на координатную плоскость Оху является треугольник с вершинами в точках А(0;0), В(0;1), С(½; 0). Найдем координаты единичной нормали к плоскости:
Вычислим соответствующий поверхностный интеграл (формула (56)):
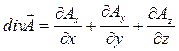
Пример 11.
Найти дивергенцию и ротор векторного поля 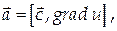
Найдем координаты вектора а:
Векторное поле A = <Ax, Ay, Az> называется потенциальным, если вектор А является градиентом некоторой скалярной функции u = u(x, y, z):
A = grad u = 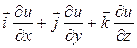
При этом функция и называется потенциалом данного векторного поля.
Пример 12.
Проверить, является ли векторное поле
потенциальным, и в случае положительного ответа найти потенциал и, считая, что в начале координат он равен нулю.
Поле является потенциальным, если выполнены следующие условия:
Следовательно, поле 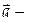
Векторное поле A = <Ax, Ay, Az> называется соленоидальным в области D, если в каждой точке этой области
🔍 Видео
Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Глаза гипножабы и площадь фигур в полярной системе координатСкачать

Площадь фигуры через двойной интеграл в полярных координатахСкачать

Полярная система координат.Скачать

1703 Вычисление длины линии в полярной системе координатСкачать

Полярная система координатСкачать

Двойной интеграл в полярных координатахСкачать

Длина дуги кривой| Урок 1| Надежда Павловна МедведеваСкачать

Тройной итеграл. Найти массу тела. Цилиндрическая СКСкачать

Масса через двойной интегралСкачать

Нахождение длины дуги кривойСкачать

Масса дугиСкачать

Математика без Ху!ни. Определенные интегралы, часть 3. Площадь фигуры.Скачать

Астроида: найдем площадь и длину через определенный интегралСкачать

Замена переменных в двойном интеграле. Полярные координаты. Пример 1.Скачать

Математический анализ, 47 урок, Криволинейные интегралы первого родаСкачать

Площадь пересечения эллипсов и двойной интеграл в полярной системе координатСкачать

Двойной интеграл: Полярная система координат | Решение задач 1.4 | ИнтФНПСкачать