С помощю этого онлайн калькулятора можно найти расстояние от точки до заданной плоскости. Дается подробное решение с пояснениями. Для вычисления расстояния от точки до плоскости введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».
- Предупреждение
- Расстояние от точки до плоскости − теория, примеры и решения
- Онлайн калькулятор. Расстояние от точки до плоскости
- Найти расстояние от точки до плоскости
- Ввод данных в калькулятор для вычисления расстояния от точки до плоскости
- Дополнительные возможности калькулятора для вычисления расстояния от точки до плоскости
- Теория: Расстояние от точки до плоскости
- Решение задач по математике онлайн
- Калькулятор онлайн. Вычисление расстояния от точки до плоскости
- 🎥 Видео
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:7 класс, 38 урок, Расстояние от точки до прямой. Расстояние между параллельными прямымиСкачать

Расстояние от точки до плоскости − теория, примеры и решения
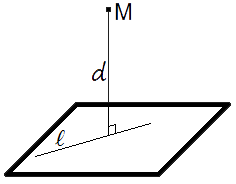
Для нахождения расстояния от точки M0 до плоскости α, необходимо найти расстояние от точки M0 до проекции точки M0 на плоскость α:
Нахождение расстояния от точки до плоскости содержит следующие шаги:
- построение прямой L, проходящей через точку M0 и перпендикулярной плоскости α.
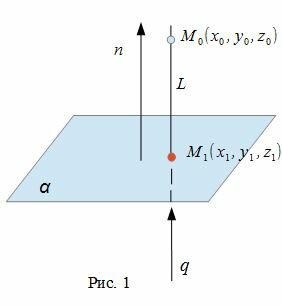
- нахождение точки M1 пересечения плоскости α с прямой L(Рис.1).
- вычисление расстояния между точками M0 и M1.
 |
1. Общее уравнение плоскости имеет вид:
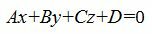 | (1) |
где n(A,B,C)− называется нормальным вектором плоскости.
Уравнение прямой, проходящей через точку M0(x0, y0, z0) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:
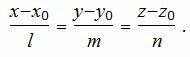 | (2) |
Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .
Таким образом, уравнение прямой, проходящей через точку M0(x0, y0, z0) и ортогональной плоскости (1) имеет следующий вид:
 | (3) |
Для нахождения точку пересечения прямой L с плоскостью α, проще всего рассматривать параметрическое уравнение прямой. Составим ее
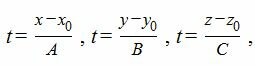 |
Выразим переменные x, y, z через рараметр t.
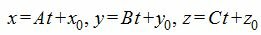 | (4) |
2. Найдем точку пересечения прямой (4) с плоскостью (1). Для этого нужно найти такой параметр t, при котором точка M(x, y, z) принадлежит плоскости (1). Поэтому подставим значения x,y,z из выражения (4) в (1) и решим относительно t.
| A(At+x0)+B(Bt+y0)+C(At+z0)+D=0, |
| A 2 t+Ax0+B 2 t+By0+C 2 t+Cz0+D=0, |
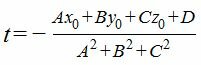 | (5) |
3. Найдем, наконец, расстояние от точки M0 до плоскости (1). Очевидно, что расстояние от точки M0 до плоскости (1) − это расстояние от точки M0 до точки M1. А это расстояние вычисляется так:
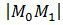 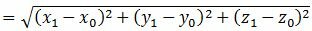 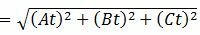 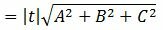 |
Учитывая значение параметра t, имеем:
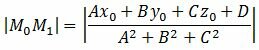  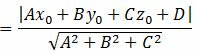 | (6) |
Пример 1. Найти расстояние от точки M0(2, -1, -9/31) до плоскости
 | (7) |
Нормальный вектор плоскости имеет вид:
Подставляя координаты точки M0 и нормального вектора плоскости в (5), получим:
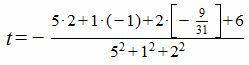 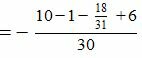  | (8) |
Из выражений (4) находим:
 |
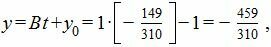 |
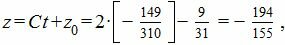 |
Проекцией точки M0(2, -1, -9/31) на плоскость (7) является точка:
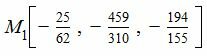 . . |
Вычислим расстояние между точками M0 и M1:
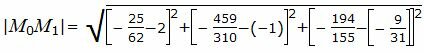 . . |
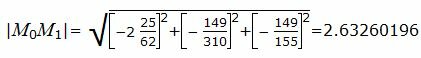 . . |
Расстояние от точки M0(2, -1, -9/31) до плоскости (7):
Видео:Задача C2: расстояние от точки до плоскостиСкачать

Онлайн калькулятор. Расстояние от точки до плоскости
Предлагаю вам воспользоваться онлайн калькулятором для вычисления расстояния от точки до плоскости.
Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление расстояния от точки до плоскости и закрепить пройденный материал.
Видео:Определение кратчайшей расстоянии от точки до плоскостиСкачать

Найти расстояние от точки до плоскости
Ввод данных в калькулятор для вычисления расстояния от точки до плоскости
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора для вычисления расстояния от точки до плоскости
- Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.
Теория: Расстояние от точки до плоскости
Расстояние от точки до плоскости — равно длине перпендикуляра, опущенного из точки на плоскость.
Если задано уравнение плоскости A x + B y + C z + D = 0, то расстояние от точки M(M x , M y , M z ) до плоскости можно найти используя следующую формулу
| d = | |A·M x + B·M y + C·M z + D| |
| √ A 2 + B 2 + C 2 |
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:Взаимно перпендикулярные плоскости. Определение кратчайшей расстоянии от точки до прямойСкачать

Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Видео:10 класс, 19 урок, Расстояние от точки до плоскостиСкачать

Калькулятор онлайн.
Вычисление расстояния от точки до плоскости
Этот калькулятор онлайн вычисляет расстояния от точки до плоскости заданной в виде общего уравнения плоскости:
$$ Ax+By+Cz+D=0 $$
Онлайн калькулятор для вычисления расстояния от точки до плоскости не просто даёт ответ задачи, он приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Наш онлайн калькулятор дает не только ответ задачи, но и отображает процесс решения по шагам. В результате вы сможете понять процесс решения задач на нахождение расстояния от точки до плоскости.
Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: ( -frac )
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: ( -1frac )
🎥 Видео
Расстояние от точки до различных поверхностейСкачать

Определение кратчайшей расстояние от точки до плоскости способом замены плоскостей проекцииСкачать

7. Расстояние от точки до плоскости (вывод формулы примеры)Скачать

расстояние от точки до плоскостиСкачать

Урок 10. Расстояние от точки до плоскости. Компенсация расстояний. Стереометрия с нуля.Скачать

✓ Как решать стереометрию | ЕГЭ-2023. Математика. Профильный уровень. Задание 13 | Борис ТрушинСкачать

Задача 7. Найти расстояние от точки M0 до плоскости, проходящей через три точки M1, M2, M3.Скачать

Перпендикуляр и наклонная в пространстве. 10 класс.Скачать

Теорема о трех перпендикулярах. Признак перпендикулярности плоскостей | Математика | TutorOnlineСкачать

Расстояние от точки до плоскости / Вывод формулыСкачать

Расстояние от точки до прямойСкачать

Расстояние от точки до плоскости.Метод ОбъемовСкачать

Замена плоскостей проекции(Расстояние от точки до прямой)Скачать

Лекция 24. Расстояние от точки до прямой на плоскости.Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать