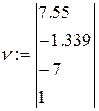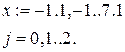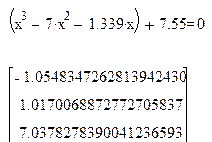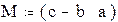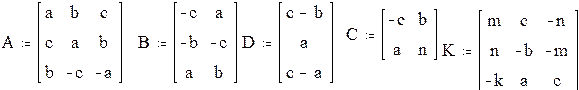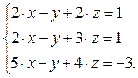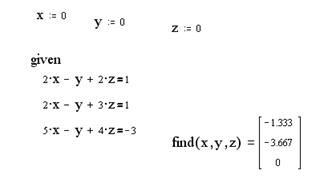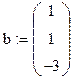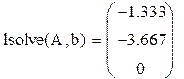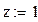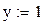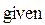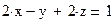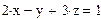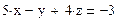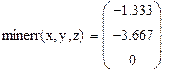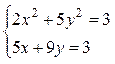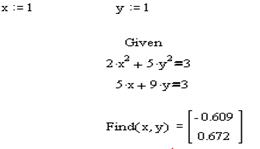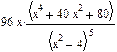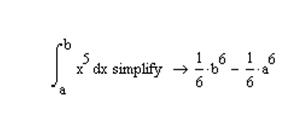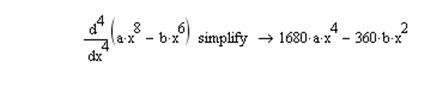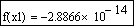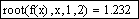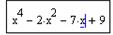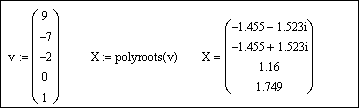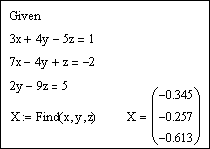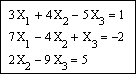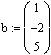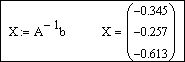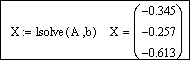Численное решение уравнений в MathCAD
Все задачи, с которыми вам приходилось сталкиваться в школе или изучать в университете, решались символьно. То есть вы тем или иным образом преобразовывали и упрощали выражения, использовали какие-то стандартные формулы и методы, умножали, делили, сокращали — и в результате приходили к какому-то аналитически несложному результату. Так, например, при решении квадратного уравнения вы использовали формулы Виета; пытаясь найти корни кубического уравнения, вы разлагали выражение на линейные множители (или, в крайнем случае, использовали формулу Кардано), для бикубических уравнений прибегали к замене. В общем, для того, чтобы решить даже очень несложное нелинейное уравнение, от вас требовалось знание великого множества разнообразных формул и подходов. Но, увы, как бы вы хорошо ни ориентировались во всех этих методах и подходах, зачастую это мало вам помогало, так как использование большинства из них крайне трудоемко и подходит для решения очень немногих (специально подобранных) уравнений. На практике же, как правило, приходится работать с уравнениями, включающими разнородные функции (что, как правило, автоматически означает невозможность символьного решения) или с очень неудобными коэффициентами. Справиться со многими из них привычным преобразованием или заменами никак не получится. Что же делать?
Естественно, если вам попадется такое «нерешаемое» уравнение, вы попытаетесь просто подобрать корни. Для этого вы будете подставлять какие-то значения переменной (выбор которых, скорее всего, в основном будет определяться вашей интуицией) в надежде на то, что какое-то из них обратит уравнение в нуль. К сожалению, и такой способ весьма малоэффективен на практике: подставив десяток-другой значений, вы почти наверняка предпочтете удовлетвориться мыслью о том, что данное уравнение не имеет решений вовсе, чем продолжать эту чрезвычайно неинтересную работу.
Но если у вас есть компьютер с системой MathCAD, то никаких проблем с поиском решения не будет вне зависимости от сложности уравнения. Конечно, аналитическое решение компьютер вряд ли найдет даже для очень простых уравнений (в этом пока человек значительно превосходит машину), но зато ввиду колоссальной по сравнению с человеческой скоростью обработки данных очень эффективными становятся так называемые численные методы.
В основе всех численных методов решения уравнений лежит принцип подбора. Но, в отличие от подбора возможных корней человеком, в численных методах этот процесс является строго направленным. Основным понятием численных методов является итерация. Итерация — это буквально повторение, то есть все численные методы построены на принципе повторения одного и того же действия или последовательности действий, результатом которых является большее или меньшее приближение некоторого рабочего значения переменной к корню. Поэтому численные методы решения уравнений называются еще итерационными. Число необходимых итераций определяется скоростью сходимости алгоритма (эффективностью). Эффективность различных численных алгоритмов может различаться весьма значительно, но это не значит, что всегда стоит избирать из них наиболее быстрый: чем выше скорость сходимости к решению, тем, как правило, чувствительность алгоритма к различного рода трудностям (многочисленным экстремумам, разрывам или недифференцируемости в некоторых точках) выше. Поэтому очень важно иметь представление (хотя бы самое поверхностное) о том, какие принципы лежат в основе работы той или иной функции: это поможет выбрать наиболее подходящий в рамках данной задачи алгоритм и тем самым избежать лишних ошибок и проблем.
Немного о выборе типа алгоритма. В общем случае, конечно, гораздо лучше получить решение в результате символьных преобразований, так как при этом можно найти сразу все корни (при использовании встроенных функций MathCAD — только один), причем без какой-либо погрешности. Но, увы, аналитическое решение имеет относительно небольшое количество задач, а символьный процессор MathCAD сможет справиться вообще с мизерным процентом уравнений. Так что применение численных методов — это печальная необходимость. Но особо огорчаться по этому поводу не стоит: все недостатки численных алгоритмов MathCAD можно легко преодолеть.
Для численного поиска решений алгебраических уравнений с одним неизвестным в MathCAD существует специальная встроенная функция root (корень). Функция эта может использоваться с различными начальными условиями, при этом реализуются разные численные алгоритмы. Так, если определена только одна точка приближения к корню, поиск решений будет осуществляться так называемым методом секущих. Если же задан интервал, на котором предположительно локализовано решение, то поиск его будет осуществлен с применением метода деления пополам (или метода Больцано).
Если необходимо найти корень некоторого уравнения, причем известен интервал, в котором находится корень, проще всего использовать функцию root с 4 аргументами: root(f(x), x, a, b), где f ( x ) — функция, определяющая уравнение, x — переменная, a и b — границы интервала локализации. Обязательным условием является то, что значения функции на концах интервала должны быть противоположных знаков.
Попробуем протестировать функцию root и для этого найдем корни какого-нибудь уравнения, точное решение которого очевидно. К примеру, возьмем уравнение
все корни которого имеют вид p × N/4 (N=1, 2, . ). Попробуем найти первое положительное решение. Очевидно, что таковым будет x=p /4 (что очень хорошо видно на графике).
Посмотрим, однако, найдет ли этот корень функция root. Интервал локализации определим от 0 до p /3:
MathCAD не подвел на этот раз: решение найдено в точности. Попробуем решить это уравнение с другим интервалом локализации:
Полученный результат отличается от первого решения, хотя корень х =0.25 (находится в данном интервале. Все дело в том, что в этом же промежутке находится еще 4 корня, и заранее предсказать, какой именно из них будет выдан в качестве ответа, совершенно невозможно. Поэтому следует ввести еще одно ограничение для применения функции root в рассматриваемой интерпретации: на промежутке должен быть локализован только один корень. В тех случаях, когда определить границы такой локализации невозможно, следует применять функцию root с одной точкой приближения (то есть перейти от метода Больцано к методу секущих). Хотя практически всегда определить нужный промежуток можно и чисто визуально, предварительно задав график. Вообще, строить график всегда желательно, когда вы используете численные методы: это самый надежный способ избежать ошибок и не потерять корни. Другой вопрос, что в случае систем уравнений это может помочь очень мало (так как сделать какие-то более или менее точные выводы по двум пересекающимся поверхностям совершенно невозможно).
Очень важной характеристикой решения является его точность. В MathCAD можно регулировать величину погрешности решения, изменяя значение специальной системной переменной TOL (от английского tolerance — точность). Строго говоря, TOL — это параметр, определяющий условие прекращения итераций. То есть цикл численного алгоритма остановит свою работу и выдаст последнее значение x, если f ( x ) примет значение, меньшее, чем TOL. Изменить величину этой встроенной переменной можно либо при помощи команды Math/Options/Built-in variables/TOL (Математические/Опции/Системные переменные/TOL), либо выполнив соответствующее присваивание непосредственно слева или сверху функции численного решения. Посмотрим, как влияет изменение величины TOL (по умолчанию равной 10 -3 ) на точность поиска корня. Пусть дана следующая функция:
Для того чтобы определить существование у нее нулей, а также, при их наличии, приблизительные границы интервала локализации корней, построим график:
Один корень вполне очевиден — это 0. Посмотрим, однако, сможет ли найти его функция root. Попробуем провести такой расчет при различных значениях TOL:
Для такой невысокой точности результат получился на удивление неплохим (значение функции в точке, определенной как корень, на 3 порядка меньше TOL — условия остановки цикла алгоритма). Но все равно 0.066 — это довольно далеко от настоящего значения корня. А то, что значение f ( x ) в этой точке весьма близко к нулю, совсем неудивительно: это связано с особенностью поведения функции в окрестности 0, где она буквально «скользит» по оси X .
При уменьшении TOL на три порядка приблизительно во столько же порядков увеличилась и точность решения (что вполне закономерно). Новое значение корня может удовлетворить большинству требований к точности, возникающих на практике. Но все же мы попытаемся получить максимально точное решение. Для этого еще более уменьшим значение TOL:
Значение корня уже крайне близко к нулю. Попробуем задать высшую точность, возможную в MathCAD (TOL=10 -15 ):
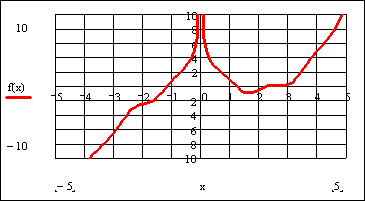
Только в этом предельном случае наконец удалось получить правильное решение. Проанализируем, с чем были связаны трудности в поиске нуля этой функции (как вы помните, решения для косинуса находились очень просто и без применения условия особой точности). Для этого построим график, на котором ясно видно прохождение кривой через точку корня. Сделать это проще всего можно при помощи инструмента ZOOM, который позволяет увеличивать отдельные фрагменты графика.
Более 30 раз пришлось повторить операцию с этим инструментом, пока наконец кривая перестала сливаться с осью X ! В результате получился следующий график:
Теперь совсем несложно понять причину возникших трудностей: просто кривая в окрестности 0 слишком близко подходит к оси X . А, как вы помните, корень считается найденным, когда значение функции в некоторой точке меньше TOL. В случае же рассматриваемой функции для стандартной точности (10 -3 ) такие точки появятся на относительно большом расстоянии от точки решения. Поэтому результат получается неверным. Но, с другой стороны, утверждать, что решение в рассмотренных выше случаях находилось ошибочное, совершенно некорректно. Ведь по условию в точке корня значение функции должно быть меньше TOL. Для большинства численных методов это основное, а в случае метода бисекции (схожий с ним алгоритм лежит в основе работы функции root с четырьмя аргументами) — единственное условие определения некоторой точки x как корня. Условие же это при всех значениях точности было выполнено, причем TOL и f ( x ) отличались на несколько порядков. Просто, строго говоря, получаемые значения корней следует округлять до порядка, равного порядку продекларированной точности (ведь значение функции не может быть точнее входных данных). Если бы мы это сделали, то во всех случаях, в том числе и при TOL=10 -1 , ответ получился бы верным (хотя, надо признать, в случае TOL=10 -1 это было бы, скорее, счастливое совпадение).
Из всего вышесказанного можно сделать вывод: нахождение корня функцией root совсем не означает его действительного существования. Очень даже возможна такая ситуация, когда кривая функции очень близко подходит к оси Х, но при этом не пересекает ее. Если же установленный уровень точности окажется больше того расстояния, на которое она приближается к оси, то точку, в которой это сближение происходит, MathCAD определит как корень.
Что же делать, чтобы избежать таких ошибок? Во-первых, всегда строить график. В системе MathCAD это делается предельно быстро и просто, а неприятностей позволяет избежать очень многих. Во-вторых, если вы видите, что график как бы скользит по оси Х (очень неясная ситуация: возможно и пересечение в 2-х точках, и касание в одной, и отсутствие общих точек вообще), попробуйте увеличить точность по максимуму: в большинстве случаев этого бывает вполне достаточно. И в-третьих, если сомнения все равно остаются, используйте инструмент ZOOM в области предполагаемого расположения корня. Пожалуй, способ этот самый надежный: ведь увеличение можно производить практически до бесконечности.
Найти решение уравнения в MathCAD можно применяя другую форму встроенной функции root, имеющую только 2 аргумента (имя функции и переменной). При использовании этого варианта выше или правее самой функции root следует задать начальное приближение для x:
Определить величину начального приближения можно либо чисто интуитивно, либо (лучше) построив график.
Вы можете задать резонный вопрос: если существует весьма верный и простой метод бисекции, зачем использовать другие, менее надежные (как будет показано далее) методы? Тут все дело вот в чем: во-первых, не всегда существованию корня сопутствует интервал с различными по знаку значениями функции в точках его границ (есть возможность простого касания); во-вторых, метод бисекции не очень удобно использовать при программном поиске всех корней уравнения сканированием некоторой широкой области; в-третьих, ввиду того, что построенные при помощи компьютерных программ графики отражают вид функции довольно искаженно, определение при их помощи интервала локализации корня нельзя считать абсолютно надежным.
Однако можно утверждать, что лучше воздержаться от использования метода секущих (то есть функции root в варианте с начальным приближением) в случае периодических функций (особенно сложного вида), очень осторожно следует применять ее при наличии локальных экстремумов (и ни в коем случае не определять начальное приближение вблизи таких точек, а также точек перегиба) и точек разрыва. Также следует учитывать поведение функции на бесконечности. Поэтому во всех сложных случаях куда лучше применять метод бисекции.
Дмитрий Гурский, Юрий Стрельченко, dot@omen.ru
Компьютерная газета. Статья была опубликована в номере 07 за 2003 год в рубрике soft :: текст
Видео:Числовое решение. Функция root в MathCAD 14 (28/34)Скачать

Нахождение корней уравнения в MathCad
Дата добавления: 2015-07-23 ; просмотров: 18071 ; Нарушение авторских прав
Цель работы:нахождение корней уравнения в программе MathCad с использованием встроенных функций root,polyroots, символьного решения.
Указания к выполнению лабораторной работы:
IНахождение корней уравнения в программе MathCad с использованием встроенной функции root
1. Запустить программу MathCad .
2. Записать на рабочем листе MathCad вид функции f(х), для которой необходимо найти на заданном интервале корни.
3. Создать цикл из точек интервала, на котором определяются корни, и вычислить в этих точках функцию f(х). Построить график функции f(х) и график функции х0=0 (т.е. ось х).
4. Определить точки пересечения двух кривых f(х) и х0, которые будут приближением к корням уравнения.
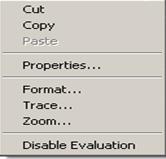
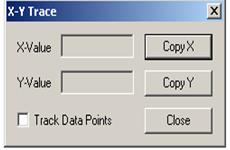
4.1. Использовать для определения на графике значений корней в контекстном меню (рис.17, a) опцию Trace (рис. 17,б), установить флажок в окне Track Data Poіnt.
4.2. Подвести курсор мыши к точкам пересечения кривых, координаты точек пересечения кривых, т.е. корни, будут представлены в окнах Х-Value и У- Value, а на графике отобразится вертикальная прямая.
5. Задать для независимой переменной х начальное приближение, которое выбирается как значение точки пересечения кривых f(х) и х0. Обратиться ко встроенной в MathCad функции root(f(x), x) (функция root возвращает значение независимой переменной х, для которой f(х) равняется 0) и найти корень х1.
6. Найти второй (х2) и третий (х3) корни уравнения f(х)=0 (уравнение третьей степени имеет не больше трех действительных корней), задав для них соответственно их начальные значения как координаты точек пересечения кривых f(х) и х0 и использовав функцию root.
Рисунок 17 – Диалоговые окна для определения координат точек пересечения кривых
ІІ Нахождение корней уравнения в программе MathCad с использованием встроенной функции polyroots, которая возвращает вектор, имеющий все корни уравнения, коэффициенты уравнения при этом задаются вектором.
1. Записать на рабочем листе MathCad вид функции f(х), для которой необходимо найти на заданном интервале корни.
2. Записать как вектор v все коэффициенты уравнения, расположить их в порядке увеличения степеней.
3. Найти корни, обратившись ко встроенной функции r:=polyroots(v), результат будет получено относительно трансформированного вектора r T .
4. Для интервала нахождения корня и количества элементов вектора r T создать соответствующие циклы и вычислить значение функции в точках цикла.
5. Построить график функции в точках цикла, а также в найденных точках корней, в которых функция будет иметь значения, равные нулю.
ІІІ Нахождение корней уравнения в программе MathCad с использованием символьных решений уравнений.
1. Ввести левую часть уравнения.
2. Ввести знак равенства с использованием панели управления Evaluatіon (Выражения) или с помощью нажатия клавиш Ctrl + =.
3. За знаком равенства ввести правую часть уравнения.
4. Выделить переменную, относительно которой решается уравнение.
5. Выбрать команду Symbolіc/Varіable/Solve.
По окончанию решения корни уравнения выводятся в виде вектора.
ІV Найти приближенное решение с использованием функции mіnerr(x1. ).
1. Задать приближение последовательно для первого корня х:=1.
2. Ввести ключевое слово gіven (дано), из которого начинается блок решений.
3. Записать уравнение, используя знак логического равенства между правой и левой частями уравнения.
4. Обратиться к функции mіnerr( x). Корень будет найдено.
Таблица 1.1 – Варианты заданий к лабораторной работе № 1
| № варианта | Интервал нахождения корней | Уравнение |
| [-1; 3] | x 3 -2,92x 2 +1,4355x+0,791=0 | |
| [-2; 3] | x 3 -2,56x 2 -1,325x+4,395=0 | |
| [-3,5; 2,5] | x 3 +2,84x 2 -5,606x-14,766=0 | |
| [-2,5; 2,5] | x 3 +1,41x 2 -5,472x-7,38=0 |
| [-1,6; 1,1] | x 3 +0,85x 2 -0,432x+0,044=0 |
| [-1,6; 1,6] | x 3 -0,12x 2 -1,478x+0,192=0 |
| [-1,6; 0,8] | x 3 +0,77x 2 -0,251x-0,017=0 |
| [-1,4; 1] | x 3 +0,88x 2 -0,3999x-0,0376=0 |
| [-1,4; 2,5] | x 3 +0,78x 2 -0,827x-0,1467=0 |
| [-2,6; 1,4] | x 3 +2,28x 2 -1,9347x-3,90757=0 |
| [-2,6; 3,2] | x 3 -0,805x 2 -7x+2,77=0 |
| [-3; 3] | x 3 -0,345x 2 -5,569x+3,15=0 |
| [-2; 3,4] | x 3 -3,335x 2 -1,679x+8,05=0 |
| [-1; 2,8] | x 3 -2,5x 2 +0,0099x+0,517=0 |
| [-1,2; 3] | x 3 -3x 2 +0,569x+1,599=0 |
| [-2,5; 2,5] | x 3 -2,2x 2 +0,82x+0,23=0 |
| [-1,2; 4,6] | x 3 -5x 2 +0,903x+6,77=0 |
| [-1; 7,4] | x 3 -7,5x 2 +0,499x+4,12=0 |
| [-1.6; 9] | x 3 -7,8x 2 +0,899x+8,1=0 |
| [-3,4; 2] | x 3 +2x 2 -4,9x-3,22=0 |
| [-3,4; 1,2] | x 3 +3x 2 -0,939x-1,801=0 |
| [-4,6; 3,0] | x 3 +5,3x 2 +0,6799x-13,17=0 |
| [-2,4; 8,2] | x 3 -6,2x 2 -12,999x+11,1=0 |
| [-3,2; 2,7] | x 3 -0,34x 2 -4,339x-0,09=0 |
| [-1; 3] | x 3 -1,5x 2 +0,129x+0,07=0 |
| [-1; 3] | x 3 -5,5x 2 +2,79x+0,11=0 |
| [-1; 3] | x 3 -5,7x 2 -6,219x-2,03=0 |
| [-1; 3] | x 3 -3,78x 2 -7,459x-4,13=0 |
| [-1; 3] | x 3 -5x 2 -9,9119x+0,01=0 |
| [-1; 3] | x 3 -7x 2 -1,339x-7,55=0 |
Пример
І Для уравнения 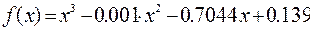
1 Записать цикл из точек интервала х:=-1, -0.9..1.
2 Записать функции 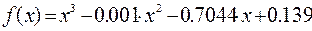
3 Построить графики для этих функций.
4 Определить на графике точки пересечения кривых 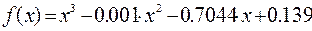
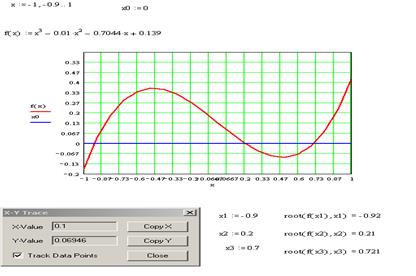
5 Задать как приближение значения точек пересечения х1, х2, х3. В примере х1=-0.9, х2=0.2, х3= 0.7.
6 Вычислить значение корней с помощью формул: root (f(x1),x1), root (f(x2),x2), root (f(x3),x3). Полученные значения корней такие: х1=-0.92, х2=0.21, х3= 0.721 (рис. 18).
Рисунок 18 – Результат нахождения корней с использованием функции root
II Для уравнения 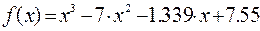
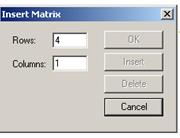
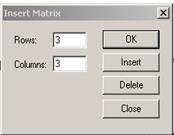
1. Создать вектор из коэффициентов уравнения, используя панель управления Matrix (Матрица) (рис.19) и задав один столбец и четыре строки для коэффициентов уравнения.
Рисунок 19 – Диалоговое окно для определения вектора из коэффициентов уравнения
Вектор из коэффициентов уравнения будет иметь следующий вид
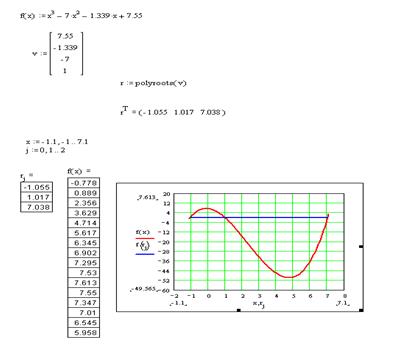
2. С помощью встроенной функции r:=polyroots(v) найти корни уравнения и представить их в виде вектора r T , транспонированного по отношению к r, то есть преобразованного из столбца в строку.
3. Создать циклы для переменной х и количества найденных корней:
4. Построить графики для функции и определить функцию в точках корней. В точках корней значения функции равны нулю.
5. Определить значения корней на графике (рис. 20).
Рисунок 20 – Результат нахождения корней с использованием функции polyroots
III Для уравнения 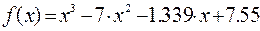
1. Записать левую часть уравнения
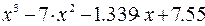
2. Поставить логический знак «=» и в правой части записать 0.
3. Выделить переменную х.
4. Обратиться в главном меню MathCad к команде Symbolic/Variable/ Solve.
Найдены корни уравнения запишутся в виде вектора:
IV Найти приближенное решение вышеприведенного уравнения с использованием функции minerr( x1,…).
1. Задать приближение последовательно для первого корня х:=1.
2. Ввести ключевое слово given (дано), с которого начинается блок решений.
3. Записать уравнение, используя знак логического равенства между правой и левой частью уравнения.
4. Обратиться к функции minerr( x). Корень будет найдено.
5. Аналогические действия выполнить для двух других корней уравнения, поскольку уравнения третьей степени имеет не больше трех корней.
Контрольные вопросы
1 Какие встроенные функции позволяют находить корни уравнения?
2 Как выполняется символьное нахождение корней уравнений?
Лабораторная работа №3
Действия с матрицами в MathCad
Цель работы:выполнение действий с матрицами в программе MathCad .
Указания к выполнению лабораторной работы:
1. Запустить программу MathCad .
2. Создать матрицы 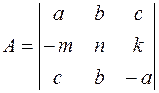
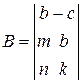
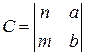
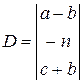
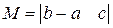
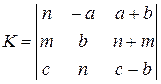
3. Выполнить действия с матрицами в соответствии с вариантом задания.
4. Найти ранг матрицы А.
5. В символьном виде выполнить транспонирование матрицы В, инвертирование матрицы А.
6. Найти обратную матрицу К. Найти детерминант матрицы А.
Таблица 2.1 – Варианты заданий к лабораторной работе № 2
| Номер варианта | Значение элементов матриц | Действия с матрицами |
| a=1; b=0.5; c=-1; m=2; k=-2.1;n=-0.8 | 1) A+A×M; 2) B×C; 3) M 3 ; 4)D+m×K; 5)A×D+D×M; 6)K -2 | |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 | |
| a=-1; b=5; c=1.3; m=0.9; k=0.1;n=-0.5 | 1) A-M; 2) B-a×C 3) M 2 -B; 4)D-×K; 5)A+7×D; 6)A -2 | |
| a=1; b=0.5; c=1; m=0.2; k=0.27 ;n=0.7 | 1) A 2 ; 2) B×C+M; 3) n×M 2 ; 4)D-K; 5)A×B-D×C; 6)D -2 | |
| a=3; b=2.1; c=0.91; m=1.2; k=1; n=3 | 1) A 2 +M; 2) B-M; 3) b×C -3 ; 4)D+3K; 5)A×K-D; 6)M -2 | |
| a=4; b=-0.5; c=-1; m=3.2; k=1.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 | |
| a=1; b=2.5; c=0.3; m=1; k=-2.1;n=-0.8 | 1) A-M; 2) B-a×C 3) M 2 -B; 4)D-×K; 5)A+7×D; 6)A -2 | |
| a=2; b=0.5; c=-1.1; m=2; k=1.9 ;n=-3.8 | 1) A 2 ; 2) B×C+M; 3) n×M 2 ; 4)D-K; 5)A×B-D×C; 6)D -2 | |
| a=3; b=-2.5; c=4; m=3; k=-2.1;n=0.8 | 1) A 2 +M; 2) B-M; 3) b×C -3 ; 4)D+3K; 5)A×K-D; 6)M -2 | |
| a=3.1; b=1.5; c=2.1; m=3.2; k=1.1;n=-1.6 | 1) A+A×M; 2) B×C; 3) M 3 ; 4)D+m×K; 5)A×D+D×M; 6)K -2 | |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 | |
| a=-1; b=5; c=1.3; m=0.9; k=0.1;n=-0.5 | 1) A-M; 2) B-a×C 3) M 2 -B; 4)D-×K; 5)A+7×D; 6)A -2 | |
| a=1; b=0.5; c=1; m=0.2; k=0.27 ;n=0.7 | 1) A 2 ; 2) B×C+M; 3) n×M 2 ; 4)D-K; 5)A×B-D×C; 6)D -2 | |
| a=3; b=2.1; c=0.91; m=1.2; k=1; n=3 | 1) A 2 +M; 2) B-M; 3) b×C -3 ; 4)D+3K; 5)A×K-D; 6)M -2 | |
| a=4; b=-0.5; c=-1; m=3.2; k=1.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 | |
| a=1; b=2.5; c=0.3; m=1; k=-2.1;n=-0.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 |
Продолжение табл. 2.1
| a=2; b=0.5; c=-1.1; m=2; k=1.9 ;n=-3.8 | 1) A-M; 2) B-a×C 3) M 2 -B; 4)D-×K; 5)A+7×D; 6)A -2 |
| a=3; b=-2.5; c=4; m=3; k=-2.1;n=0.8 | 1) A 2 ; 2) B×C+M; 3) n×M 2 ; 4)D-K; 5)A×B-D×C; 6)D -2 |
| a=3.1; b=1.5; c=2.1; m=3.2; k=1.1;n=-1.6 | 1) A 2 +M; 2) B-M; 3) b×C -3 ; 4)D+3K; 5)A×K-D; 6)M -2 |
| a=1; b=0.5; c=-1; m=2; k=-2.1;n=-0.8 | 1) A+A×M; 2) B×C; 3) M 3 ; 4)D+m×K; 5)A×D+D×M; 6)K -2 |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 |
| a=-1; b=5; c=1.3; m=0.9; k=0.1;n=-0.5 | 1) A-M; 2) B-a×C 3) M 2 -B; 4)D-×K; 5)A+7×D; 6)A -2 |
| a=1; b=0.5; c=1; m=0.2; k=0.27 ;n=0.7 | 1) A 2 ; 2) B×C+M; 3) n×M 2 ; 4)D-K; 5)A×B-D×C; 6)D -2 |
| a=3; b=2.1; c=0.91; m=1.2; k=1; n=3 | 1) A 2 +M; 2) B-M; 3) b×C -3 ; 4)D+3K; 5)A×K-D; 6)M -2 |
| a=4; b=-0.5; c=-1; m=3.2; k=1.1;n=1.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 |
| a=1; b=2.5; c=0.3; m=1; k=-2.1;n=-0.8 | 1) A+A×M; 2) B×C; 3) M 3 ; 4)D+m×K; 5)A×D+D×M; 6)K -2 |
| a=2; b=0.5; c=-1.1; m=2; k=1.9 ;n=-3.8 | 1) A+B×M; 2) M×C; 3) B 3 ; 4)C+m×K; 5)AB+D×K 6)D -3 |
| a=3; b=-2.5; c=4; m=3; k=-2.1;n=0.8 | 1) A-M; 2) B-a×C 3) M 2 -B; 4)D-×K; 5)A+7×D; 6)A -2 |
| a=3.1; b=1.5; c=2.1; m=3.2; k=1.1;n=-1.6 | 1) A 2 ; 2) B×C+M; 3) n×M 2 ; 4)D-K; 5)A×B-D×C; 6)D -2 |
| a=-2; b=1; c=1.5; m=-3; k=-0.1;n=1.8 | 1) A 2 +M; 2) B-M; 3) b×C -3 ; 4)D+3K; 5)A×K-D; 6)M -2 |
Пример
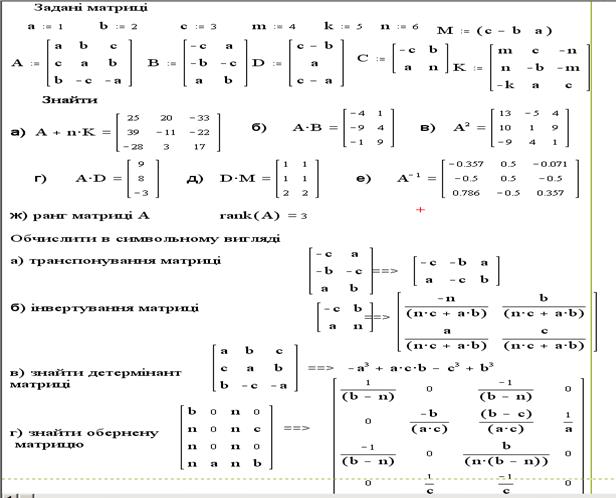
Выполнить действия с матрицами, создав их из заданных коэффициентов a=1, b=2, c= 3, m=4, k=5, n=6. Матрицы имеют следующий вид:
1. Создать матрицы.
1.1. Выбрать панель управления Matrіx (Матрица).
1.2. Определить число строк и столбцов для каждой матрицы (рис.21).
Рисунок 21 — Диалоговое окно для определения размера матрицы
1.3. Матрицы в примере имеют такие размеры: А — (3´3), В — (3´2), С(2´2), М(1´2), К(3´3).
1.4. Заполнить матрицы соответствующими параметрами (рис. 29).
2 Выполнить следующие действия с матрицами:
1) А+n·K; 2)A·B; 3) A 2 ; 4) A·D; 5)D·M; 6) D-1.
3 Найти ранг матрицы А (ранг матрицы -наибольший порядок минора этой матрицы, который отличный от нуля): rank(A).
4 В символьном виде выполнить транспонирование матрицы В, т.е. заменить местами строки и столбцы матрицы В.
4.1 Выделить матрицу В.
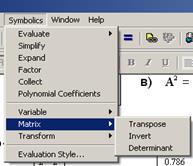
4.2 Обратиться в главном меню к команде Symbolіc / Matrіx/Transpose (рис. 28).
5 В символьном виде выполнить инвертирование матрицы А (т.е. найти матрицу, которая будет обратной к матрице А) .
5.1 Выделить матрицу A.
5.2 Обратиться в главном меню к команде Symbolіc/Matrіx/Іnvert (рис.28).
6 В символьном виде найти обратную матрицу К.
6.1 Выделить матрицу К.
6.2 Обратиться в главном меню к команде Symbolіc / Matrіx/Іnvert (рис.28).
7 В символьном виде найти детерминант (определитель) матрицы А.
7.1 Выделить матрицу A.
7.2 Обратиться в главном меню к команде Symbolіc/Matrіx/Determіnant (рис.22).
Рисунок 22 – Меню Symbolic для работы с матрицами в символьном виде
Рисунок 23 – Результаты вычисления матриц
Контрольные вопросы
1 Як можно создать матрицу и вектор?
2 Какие действия выполняются с матрицами?
3 Как определяются элементы матрицы?
Лабораторная работа №4
Нахождение решений системы линейных уравнений в MathCad
Цель работы:нахождение решений системы линейных уравнений в программе MathCad .
Указания к выполнению лабораторной работы:
I Найти решение системы линейных уравнений с использованием функции soln.
1 Запустить программу MathCad.
2 Создать матрицу А из коэффициентов при неизвестных.
3 Создать вектор b из свободных членов.
4 Обратиться к встроенной программе решения линейных уравнений soln и записать soln1:=А -1 ×b.
5 Получить решение линейного уравнения у векторному виде
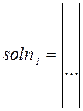
IIНайти решение системы линейных уравнений с использованием так званого «блоку решений».
1 Задать начальные значения переменным, которые есть в уравнении.
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать уравнение, используя знак логического равенства между правой и левой частью уравнения из панели управления Evaluation (Выражения).
4 Ввести ключевое слово find (найти), которым заканчивается блок решений.
IIIНайти решение вышеприведенной системы уравнений с использованием функции lsolve.
1Создать матрицу А из коэффициентов при неизвестных.
2 Создать вектор b из свободных членов.
4 Обратиться к встроенной программе решения линейных уравнений lsolve и записать lsolve(А,b).
5 Получить результат решения линейного уравнения в векторном виде
IVНайти приближенное решение с использованием функции minerr(x1,…).
1 Задать приближение последовательно для значений переменной х1, х2,… хn.
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать систему уравнений, используя знак логического равенства между правой и левой частями каждого уравнения.
4 Обратиться к функции minerr( x1,x2. ). Значения неизвестных будут найдены.
Таблица 3.1 – Варианты заданий к лабораторной работе № 3
| № варианта | Коэффициенты при неизвестных | Свободные члени | ||
| a11 а21 а31 а41 | а12 а22 а23 а24 | а13 а23 а33 а34 | а14 а24 а34 а44 | в1 в2 в3 в4 |
| 0,12 | -0,43 | 0,14 | 0,64 | -0,17 |
| -0,07 | 0,34 | -0,72 | 0,32 | 0,62 |
| 1,18 | -0,08 | -0,25 | 0,43 | 1,12 |
| 1,17 | 0,53 | -0,84 | -0,53 | 1,15 |
| 0,12 | -0,43 | 0,14 | 0,64 | -0,17 |
| -0,07 | 0,34 | -0,72 | 0,32 | 0,62 |
| 1,18 | -0,08 | -0,25 | 0,43 | 1,12 |
| 1,17 | 0,53 | -0,84 | -0,53 | 1,15 |
| 3,7 | 5,6 | 9,5 | ||
| 3,36 | 31,1 | 1,5 | ||
| 7,93 | 4,2 | 6,3 | 4,4 | |
| 42,7 | 3,7 | 6,2 | ||
| 1,3 | 1,6 | 2,2 | ||
| 4,4 | 6,7 | 2,5 | ||
| 2,8 | 0,73 | 67,8 | ||
| 3,4 | ||||
| 5,3 | 1,6 | 5,5 | 3,3 | |
| 4,1 | 6,4 | 3,9 | ||
| 2,1 | 3,3 | 2,04 | 4,9 | |
| 3,1 | ||||
| 0,2 | ||||
| 8,3 | 5,3 | |||
| 2,6 | 6,1 | 4,1 | ||
| 0,93 | 3,8 | |||
| 34,7 | ||||
| 3,6 | ||||
| 3,4 | 4,2 | |||
| 44,7 | ||||
| 5,1 | 0,2 | |||
| 3,4 | 5,34 | |||
| 2,7 | 6,7 | |||
| 3,3 | ||||
| 2,5 | 1,3 | |||
| 5,2 | 0,78 | |||
| 6,11 | 4,2 | |||
| 6,78 | 3,76 | |||
| 2,3 | ||||
| 3,4 | 2,5 | |||
| 0,2 | ||||
| 1,25 | ||||
| 3,3 | 8,2 | |||
| 1,2 | ||||
| 1,3 | ||||
| 5,9 | ||||
| 6,6 | ||||
| 3,3 | 2,1 | |||
| 4,8 | ||||
| 0,4 | ||||
| 0,2 | ||||
| 1,3 | 1,5 | 2,22 | 3,2 | |
| 3,4 | 5,55 | 1,3 | ||
| 3,3 | 2,2 | 6,77 | ||
| 4,9 | 3,6 | 6,88 | ||
| 0,4 | ||||
| 0,3 | ||||
| 3,3 | 7,6 | 5,5 | ||
| 5,4 | ||||
| 9,2 | ||||
| 3,2 | ||||
| 0,44 | ||||
| 0,67 |
| 3,35 | 5,3 | |||
| 4,22 | 6,7 | 3,5 | ||
| 2,8 | 3,8 | 2,9 | ||
| 2,34 | 3,44 | |||
| 5,23 | ||||
| 13,4 | 6,33 | 5,1 | 2,11 | 3,33 |
| 4,66 | 6,1 | 3,33 | 5,44 | 0,11 |
| 2,22 | 2,55 | 6,33 | 4,44 | |
| 2,98 | 3,78 | 6,11 | 3,33 |
Пример
I Найти решение системы уравнений с использованием функции soln
1 Создать матрицу А
А:= 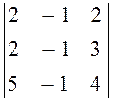
2 Создать вектор b
b:= 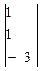
3 Найти решение системы, используя функцию soln
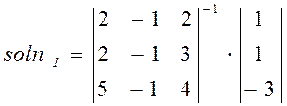
4 Результат решения
II Найти решение вышеприведенной системы уравнений с использованием так званого «блоку решений»
1 Задать начальные значения переменным, которые присутствуют в уравнении
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать уравнение, используя знак логического равенства между правой и левой частями уравнения из панели управления Evaluation (Выражения).
4 Ввести ключевое слово find (найти), которым заканчивается блок решений.
5 Результат решения
IIIНайти решение вышеприведенной системы уравнений с использованием функции lsolve.
1 Создать матрицу А
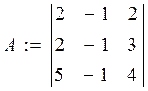
2 Создать вектор b
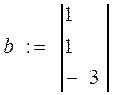
3 Найти решение системы, используя функцию lsolve:
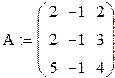
IVНайти решение вышеприведенной системы уравнений с использованием функции minerr (x,у,z).
1 Задать начальные условия для неизвестных, например, x=1,у=1,z=1.
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать уравнения, используя знак логического равенства между правой и левой частью уравнения из панели.
4 Обратиться к функции minerr (x,у,z). Решение системы уравнений будет найдено.
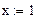
Контрольные вопросы
1 Какие встроенные функции позволяют найти решение системы линейных уравнений?
2 В каком виде представляются результаты решения системы линейных уравнений?
Лабораторная работа №5
Нахождение решений системы нелинейных уравнений в MathCad
Цель работы: нахождение решений системы нелинейных уравнений в программе MathCad .
Указания к выполнению лабораторной работы:
І Найти решение системы нелинейных уравнений с использованием так называемого «блока решений».
1 Задать начальные значения переменным, которые есть в уравнении.
2 Ввести ключевое слово gіven (дано), из которого начинается блок решений.
3 Записать уравнение, используя знак логического равенства между правой и левой частями уравнения из панели управления.
4 Ввести ключевое слово fіnd (найти), которым заканчивается блок решений.
ІІ. Найти приближенное решение с использованием функции mіnerr(x1. ).
1 Задать приближение последовательно для значений переменной х1, х2. хn.
2 Ввести ключевое слово gіven (дано), из которого начинается блок решений.
3 Записать систему уравнений, используя знак логического равенства между правой и левой частями каждого уравнения.
4 Обратиться к функции mіnerr( x1,x2. ). Значение неизвестных будет найдено.
Таблица 4.1 – Варианты задания к лабораторной работе №4
| № варианта | Система уравнений | № варианта | Система уравнений |
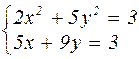 | 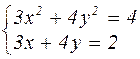 | ||
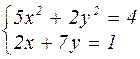 | 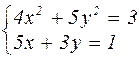 | ||
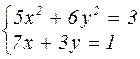 | 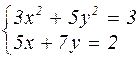 | ||
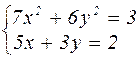 | 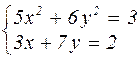 | ||
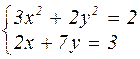 | 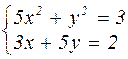 | ||
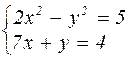 | 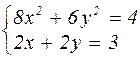 | ||
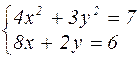 | 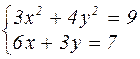 | ||
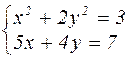 | 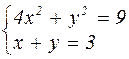 | ||
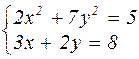 | 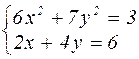 | ||
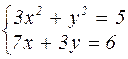 | 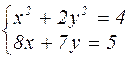 | ||
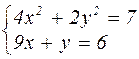 | 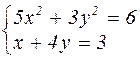 | ||
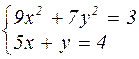 | 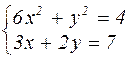 | ||
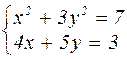 | 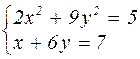 | ||
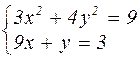 | 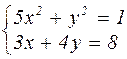 | ||
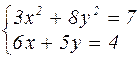 | 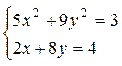 |
Пример
Найти решение системы нелинейных уравнений с использованием так называемого «блока решений».
1 Задать начальные значения переменным, которые есть в уравнении
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать уравнения, используя знак логического равенства между правой и левой частью уравнения из панели управления
4 Ввести ключевое слово find (найти), которым заканчивается блок решений.
5 Результат решения
IIНайти приближенное решение с использованием функции minerr(x1,…).
1 Задать приближения последовательно для значений переменной х=1, y=1.
2 Ввести ключевое слово given (дано), с которого начинается блок решений.
3 Записать систему уравнений, используя знак логического равенства между правой и лево частью каждого уравнения.
4 Обратится к функции minerr( x,y.). Значение неизвестных будет найдено.
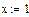 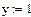 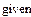 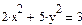 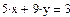 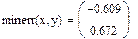 . . |
Контрольные вопросы
1 Какие встроенные функции позволяют найти решение системы нелинейных уравнений?
2 В каком виде представляются результаты решения системы нелинейных уравнений?
3 Нужно ли задавать начальные приближения при решении системы нелинейных уравнений?
Лабораторная работа № 6
Символьные действия математического анализа в MathCad
Цель работы:определение неопределенных и определенных интегралов и производных в программе MathCad с использованием символьных операций.
Указания к выполнению лабораторной работы:
1 Запустить программу MathCad.
2 Записать на рабочем листе в соответствии с номером варианта формулы для определения неопределенных интегралов, определенных интегралов, производных первого порядка. От производных первого порядка определить производные второго, третьего порядков.
3 Применить последовательно к каждой функции команды меню Symbolic/Simplify, отметив последовательно каждую из функций.
Таблица 5.1 – Варианты задания к лабораторной работе №5
| Номер варианта | Неопределенные интегралы | Определенные интегралы | Производные |
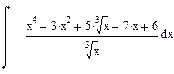 | 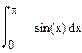 | 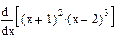 | |
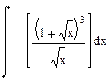 | 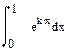 | 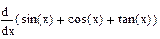 | |
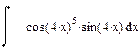 | 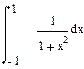 | 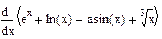 | |
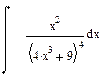 | 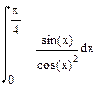 | 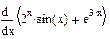 | |
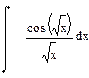 | 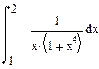 | 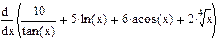 | |
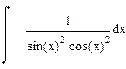 | 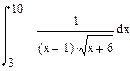 | 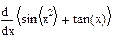 |
Продолжение табл. 5.1
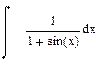 | 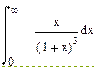 | 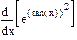 |
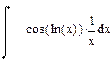 | 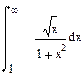 | 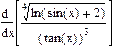 |
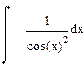 | 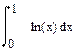 | 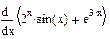 |
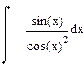 | 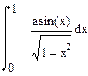 | 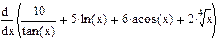 |
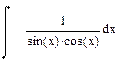 | 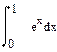 | 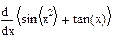 |
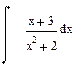 | 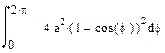 | 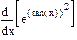 |
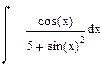 | 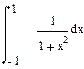 | 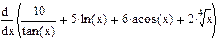 |
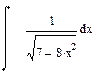 | 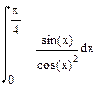 | 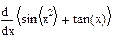 |
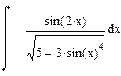 | 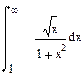 | 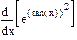 |
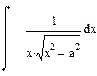 | 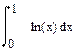 | 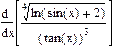 |
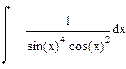 | 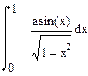 | 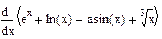 |
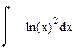 | 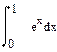 | 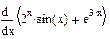 |
Продолжение табл. 5.1
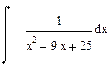 | 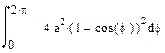 | 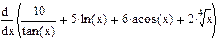 |
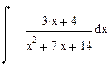 | 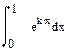 | 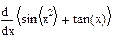 |
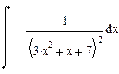 | 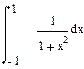 | 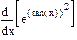 |
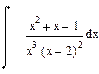 | 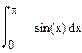 | 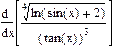 |
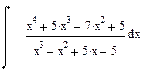 | 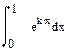 | 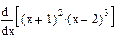 |
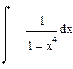 | 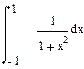 | 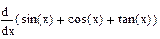 |
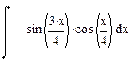 | 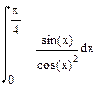 | 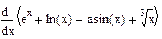 |
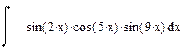 | 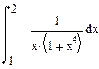 | 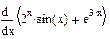 |
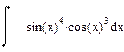 | 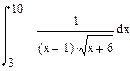 | 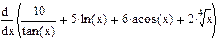 |
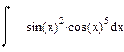 | 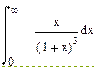 | 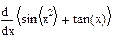 |
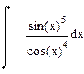 | 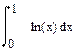 | 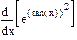 |
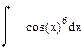 | 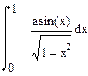 | 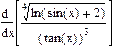 |
Примеры
1 Найти неопределенный интеграл 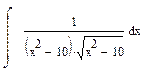
Результат 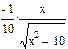
2 Найти определенный интеграл 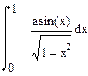
Результат 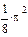
3 Найти производные первого порядка 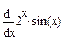
Результат 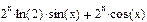
4 Найти производные высокого порядка 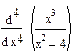
Результат
Контрольные вопросы
1 Как найти в символьном виде определенные и неопределенные интегралы?
2 Можно ли применять символьные операции к интегралам по области, к трехмерным интегралам, к контурным интегралам?
3 Можно ли в символьному виде найти производные высоких порядков?
| | | следующая лекция ==> | |
| Задание 3. | | | Лабораторная работа № 1 |
Не нашли то, что искали? Google вам в помощь!
Видео:Найти корень уравнения на заданном интервале (MathCad)Скачать

Найти корни уравнения численно mathcad
РЕШЕНИЕ УРАВНЕНИЙ И СИСТЕМ УРАВНЕНИЙ
4 Решение уравнений и систем средствами Mathcad
Система Mathcad обладает широкими возможностями численного решения уравнений и систем уравнений.
Функция root, блоки Given…Find, Given…Minerr
В ходе численного решения обычно выделяют два этапа:
- отделение корней – определение интервала нахождения каждого корня или определение приблизительного значения корня. В системе Mathcad наиболее наглядным будет отделение корней уравнения графическим способом;
- уточнение корней – нахождение численного значения корня с указанной точностью.
Точность нахождения корня устанавливается с помощью системной переменной TOL (Convergence Tolerance – Допуск сходимости), которая по умолчанию равна 10 -3 . Чем меньше значение TOL, тем точнее, вообще говоря, находится корень уравнения. Однако оптимальным является TOL = 10 -5 . Переопределить значение TOL можно в окне математических свойств документа Math Options на вкладке Build-In Variables (Встроенные переменные) или присваиванием, например, TOL:=0.0001.
Для решения одного уравнения с одной неизвестной предназначена встроенная функция root, которая в общем виде задается
root(f(x), x, [a, b])
и возвращает значение переменной x, при котором функция f(x) обращается в ноль. Аргументы функции root:
- f(x) – функция левой части уравнения f(x) = 0;
- x – переменная, относительно которой требуется решить уравнение;
- a, b (необязательные) – действительные числа, такие что a -1 слева: A -1 Ax=A -1 b. Учитывая, что A -1 A, вектор-столбец решений системы можно искать в виде
Этот прием используется в Mathcad так:
- задается матрица коэффициентов при неизвестных системы A;
- задается столбец свободных членов b;
- вводится формула для нахождения решения системы X:=A -1 b;
- выводится вектор решений системы X=.
Кроме того, пакет Mathcad имеет встроенную функцию
lsolve(A, b),
возвращающую вектор-столбец решений системы линейных алгебраических уравнений. Аргументами функции lsolve являются матрица коэффициентов при неизвестных системы и столбец свободных членов. Порядок решения аналогичен рассмотренному, но вместо формулы X:=A -1 b используется X:=lsolve(A, b).
Реализовать широко известный метод Гаусса решения систем линейных уравнений позволяет встроенная функция rref(M), возвращающая ступенчатый вид матрицы M. Если в качестве аргумента взять расширенную матрицу системы, то в результате применения rref получится матрица, на диагонали которой – единицы, а последний столбец представляет собой столбец решений системы.
Решение системы линейных уравнений можно осуществить с помощью блоков Given…Find, Given…Minerr. При этом неизвестным системы задается произвольное начальное приближение, а проверка необязательна.
Порядок выполнения лабораторной работы
- Загрузить Mathcad Start / All Programs / Mathsoft Apps / Mathcad (Пуск / Все программы / Mathsoft Apps / Mathcad).
- Сохранить в личной папке на диске z: новый документ с именем ФИО1, лучше использовать латинские буквы. Производить сохранение регулярно в процессе работы (Ctrl + S).
- Вставить текстовую область Insert / Text Region (Вставка / Область текста) и ввести в поле документа текст:
Лабораторная работа № 4
Решение уравнений и систем в Mathcad.
- В новой текстовой области ввести фамилию, имя, отчество, учебный шифр и номер варианта.
- Выполнить задание 1.
Задание 1. Решить уравнение 
Решение.
Решение данного уравнения будем проводить в два этапа: отделение корней уравнения графически, уточнение корней уравнения.
Определим функцию f(x), равную левой части данного уравнения, когда правая равна нулю:
Зададим ранжированную переменную x на некотором диапазоне с мелким шагом, например:
Вставим в документ графическую область. Для этого выберем дважды пиктограмму с изображением графика 
Снизу по оси абсцисс наберем x, а сбоку по оси ординат введем f(x).
Для появления графика щелкнем левой клавишей мыши вне графической области.
Отформатируем график функции f(x). Для этого щелкнем правой клавишей мыши в области графика и выберем в контекстном меню команду Format (Формат). Установим пересечение осей графика (Crossed – Только оси), добавим вспомогательные линии по координатным осям (Grid Lines – Вспомогательные линии). Отменим при этом автосетку (Autogrid – Автосетка) и установим количество линий сетки, равное 10.
Для подтверждения внесенных изменений нажмем последовательно кнопки Apply (Применить) и ОК.
После указанных преобразований график функции f(x) будет выглядеть следующим образом:
Из графика функции f(x) видно, что уравнение 
Этап отделения корней завершен.
Уточним теперь корни уравнения с помощью функции root.
Присвоим начальное приближение переменной x и укажем точность поиска корня:
Уточним заданное приближение к значению корня с помощью функции root:
Выполним проверку, подтверждающую, что первый корень найден с заявленной точностью:
Начальное приближение можно не задавать при использовании в качестве аргументов root границ отрезка нахождения корня, например, второй корень можно уточнить:
Задание 2. Решить уравнение 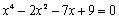
Решение.
Напечатаем левую часть уравнения, не приравнивая выражение к 0, и выделим синим курсором переменную x:
Выберем из главного меню Symbolics / Polynomial Coefficients (Символика / Коэффициенты полинома). Появившийся вектор коэффициентов полинома выделим целиком синим курсором и вырежем в буфер обмена, используя кнопку Вырезать 
Напечатаем v := и вставим вектор из буфера обмена, используя кнопку Вставить 
Для получения результата напечатаем polyroots(v) =:
Задание 3. Решить систему линейных уравнений 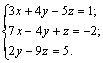
Решение.
1-й способ. Использование блока Given … Find.
Зададим всем неизвестным, входящим в систему уравнений, произвольные начальные приближения, например:
Напечатаем слово Given. Установим визир ниже и наберем уравнения системы, каждое в своем блоке. Используем при этом логический знак равенства (Ctrl + =).
После ввода уравнений системы напечатаем X := Find(x, y, z) и получим решение системы в виде вектора, состоящего из трех элементов:
Сделаем проверку, подставив полученные значения неизвестных в уравнения системы, например, следующим образом
После набора знака «=» в каждой строке должен быть получен результат, равный или приблизительно равный правой части системы. В данном примере системная переменная ORIGIN = 1.
2-й способ. Использование блока Given…Minerr.
Порядок решения системы этим способом аналогичен порядку использования блока Given … Find и представлен ниже вместе с проверкой:
3-й способ. Решение системы линейных уравнений матричным способом.
Создадим матрицу А, состоящую из коэффициентов при неизвестных системы. Для этого напечатаем A := , вызовем окно создания массивов (Ctrl + M). Число строк (Rows) и столбцов (Columns) матрицы данной системы равно 3. Заполним пустые места шаблона матрицы коэффициентами при неизвестных системы, как показано ниже:
Зададим вектор b свободных членов системы. Сначала напечатаем b :=, затем вставим шаблон матрицы(Ctrl + M), где количество строк (Rows) равно 3, а количество столбцов (Columns) равно 1. Заполним его:
Решим систему матричным способом по формуле
Решим систему с помощью функции lsolve:
Для проверки правильности решения системы, полученного матричным способом, достаточно вычислить произведение A·X, которое должно совпасть с вектором-столбцом свободных членов b:
🎦 Видео
Mathcad-09. Пример: уравненияСкачать

Числовое решение. Функция polyroots в MathCAD 14 (27/34)Скачать

MathCAD Поиск корней полиномаСкачать

Работа с MathCad Prime. Решение дифференциальных уравнений.Скачать

Mathcad Prime. Урок 5 - Способы решения уравненийСкачать

MathCAD Решение уравнений с помощью функции root 1 вариантСкачать

Приближенное решение систем уравнений в MathCAD 14 (30/34)Скачать

Ключевое слово solve в MathCAD 14 (26/34)Скачать

MathCAD. Given - FindСкачать

Полиномы. Численное нахождение корней полинома. Урок 36Скачать

3 Шаговый метод Mathcad Численные методы решения нелинейного уравненияСкачать

8. MathCad. Решение систем линейных алгебраических уравненийСкачать

7 Метод половинного деления Mathcad Численные методы решения нелинейного уравненияСкачать

11 Метод Ньютона (Метод касательных) Mathcad Численные методы решения нелинейного уравненияСкачать