Пример 1. Вычислить координаты вершин ромба, если известны уравнения двух его сторон: и и уравнение одной из его диагоналей: . Решение. Выясним взаимное расположение известных сторон ромба. Угловой коэффициент k прямой определяется по формуле:
Стороны параллельны, так как имеют одинаковый угловой коэффициент:
Для построения рисунка (рис. 4.1) запишем уравнения в отрезках для данных прямых:
Наметим план решения: 1) находим вершины ромба P и Q ; 2) находим точку пересечения диагоналей ромба N ; 3) через точку N проводим диагональ D 2 ; 4) находим оставшиеся вершины ромба R и S .1) Так как точка P является точкой пересечения прямых L 2 и D 1 , то ее координаты находим из системы уравнений:
Из рис. 4.1 сразу находим координаты точки Q (- 2, 0) . 2) Так как диагонали ромба в точке пересечения делятся пополам, то точка является серединой отрезка PQ , поэтому ее координаты — полусумма соответствующих координат точек P и Q :
3) Так как диагонали ромба взаимно перпендикулярны, то прямая D 2 перпендикулярна вектору . Найдем его координаты:
По формуле (3.1) находим уравнение диагонали D 2 как уравнение прямой, проходящей через точку N (- 3, 1) перпендикулярно вектору = :
2( x — (- 3)) + (- 2)( y — 1) = 0, x — y + 4 = 0.
4) Вершины ромба R и S — точки пересечения прямых L 2 и D 2 , L 1 и D 2 , соответственно, находим из уравнений:
Ответ: P (- 4, 2) R (- 6, — 2), Q (- 2, 0), S (0, 4).
Пример 2. Составить уравнения сторон треугольника, зная одну его вершину P (2, — 7), уравнения высоты 3 x + y + 11 = 0 и медианы x + 2 y + 7 = 0, проведенных из разных вершин. Решение. Для построения рисунка (рис. 4.2) приведем уравнения данных прямых к уравнениям в отрезках:
h : 3 x + y + 11 = 0, m : x + 2 y + 7 = 0 ,
План решения:1) находим уравнение прямой PQ ;2) находим координаты точки R ;3) находим уравнения прямых RP и RQ .1) Находим нормальный вектор прямой h : . Уравнение стороны PQ , проходящей через точку P (2, — 7) параллельно вектору , запишем в виде:
Находим координаты точки Q — точки пересечения прямых PQ и m :
2) По свойству медианы треугольника PQR точка S ( x S , y S ) является серединой отрезка RP . Следовательно:
Точка S лежит на медиане m , значит,
Точка R лежит на высоте h , значит,
Из последних двух уравнений определяем координаты точки R , решая систему: 3) Используя формулу (3.4), составим уравнение прямой RP , проходящей через две заданные точки R и P : Аналогично, составим уравнение прямой RQ : Ответ: x — 3 y — 23 = 0, ,
Видео:№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать
отыскать координаты вершин ромба,если известны уравнения 2-ух его сторон 2x-5y-1=0 и
Найти координаты вершин ромба,если знамениты уравнения двух его сторон 2x-5y-1=0 и 2x-5y-34=0, и уравнение одной из его диагоналей x+3y-6=0.
- Виолетта Нездрюхина
- Математика 2019-06-12 18:24:47 0 1
2x-5y-1=0
y = 2/5x-1/5 (1)
2x-5y-34=0
y = 2/5x-34/5 (2)
Прямые (1) и (2) параллельны, т.к. угловые коэффициенты равны. Значит (1) и (2) — обратные стороны ромба.
Найдём координаты точек пересечения диагонали со сторонами ромба:
1) 2/5x-1/5 = -1/3x+2 15
6x-3 = -5x+30
6x+5x = 30+3
11x = 33
x = 3
y(3) = 2/5*3-1/5 = 6/5-1/5 = 5/5 = 1
A(3; 1)
2) 2/5x-34/5 = -1/3x+2 15
6x-102 = -5x+30
6x+5x = 102+30
11x = 132
x = 12
y(12) = 2/5*12-34/5 = 24/5-34/5 = -10/5 = -2
C(12; -2)
AC — диагональ ромба. Вторая диагональ BD проходит перпендикулярно AC через её середину. Найдём точку O скрещения диагоналей. Это — середина отрезка AC.
O((3+12)/2; (1-2)/2) = (15/2; -1/2) = (7,5; -0,5)
Найдём уравнение диагонали BD. Это ровная, проходящая через точку O перпендикулярно AC. Угловой коэффициент этой прямой k = 1/3.
y-(-0,5) = -1/(-1/3) (x-7,5)
y+0,5 = 3*(x-7,5)
y+0,5 = 3x-22,5
y = 3x-23
Найдём точки скрещения диагонали BD с прямыми (1) и (2). Это и будут координаты вершин B и D.
1) 2/5x-1/5 = 3x-23 5
2x-1 = 15x-115
15x-2x = 115-1
13x = 114
x = 114/13 = 8 10/13
y(114/13) = 2/5*114/13-1/5 = 228/65-13/65 = 215/65 = 43/13 = 3 4/13
B(8 10/13; 3 4/13)
2) 2/5x-34/5 = 3x-23 5
2x-34 = 15x-115
15x-2x = 115-34
13x = 81
x = 81/13 = 6 3/13
y(81/13) = 2/5*81/13-34/5 = 162/65-442/65 = -310/65 = -62/13 = -4 10/13
D(6 3/13; -4 10/13)
Ответ: A(3; 1), B(8 10/13; 3 4/13), C(12; -2), D(6 3/13; -4 10/13)
Видео:Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать
Указания к решению заданий по алгебре 1 часть
Алгебра и аналитическая геометрия. Математический анализ
Индивидуальные задания и методические указания
для студентов ФДПО ИНО специальности 220100
Вычислительные машины, комплексы, системы и сети
УДК 519.24.001.5
Кандидат техн. наук, доцент кафедры высшей математики
Контрольные задания по алгебре и аналитической геометрии и математическому анализу для студентов ФДПО ИНО специальности 220100 Вычислительные машины, комплексы, системы и сети/ Курск. гос. техн. ун-т; Сост. Л.В.Карачевцева. Курск, 2004. 77 с.
В данной работе содержатся индивидуальные задания и методические указания, необходимые для выполнения работы.
Работа предназначена для студентов технических специальностей.
Табл. 2. Библиогр.: 11 назв.
Текст печатается в авторской редакции
ИД №06430 от 10. 12. 2001. ПЛД № 50-25 от 01. 04.97.
Подписано в печать ________ . Формат 60х84 1/16. Печать офсетная.
Усл. печ. л. 0,56. Уч.-изд. л. 0,52. Тираж 50 экз. Заказ ……….
Курский государственный технический университет.
Издательско-полиграфический центр Курского государственного технического университета. 305040 Курск, ул. 50 лет Октября, 94.
Содержание
1. Индивидуальные задания по алгебре и аналитической геометрии.……..5
2. Указания к решению заданий по алгебре и аналитической
2.1. Пример выполнения задания 1……………………………………….15
2.2. Пример выполнения задания 2……………………………………….20
2.3. Пример выполнения задания 4……………………………………….22
2.4. Пример выполнения задания 5……………………………………….27
3. Индивидуальные задания по математическому анализу……….……..33
4. Указания к выполнению заданий по математическому анализу………55
4.1. Указания к заданию 1…………..……………………………………55
4.1.1. Основные теоретические положения…………………………55
4.1.2. Пример выполнения задания 1………………………………..57
4.2. Указания к заданию 2……..…………………………………………61
4.2.1. Основные теоретические положения…………………………61
4.2.2. Пример выполнения задания 2………………………………..62
4.3. Указания к заданиям 3 и 4……..…………………………………….64
4.3.1. Основные теоретические положения…………………………64
4.3.2. Пример выполнения задания 3………………………………..66
4.3.3. Пример выполнения задания 4………………………………..67
4.4. Указания к заданию 5……..……………………………………….. 68
4.4.1. Основные теоретические положения…………………………68
4.4.2. Пример выполнения задания 5………………………………. 69
4.5. Указания к заданию 6…………..……………………………………71
4.5.1. Основные теоретические положения…………………………71
4.5.2. Пример выполнения задания 6………………………………. 73
Список рекомендуемой литературы ………………………………………77
Введение
Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом, которая состоит из следующих элементов: изучение материала по конспектам лекций и учебникам, решение задач, самопроверка усвоения материала, выполнение контрольных работ. В помощь заочникам университет организует установочные лекции, практические занятия и консультации. Однако студент должен помнить, что только при систематической и упорной самостоятельной работе помощь вуза окажется достаточно эффективной.
В процессе изучения курсов алгебры и аналитической геометрии и математического анализа студент должен выполнить контрольную работу по каждому разделу, главная цель которых — оказать студенту помощь в его работе и подготовке к экзамену. Рецензия на эти работы позволяет студенту судить о степени усвоения им материала, указывает на имеющиеся у него проблемы.
Каждая работа должна быть выполнена в отдельной тетради в клетку чернилами синего или черного цветов. Необходимо оставлять поля шириной 4-5 см для замечаний рецензента.
В заголовке работы на обложке тетради должны быть ясно написаны фамилия студента, его инициалы, учебный номер (шифр), название дисциплины. В конце работы следует поставить дату ее выполнения и подпись студента.
В контрольную работу студента должны быть включены все задания. Работа, содержащая не все задания, а также задания не своего варианта, не рассматривается.
Перед решением каждой задачи надо полностью выписать ее условие. Решение задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи. Все исправления и дополнения, на которые указал рецензент, должны быть выполнены на чистых листах в той же тетради, что и прорецензированная работа. Вносить исправления в сам текст работы после ее рецензирования запрещается.
Контрольные работы вместе со всеми исправлениями и дополнениями, сделанными по требованию рецензента, следует сохранять. Без предъявления прорецензированной контрольной работы студент не допускается к сдаче экзамена.
Индивидуальные задания по алгебре
И аналитической геометрии
Задание 1
Решить систему линейных уравнений тремя способами:
а) методом Гаусса;
б) по формулам Крамера;
в) с помощью обратной матрицы.
1. 
; 2. 
;
3. 
; 4. 
;
5. 
; 6. 
;
7. 
; 8. 
;
9. 
; 10. 
;
11. 
; 12. 
;
13. 
; 14. 
;
15. 
; 16. 
;
17. 
; 18. 
;
19. 
; 20. 
;
21. 
; 22. 
;
23. 
; 24. 
;
25. 
; 26. 
.
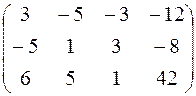
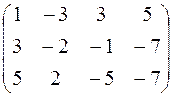
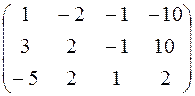
Задание 2
Решить матричное уравнение 
.
Ответ проверить подстановкой в уравнение.
1. 
.
2. 
.
3. 
.
4. 
.
5. 
.
6. 
.
7. 
.
8. 
.
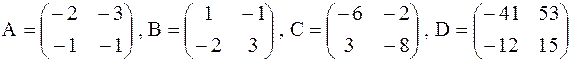
9. 
.
10. 
.
11. 
.
12. 
.
13. 
.
14. 
.
15. 
.
16. 
.
17. 
.
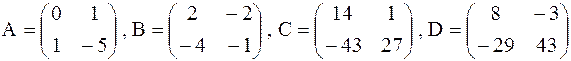
18. 
.
19. 
.
20. 
.
21. 
.
22. 
.
23. 
.
24. 
.
25. 
.
26. 
.
Задание 3
1. На прямой 
найти точку равноудаленную от двух данных точек А(1; 1), В(3; 0).
2. Найти координаты точки, симметричной точке (2; -4) относительно прямой 
.
3. Найти уравнение диагонали параллелограмма, проходящей через точку пересечения его сторон 
и 
, если известно, что диагонали параллелограмма пересекаются в точке F(-1; 0).
4. Составить уравнение прямой, проходящей через точку А(2; 6) и образующей с осями координат треугольник, который находится во второй четверти и имеет площадь 3 кв.ед.
5. Вычислить координаты вершин ромба, если известны уравнения двух его сторон 
и 
и уравнение одной из его диагоналей 
.
6. Даны уравнения одной из сторон ромба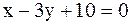 
и одной из его диагоналей 
. Диагонали ромба пересекаются в точке Р(0; 1). Найти уравнение трех остальных сторон ромба.
7. Уравнения двух сторон параллелограмма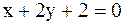 
и 
, а уравнение одной из диагоналей 
. Найти координаты вершин.
8. Даны уравнения сторон треугольника: (АВ) 7x-2y+32=0; (АС) x+ +y +2=0; (ВС) 4x+y-1=0. Найти точку пересечения его высот.
9. Даны стороны треугольника: (АС)2x-15y-55=0; (АВ)4x-3y+25=0; (ВС) 14x+3y-61=0. Составить уравнение прямой, проходящей через вершину С и через точку на стороне АВ, делящую ее (считая от вершины А) в отношении 1:4.
10.Окружность проходит через точки М(1; 0) и N(2; 1). Найти центр этой окружности, если известно, что он лежит на прямой 
.
11.Точки В(1; 2) и С(3;-6) симметричны относительно некоторой прямой. Составить уравнение этой прямой.
12.Площадь прямоугольного треугольника, катетами которого являются оси координат, равна 8. Составить уравнение гипотенузы, если известно, что она проходит через точку А(-4; 8).
13.Даны две стороны 
и 
и диагональ 
ромба. Найти вершины ромба.
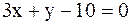
14.Найти координаты вершин параллелограмма, в котором известны две стороны 
и 
и диагональ 
.
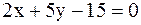
15.Две стороны треугольника заданы уравнениями 
и 
, а середина третьей стороны — точка (2;3). Составить уравнение третьей стороны.
16.Даны стороны треугольника: (АВ) 4x+3y-10=0; (ВС) 3x+2y-8=0; (АС) 8x+5y-18=0. Составить уравнение прямой, проходящей через точку С и делящей сторону АВ в отношении 2:3 (считая от вершины А).
17.Даны стороны треугольника: (АВ) 4x-3y+26=0; (АС) х+2y+1=0; (ВС) 7x+3y-37=0. Найти точку пересечения медианы, проведенной из вершины В и высоты, проходящей через вершину С.
18.Точка К отстоит на одинаковых расстояниях от точек Р(7;8) и Q(1;2). Найти координаты точки К, если известно, что она лежит на прямой 
.
19.Известны уравнения двух сторон ромба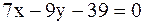 
и 
и одной из его диагоналей 
. Вычислить координаты вершин ромба.
20.Написать уравнение сторон ромба, если известны диагональ 
, точка ее пересечения с другой диагональю (0; 2) и одна из сторон 
.
21.Стороны треугольника заданы уравнениями: (АВ) 
(ВС) 3х-4y=0; (АС) 5х+12y-10=0. Найдите радиус описанной окружности.
22.Найти точку пересечения высот треугольника, стороны которого лежат на прямых 
, 
.
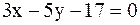
23.Даны стороны треугольника: (АС) 9x-2y-51=0; (АВ) 4x+3y+24=0; (ВС) x+2y+1=0. Составить уравнение прямой, проходящей через вершину С и точку К на стороне АВ, делящую ее в отношении 3:7 (считая от вершины В).
24.Даны уравнения сторон треугольника 
; 
, 
. Найти точку пересечения высот.
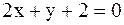
25.Даны вершины А(2;-2) и В(3;-1) и точка Р(1; 0) пересечения медиан треугольника. Составить уравнение высоты треугольника, проведенной через третью вершину С.
26.Диагонали ромба пересекаются в точке К(-2; 4). Составить уравнение диагонали, не проходящей через точку пересечения сторон 
и 
.
Задание 4
На плоскости даны точки 
, 
, 
. Сделать чертеж треугольника и найти:
а) длину и уравнение ребра ВС (записать общее, каноническое, параметрические уравнения, а также уравнения в отрезках и с угловым коэффициентом, если это возможно);
б) косинус угла А;
в) уравнение прямой, проходящей через точку А параллельно стороне ВС;
г) высоту, проведенную к стороне ВС, и ее уравнение;
д) уравнение медианы, проведенной к стороне ВС;
е) координаты центра и радиус описанной окружности;
ж) площадь треугольника;
з) центр тяжести треугольника.
Координаты точек А, В, С
| n | x1 | y1 | х2 | y2 | x3 | y3 |
| -2 | -2 | |||||
| -3 | -11 | -3 | ||||
| -7 | -7 | |||||
| -4 | -3 | -3 | ||||
| -1 | -7 | -1 | ||||
| -1 | -3 | |||||
| -9 | -11 | |||||
| -5 | -14 | |||||
| -3 | -1 | -9 | ||||
| -5 | -3 | |||||
| -9 | -9 | -5 | -5 | |||
| -7 | -3 | -7 | ||||
| -6 | -2 | -2 | ||||
| -2 | -4 | |||||
| -1 | -1 | -8 | -1 | |||
| -7 | -7 | -4 | ||||
| -6 | -14 | -6 | -8 | |||
| -7 | -2 | -2 | ||||
| -5 | -1 | -1 | -1 | |||
| -5 | -4 | |||||
| -3 | -1 | -3 | ||||
| -1 | -6 | |||||
| -9 | ||||||
| -3 | -7 | |||||
| -9 | -3 | -1 |
Задание 5
В пространстве даны точки 
, 
. Сделать схематично чертеж пирамиды SABC и найти:
а) длину и уравнения ребра АВ;
б) площадь и уравнение грани АВС;
в) высоту, проведенную из вершины S к грани АВС, и ее уравнения;
г) проекцию вершины S на плоскость АВС;
д) уравнения проекции ребра АS на грань АВС;
е) уравнения прямой, проходящей через вершину S параллельно ребру АВ;
ж) уравнение плоскости, проходящей через вершину S парал-
лельно грани АВС;
з) угол между ребрами АВ и AS;
и) угол между ребром AS и гранью АВС;
к) угол между гранями АВС и АВS;
л) координаты центра тяжести пирамиды АВСS;
м) объем пирамиды АВСS.
Значения 
| n | a1 | a2 | a3 |
| -2 | |||
| -3 | |||
| -4 | |||
| -5 | |||
| -6 | |||
| -7 | |||
| -1 | |||
| -2 | |||
| -3 | |||
| -4 | |||
| -5 | |||
| -6 | |||
| -7 | |||
| -1 | |||
| -2 | |||
| -3 | |||
| -4 | |||
| -5 | |||
| -6 | |||
| -7 | |||
| -1 | |||
| -2 | |||
| -3 | |||
| -4 | |||
| -5 | |||
| -6 |
Указания к решению заданий по алгебре
И аналитической геометрии
Пример выполнения задания 1
Решить систему линейных уравнений
.
а) методом Гаусса:
— к элементам первой и третьей строк прибавим соответствующие элементы второй строки:
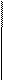
— к элементам второй строки прибавим соответствующие элементы первой строки, умноженные на -4;
— к элементам третьей строки прибавим соответствующие элементы первой строки:
🎥 Видео
№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать
Вычисляем высоту через координаты вершин 1Скачать
№974. Даны координаты вершин трапеции ABCD: А (-2; -2), В (-3; 1). Напишите уравненияСкачать
Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать
№477. Найдите диагонали ромба, если одна из них в 1,5 раза больше другой, а площадь ромбаСкачать
Уравнения стороны треугольника и медианыСкачать
Вычисление медианы, высоты и угла по координатам вершинСкачать
Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать
№976. Найдите координаты точки пересечения прямых 4x + 3y-6 = 0 и 2х+у-4 = 0.Скачать
Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать
№493. Найдите сторону и площадь ромба, если его диагонали равны 10 см и 24 см.Скачать
КАК НАЙТИ ВЕРШИНУ ПАРАБОЛЫСкачать
Найдите вершину A параллелограмма ABCD, если B(3; −4; 7), C(−5; 3; −2) и D(1; 2; −3)Скачать
№402. Даны координаты четырех вершин куба ABCDA1B1C1D1: А (0; 0; 0), В (0; 0; 1), D (0; 1; 0)Скачать
№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать
№1049. Найдите углы треугольника с вершинами А (-1; √3), В(1;-√3 )Скачать
№932. Найдите координаты вершин равнобедренного треугольника ABC, изображенного на рисункеСкачать
№980. Напишите уравнения прямых, содержащих стороны ромба, диагонали которого равны 10 см и 4 см,Скачать
