Найти координаты фокуса и уравнение директрисы параболы y 8x

Видео:Как найти ФОКУС параболы?Скачать

Задача 31453 Пожалуйста помогите 1)определить.

Условие

Пожалуйста помогите
1)определить величину параметра расположение относительно координатных оси следующих парабол: y^2=6x x^2=5y

2)найти фокус и уравнение директрисы параболы y^2=24x

Решение

Канонические уравнения параболы:
x^2=2py cимметрична относительно оси Оу, ветви направлены в сторону оси Оу
Фокус F(0;p/2)
Уравнение директрисы:
y=-p/2

x^2=-2py cимметрична относительно оси Оу, ветви направлены в сторону противоположную оси Оу
Фокус F(0;-p/2)
Уравнение директрисы:
y= p/2

y^2=2px cимметрична относительно оси Ох, ветви направлены в сторону оси Ох
Фокус F(p/2;0)
Уравнение директрисы:
x=-p/2

y^2=-2px cимметрична относительно оси Ох, ветви направлены в сторону противоположную оси Ох
Фокус F(-p/2;0)
Уравнение директрисы:
x=p/2

[b]Решение[/b]:
1) y^2=6x ⇒ 2p=6;
p=3
cимметрична относительно оси Ох, ветви направлены в сторону оси Ох

x^2=5y 2p=5 ⇒ 2p=5;
p=2,5
cимметрична относительно оси Оу, ветви направлены в сторону оси Оу

2)
y^2=24x ⇒ 2p=24;
p=12
cимметрична относительно оси Ох, ветви направлены в сторону оси Ох

Фокус F(12;0)
Уравнение директрисы:
x=-12

см. рис.3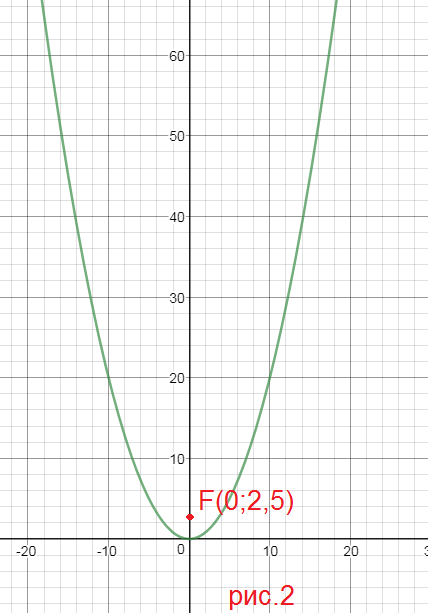

Видео:Фокус и директриса параболы 1Скачать

Практическая работа по высшей математике на тему: «Парабола. Решение задач»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Дисциплина – «Элементы высшей математики»

Видео:213. Фокус и директриса параболы.Скачать

Тема: «Кривые второго порядка. Парабола»

Цель: формирование умений составлять уравнения параболы, исследовать форму и расположение параболы;

формирование общих компетенций, включающими в себя способность:

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.

ОК 6. Работать в коллективе и в команде, эффективно общаться с коллегами, руководством, потребителями.

Методические указания и теоретические сведения к практической работе

Парабола — геометрическое место точек , равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).

Наряду с эллипсом и гиперболой , парабола является коническим сечением . Она может быть определена как коническое сечение с единичным эксцентриситетом .

Точка параболы, ближайшая к её директрисе, называется вершиной этой параболы. Вершина является серединой перпендикуляра, опущенного из фокуса на директрису.

(или , если поменять местами оси).

Число p называется фокальным параметром, оно равно расстоянию от фокуса до директрисы. Поскольку каждая точка параболы равноудалена от фокуса и директрисы, то и вершина — тоже, поэтому она лежит между фокусом и директрисой на расстоянии от обоих.

Парабола, заданная квадратичной функцией

Квадратичная функция при также является уравнением параболы и графически изображается той же параболой, что и но в отличие от последней имеет вершину не в начале координат, а в некоторой точке A, координаты которой вычисляются по формулам:

где — дискриминант квадратного трёхчлена.

Общее уравнение параболы

В общем случае парабола не обязана иметь ось симметрии, параллельную одной из координатных осей. Однако, как и любое другое коническое сечение, парабола является кривой второго порядка и, следовательно, её уравнение на плоскости в декартовой системе координат может быть записано в виде квадратного многочлена:

Если кривая второго порядка, заданная в таком виде, является параболой, то составленный из коэффициентов при старших членах дискриминант равен нулю.

Пример 1. Найти координаты фокуса и уравнение директрисы параболы, заданной уравнением .

Решение. Из данного канонического уравнения параболы следует, что , т.е. ,откуда .Значит, точка — фокус параболы, а — уравнение ее директрисы.

Пример 2. Составить каноническое уравнение параболы и уравнение ее директрисы, если известно, что вершина параболы лежит в начале координат, а фокус имеет координаты .

Решение. Согласно условию, фокус параболы расположен на отрицательной полуоси , т.е. ее уравнение имеет вид: x 2 = — 2 py

Так как , то , откуда .Итак, уравнение параболы есть , а уравнение ее директрисы .

Пример 3. Составить уравнение параболы, имеющей вершину в начале координат, симметричной оси Ох и проходящей через точку .

Решение. Из условия заключаем, что уравнение параболы следует искать в виде .

Так как точка принадлежит параболе , то ее координаты удовлетворяют этому уравнению: 36= — 2р*(-3); 2р=12.

Итак, уравнение параболы имеет вид .

Пример 4. Парабола симметрична относительно оси Ox , проходит через точку

A (4, -1), а вершина ее лежит в начале координат. Составить ее уравнение.

Решение. Так как парабола проходит через точку A (4, -1) с положительной абсциссой, а ее осью служит ось Ox , то уравнение параболы следует искать в виде y 2 = 2 px . Подставляя в это уравнение координаты точки A , будем иметь

искомым уравнением будет

Эскиз этой параболы показан на рисунке

Пример 5. Парабола y 2 = 2 px проходит через точку A (2, 4). Определить ее параметр p .

Решение. Подставляем в уравнение параболы вместо текущих координат координаты точки A (2, 4). Получаем

4 2 = 2 p *2; 16 = 4 p ; p = 4.

Пример 6. Привести к каноническому (простейшему) виду уравнение параболы

y = 2 x 2 + 4 x + 5 и найти координаты ее вершины.

Решение. Уравнение y = 2 x 2 + 4 x + 5 преобразуем, выделив в правой части полный квадрат:

пусть теперь x ₁ = x + 1, y ₁ = y — 3. Из сравнения с формулами

координаты нового начала: x ₀ = -1; y ₀ = 3. Уравнение параболы примет вид

Эскиз параболы показан на рисунке.

Пример 7. Упростить уравнение параболы y = x 2 — 7 x + 12, найти координаты ее вершины и начертить эскиз кривой.

Решение. Выделим в правой части уравнения y = x 2 — 7x + 12 полный квадрат по способу, указанному выше в задаче , и получим

Отсюда из сравнения с формулами

координаты нового начала, т. е. вершины параболы, будут . После переноса начала координат в точку уравнение параболы примет наиболее простой вид . Эскиз кривой представлен на рисунке.

Пример 8. Составить уравнение параболы и ее директрисы, если парабола проходит через точки пересечения прямой и окружности и симметрична относительно оси .

Решение. Найдем точки пересечения заданных линий, решив совместно их уравнения:

В результате получим два решения и . Точки пересечения и . Так как парабола проходит через точку и симметрична относительно оси , то в этой точке будет находиться вершина параболы. Поэтому уравнение параболы имеет вид . Так как парабола проходит через точку , то координаты этой точки удовлетворяют уравнению параболы: , ,

Итак, уравнением параболы будет , уравнение директрисы или , откуда

Ответ. ;

Пример 9. Мостовая арка имеет форму параболы. Определить параметр этой параболы, зная, что пролет арки равен , а высота

Решение. В ыберем прямоугольную систему координат так, чтобы вершина параболы (мостовой арки) находилась в начале координат, а ось симметрии совпадала с отрицательным направлением оси . В таком случае каноническое уравнение параболы имеет вид , а концы хорды арки и . Подставив координаты одного из концов хорды (например, ) в уравнение параболы и решив полученное уравнение относительно , получим

Ответ.

а) Найти координаты фокуса и уравнение директрисы параболы, заданной уравнением у 2 =16р .

б) Найти координаты фокуса и уравнение директрисы параболы, заданной уравнением

а) Составить каноническое уравнение параболы и уравнение ее директрисы, если известно, что вершина параболы лежит в начале координат, а фокус имеет координаты (0; -7).

б) Составить каноническое уравнение параболы и уравнение ее директрисы, если известно, что вершина параболы лежит в начале координат, а фокус имеет координаты (0; 4).

а) Составить уравнение параболы, имеющей вершину в начале координат, симметричной относительно оси Ох и проходящей через точку А (-2; — 4) . Начертить эскиз данной кривой.

б) Составить уравнение параболы, имеющей вершину в начале координат, симметричной относительно оси Ох и проходящей через точку А (3; — 5) . Начертить эскиз данной кривой.

а) Парабола y 2 = 2 px проходит через точку A (4; 8). Определить ее параметр p .

б) Парабола y 2 = — 2 px проходит через точку A (-4; -8). Определить ее параметр p .

а) Привести к каноническому (простейшему) виду уравнение параболы y = 2 x 2 + 8 x + 5 и найти координаты ее вершины. Начертить эскиз данной кривой.

б) Привести к каноническому (простейшему) виду уравнение параболы y = 4 x 2 + 16 x +10 и найти координаты ее вершины. Начертить эскиз данной кривой.

Задание 6. а) Составить уравнение параболы и ее директрисы, если парабола проходит через точки пересечения прямой 2х + 2у=0 и окружности х 2 +у 2 – 4х=0 и симметрична относительно оси Оу.

б) Составить уравнение параболы и ее директрисы, если парабола проходит через точки пересечения прямой 3х + 3у=0 и окружности 2х 2 + 2у 2 — 8х=0 и симметрична относительно оси Ох .

Задание 7. а) Арка здания имеет форму параболы. Определить параметр р этой параболы, зная, что пролет арки равен 12 м, а высота 4 м.

б) Арка дома имеет форму параболы. Определить параметр р этой параболы, зная, что пролет арки равен 14 м, а высота 6 м.

Отчет о практической работе

Тема практической работы

Цель практической работы

В ходе выполнения практической работы я научился (закрепил умения) вычислять…

Я получил (совершенствовал) практические навыки…

В ходе практической работы я получил новые знания. Узнал, что …

Мне было сложно выполнять…, потому, что…

Мне было несложно выполнять…, потому, что…

Краткое описание документа:

Практическая работа по высшей математике на тему: «Парабола. Решение задач». В работе представлены краткие теоретические сведения и методические указания для выполнения практической работы. Работа предназначена студентам 2 курса СПО. Может быть использована для аудиторной и внеаудиторной самостоятельной работы студентов 2 курса СПО.

Видео:КАК НАЙТИ ВЕРШИНУ ПАРАБОЛЫСкачать

Парабола

Видео:Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Парабола, её форма, фокус и директриса.

Параболой называется линия, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
y^=2pxlabel
$$
при условии (p > 0).

Из уравнения eqref вытекает, что для всех точек параболы (x geq 0). Парабола проходит через начало канонической системы координат. Эта точка называется вершиной параболы.

Форма параболы известна из курса средней школы, где она встречается в качестве графика функции (y=ax^). Отличие уравнений объясняется тем, что в канонической системе координат по сравнению с прежней оси координат поменялись местами, а коэффициенты связаны равенством (2p=a^).

Фокусом параболы называется точка (F) с координатами ((p/2, 0)) в канонической системе координат.

Директрисой параболы называется прямая с уравнением (x=-p/2) в канонической системе координат ((PQ) на рис. 8.11).

Рис. 8.11. Парабола.

Видео:Фокус и директриса параболы 2Скачать

Свойства параболы.

Расстояние от точки (M(x, y)), лежащей на параболе, до фокуса равно
$$
r=x+frac

.label
$$

Вычислим квадрат расстояния от точки (M(x, y)) до фокуса по координатам этих точек: (r^=(x-p/2)^+y^) и подставим сюда (y^) из канонического уравнения параболы. Мы получаем
$$
r^=left(x-frac

right)^+2px=left(x+frac

right)^.nonumber
$$
Отсюда в силу (x geq 0) следует равенство eqref.

Заметим, что расстояние от точки (M) до директрисы также равно
$$
d=x+frac

.nonumber
$$

Следовательно, мы можем сделать следующий вывод.

Для того чтобы точка (M) лежала на параболе, необходимо и достаточно, чтобы она была одинаково удалена от фокуса и от директрисы этой параболы.

Докажем достаточность. Пусть точка (M(x, y)) одинаково удалена от фокуса и от директрисы параболы:
$$
sqrt<left(x-frac

right)^+y^>=x+frac

.nonumber
$$

Возводя это уравнение в квадрат и приводя в нем подобные члены, мы получаем из него уравнение параболы eqref. Это заканчивает доказательство.

Параболе приписывается эксцентриситет (varepsilon=1). В силу этого соглашения формула
$$
frac=varepsilonnonumber
$$
верна и для эллипса, и для гиперболы, и для параболы.

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Уравнение касательной к параболе.

Выведем уравнение касательной к параболе в точке (M_(x_, y_)), лежащей на ней. Пусть (y_ neq 0). Через точку (M_) проходит график функции (y=f(x)), целиком лежащий на параболе. (Это (y=sqrt) или же (y=-sqrt), смотря по знаку (y_).) Для функции (f(x)) выполнено тождество ((f(x))^=2px), дифференцируя которое имеем (2f(x)f'(x)=2p). Подставляя (x=x_) и (f(x_)=y_), находим (f'(x_)=p/y_) Теперь мы можем написать уравнение касательной к параболе
$$
y-y_=frac

<y_>(x-x_).nonumber
$$
Упростим его. Для этого раскроем скобки и вспомним, что (y_^=2px_). Теперь уравнение касательной принимает окончательный вид
$$
yy_=p(x+x_).label
$$

Заметим, что для вершины параболы, которую мы исключили, положив (y_ neq 0), уравнение eqref превращается в уравнение (x=0), то есть в уравнение касательной в вершине. Поэтому уравнение eqref справедливо для любой точки на параболе.

Касательная к параболе в точке (M_) есть биссектриса угла, смежного с углом между отрезком, который соединяет (M_) с фокусом, и лучом., выходящим из этой точки в направлении оси параболы (рис. 8.12).

Рассмотрим касательную в точке (M_(x_, y_)). Из уравнения eqref получаем ее направляющий вектор (boldsymbol(y_, p)). Значит, ((boldsymbol, boldsymbol_)=y_) и (cos varphi_=y_/boldsymbol). Вектор (overrightarrow<FM_>) имеет компоненты (x_=p/2) и (y_), а потому
$$
(overrightarrow<FM_>, boldsymbol)=x_y_-frac

y_+py_=y_(x_+frac

).nonumber
$$
Но (|overrightarrow<FM_>|=x_+p/2). Следовательно, (cos varphi_=y_/|boldsymbol|). Утверждение доказано.

Заметим, что (|FN|=|FM_|) (см. рис. 8.12).

📺 Видео

Видеоурок "Парабола"Скачать

Построение параболы по ее директрисе и фокусуСкачать

Параболы. ПримерСкачать

165. Найти фокусы и эксцентриситет эллипса.Скачать

Как найти вершину параболы?Скачать

Квадратичная функция. Вершина параболы и нули функции. 8 класс.Скачать

Как легко составить уравнение параболы из графикаСкачать

ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Парабола (часть 1). Каноническое уравнение параболы. Высшая математика.Скачать

Парабола. Квадратичная функцияСкачать

Вычисление фокуса параболыСкачать

Фокус и директриса параболы 2Скачать

Построение параболыСкачать