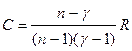Найти для ван дер ваальсовского газа уравнение адиабаты в переменных t v

(б) Мы используем

Так что, $dQ = C_dT + fracdV$

Таким образом, по постоянной $p$, $C_

= C_ + frac left ( frac right )_

$

Таким образом $C_

— C_ = frac left ( frac right )_

$, Bit $p = frac — frac <V^>$

Дифференцируя, $0 = left ( — frac <(V — b)^> + frac <V^> right ) left ( frac right )_

+ frac$

Видео:Уравнение Ван-дер-Ваальса | Газы.Молекулярно-кинетическая теория | Химия (видео 8)Скачать

Первое начало термодинамики.

Теплоемкость.

· Первое начало термодинамики:

где Q — количество тепла, сообщенное системе; А — работа, совершаемая системой; ΔU — приращение внутренней энергии системы.

· Работа, совершаемая газом:

где C_p, C_V — молярные теплоемкости при постоянных давлении и объеме соответственно.

· Внутренняя энергия идеального газа:

· Молярная теплоемкость идеального газа при политропическом про­цессе:

· Внутренняя энергия моля газа Ван — дер — Ваальса:

2.1. Газообразный водород, находящийся при нормальных условиях в закрытом сосуде объемом V = 5 л. охладили на ΔT = 55 K. Найти приращение внутренней энергии газа и количество отданного им тепла.

Ответ: 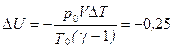кДж;

2.2. Какое количество тепла надо сообщить азоту при изобарическом нагревании, чтобы газ совершил работу A, равную 2 Дж?

Ответ: Дж.

2.3. Газ, занимающий объем 5 л и находящийся под давлением 2·10 2 Н/м 2 при температуре 17 о C, был нагрет и расширялся изобарически. Работа расширения газа при этом оказалась равной 196 Нм. На сколько нагрели газ?

Ответ: K

2.4.На нагревание 40 г кислорода от 16 о Cдо40 о Cзатрачено 150 кал. При каких условиях нагре­вался газ? (При постоянном объеме или при постоянном давлении?)

Ответ: при постоянном объеме, т. к.

Дж; Дж.

2.5. Найти молярную массу газа μ, если при нагревании m = 0,5 кг этого газа на ΔT = 10 K изобарически требуется на ΔQ = 1,48 кДжтепла больше, чем при изохорическом нагревании.

2.6. Один моль некоторого идеального газа изобарически нагрели на ΔT = 72 K, сообщив ему количество тепла Q = 1,6 кДж.Найти прира­щение его внутренней энергии и величину γ = С_p/C_V.

2.7. Вычислить γдля газовой смеси, состоящей из v₁= 2 моля кисло­рода и v₂ = 3 моля углекислого газа. Газы считать идеальными.

2.8. Вычислить удельные теплоемкости C_p и С_V для газовой смеси, состоящей из 7 г азота и 20 г аргона. Газы идеальные.

2.9.Найти удельные теплоемкости c_v и c_p некоторого газа, если известно, что масса одного киломоля этого газа равна μ = 30 кг/кмоль и отношение γ = c_p/c_v = 1,4.

Дж/кг; Дж/кг.

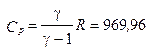
2.10.При изобарическом расширении кислорода им была совершена работа A = 2·10 -6 Дж. Оп­ределить изменение внутренней энергии ΔU этого количества газа, количество тепла Q, сообщенного ему в процессе расширения, а также массу газа m, если его температура возросла на 10 о . Газ считать идеальным.

Ответ: ;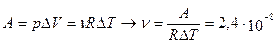

мкг;

2.11.Газ находится в вертикально расположенном цилиндре с площадью дна s = 10 см 2 . Пор­шень, закрывающий цилиндр, имеет массу 10 кги может перемещаться в цилиндре без трения. Начальный объем газа 8 л, температура 10 о С. Какое количество тепла необхо­димо затратить для того, чтобы нагреть газ при этих условиях на 25 о С, если известно, что теплоемкость C_V этой массы газа, измеренная при закрепленном в начальном положении поршне, оказалась равной 25 дж/град? Давление наружного воздуха не учитывать.

Ответ: 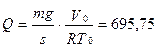Дж.

2.12.В сосуде под поршнем находится m₀ = 10 г азота. 1) Какое количество тепла Q надо затратить, чтобы нагреть азот на Δt o = 20 о С? 2) На сколько при этом поднимается поршень? Масса поршня m = 1 кг, площадь поперечного сечения s = 10 см 2 . Давление над поршнем равно 1 атм.

Ответ: Q = νCΔt o = 20785 Дж; м.

2.13.2 л азота находятся под давлением 10 5 н/м 2 . Какое количество тепла надо сообщить азоту, чтобы при p = const объем увеличить вдвое?

2.14.2 л азота находятся под давлением 10 5 н/м 2 . Какое количество тепла надо сообщить азоту, чтобы при V = const давление увеличить вдвое?

2.15. Найти молярную теплоемкость идеального газа при политропическом процессе pV n = соnst, если показатель адиабаты газа равен γ. При каких значениях показателя политропы n теплоемкость газа будет отрицательной?

2.17. Один моль идеального газа, теплоемкость которого при постоян­ном давлении С_p, совершает процесс по закону p = р₀ + α/V, где р₀, α — постоянные. Найти:

а) теплоемкость газа как функцию его объема V;

б) сообщенное газу тепло при его расширении от V₁до V₂.

2.18. Найти уравнение процесса (в переменных Т, V). при котором молярная теплоемкость идеального газа изменяется по закону:

2.19. Один моль кислорода, находившегося при температуре T₀ = 290 K, адиабатически сжали так, что его давление возросло в η = 10 раз. Найти:

а) температуру газа после сжатия;

б) работу, которая была совершена над газом.

2.20. Некоторую массу азота сжали в η = 5 раз (по объему) один раз адиабатически, другой раз изотермически. Начальное состояние газа в обоих случаях одинаково. Найти отношение соответствующих работ, затраченных на сжатие.

Ответ: При адиабатическом сжатии работа больше в

n = (η γ -1 – 1)/(γ – 1)lnη = 1,4 раза.

2.21. Объем моля идеального газа с показателем адиабаты γ изменяют по закону V = а/Т. где а — постоянная. Найти количество тепла, получен­ное газом в этом процессе, если его температура испытала приращение ΔT.

2.22.Найти работу, совершаемую одним молем ван-дер-ваальсовского газа при изотермическом расширении его объема от V₁ до V₂ при температуре Т.

2.23. Один моль кислорода расширили от объема V₁ = 1 л: до V₂ = 5 л при постоянной температуре Т = 280 K. Вычислить количество погло­щенного газом тепла. (Газ считать ван-дер-ваальсовским.)

2.24. Найти для ван-дер-ваальсовского газа уравнение адиабаты в переменных (T, V), если его теплоемкость при постоянном объеме равна C_V.

2.25.Определить для ван-дер-ваальсовского газа разность моляр­ных теплоемкостей C_p – С_V.

2.27. Показать, что если уравнение состояния имеет вид p = p(T, V), то справедливо соотношение: рα_р = Kα_V, где

α_р = (др/дТ)_V/р — тепло­вой коэффициент давления при постоянном объеме,

α_V = (дV/дT)_p/V — коэффициент теплового расширения при постоянном давлении,

K = -V(др/дV)_Т — изотермический модуль упругости.

2.28. В цилиндре, закрытом с обоих концов и наполненном воздухом, находится поршень, разделяющий пространство в цилиндре на две рав­ные части. Давление воздуха по обе стороны поршня равно p₀= 105 Пa. Поршень начинает совершать малые колебания, причем процесс в га­зе считаем адиабатическим. Масса поршня m = 1,5 кг, расстояние от стенки до поршня l = 20 см. площадь поршня S = 100 см 2 . Трением пре­небрегаем. Определить период колебаний поршня.

Ответ: 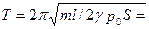0,05 с.

2.29 Моль идеального газа находится в неограниченном вертикальном цилиндре, помещенном в однородное поле тяжести. Найти теплоемкость газа.

2.30.Рассматривая воздух как идеальный газ, показать, что при на­гревании воздуха, находящегося в комнате, его внутренняя энергия не меняется, если только внешнее давление остается постоянным.

Ответ: результат следует из формулы U = С_VPV/R.

2.31.С какой высоты упал медный шар, если при столкновении с почвой его температура по­высилась с 20 о С до 23 о С?Считать, что выделившееся в результате столкновения коли­чество теплоты распределилось между медным шаром и почвой в соотношении 1:2. Со­противлением воздуха пренебречь. С_м = 390 Дж/(кг∙К).

2.32.Внутренняя энергия теплового излучения в замкнутой полости с объемом V определяется выражением U = Vu,где плотность энергии и = аТ 4 (постоянная а > 0), а давление излучения определяется уравнением состояния p = u/3. Найти уравнение адиабатического процесса.

Видео:Адиабатный процесс. 10 класс.Скачать

Адиабатический процесс и уравнения адиабаты для идеального газа. Пример задачи

Адиабатический переход между двумя состояниями в газах не относится к числу изопроцессов, тем не менее, он играет важную роль не только в различных технологических процессах, но и в природе. В данной статье рассмотрим, что представляет собой этот процесс, а также приведем уравнения адиабаты идеального газа.

Видео:Урок 194. Уравнение Ван-дер-ВаальсаСкачать

Кратко об идеальном газе

Идеальным называется такой газ, в котором нет взаимодействий между его частицами, и их размеры равны нулю. В природе, конечно же, не существует идеальных на сто процентов газов, поскольку все они состоят из имеющих размеры молекул и атомов, которые взаимодействуют друг с другом всегда как минимум с помощью ван-дер-ваальсовых сил. Тем не менее, описанная модель часто выполняется с достаточной для решения практических задач точностью для многих реальных газов.

Вам будет интересно: Атеизм и антиклерикализм — это. В чем отличие понятий

Главным уравнением идеального газа является закон Клапейрона-Менделеева. Он записывается в следующей форме:

Это уравнение устанавливает прямую пропорциональность между произведением давления P на объем V и количества вещества n на абсолютную температуру T. Величина R — газовая константа, которая играет роль коэффициента пропорциональности.

Видео:Реальный газ Уравнение Ван-Дер-ВаальсаСкачать

Что это адиабатический процесс?

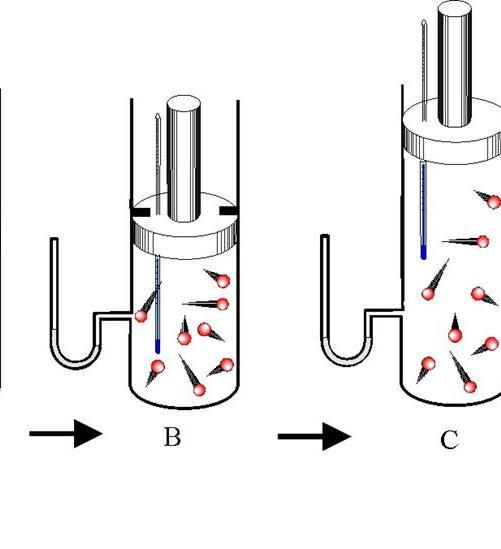
Адиабатический процесс — это такой переход между состояниями газовой системы, при котором обмена энергией с внешней средой не происходит. При этом изменяются все три термодинамических характеристики системы (P, V, T), а количество вещества n остается постоянным.

Различают адиабатическое расширение и сжатие. Оба процесса происходят только за счет внутренней энергии системы. Так, в результате расширения давление и особенно температура системы сильно падают. Наоборот, адиабатическое сжатие приводит к положительному скачку температуры и давления.

Чтобы не происходил обмен теплом между окружающей средой и системой, последняя должна обладать теплоизолированными стенками. Кроме того, сокращение длительности протекания процесса значительно уменьшает тепловой поток от и к системе.

Видео:Термодинамика - Лекция 3Скачать

Уравнения Пуассона для адиабатического процесса

Первый закон термодинамики записывается в таком виде:

Иными словами, сообщенная системе теплота Q идет на выполнение системой работы A и на повышение ее энергии внутренней ΔU. Чтобы написать уравнение адиабаты, следует положить Q=0, что соответствует определению изучаемого процесса. Получаем:

При изохорном процессе в идеальном газе все тепло идет на повышение внутренней энергии. Этот факт позволяет записать равенство:

Где CV — изохорная теплоемкость. Работа A, в свою очередь, вычисляется так:

Где dV — малое изменение объема.

Помимо уравнения Клапейрона-Менделеева, для идеального газа справедливо следующее равенство:

Где CP — изобарная теплоемкость, которая всегда больше изохорной, так как она учитывает потери газа на расширение.

Анализируя записанные выше равенства и проводя интегрирование по температуре и объему, приходим к следующему уравнению адиабаты:

Здесь γ — это показатель адиабаты. Он равен отношению изобарной теплоемкости к изохорной. Это равенство называется уравнением Пуассона для процесса адиабатического. Применяя закон Клапейрона-Менделеева, можно записать еще два аналогичных выражения, только уже через параметры P-T и P-V:

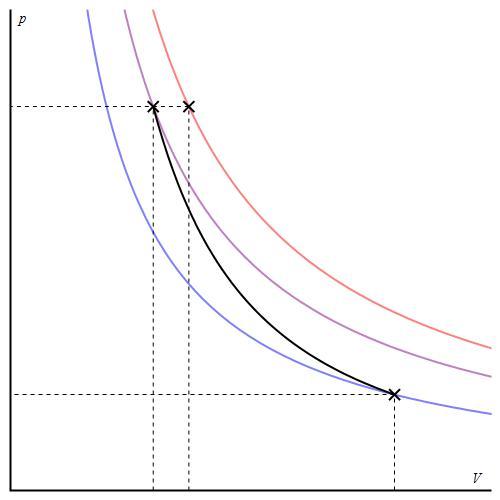
График адиабаты можно привести в различных осях. Ниже он показан в осях P-V.

Цветные линии на графике соответствуют изотермам, черная кривая — это адиабата. Как видно, адиабата ведет себя более резко, чем любая из изотерм. Этот факт просто объяснить: для изотермы давление меняется обратно пропорционально объему, для изобаты же давление изменяется быстрее, поскольку показатель γ>1 для любой газовой системы.

Видео:Физика. Термодинамика: Адиабатный процесс. Центр онлайн-обучения «Фоксфорд»Скачать

Пример задачи

В природе в горной местности, когда воздушная масса движется вверх по склону, то ее давление падает, она увеличивается в объеме и охлаждается. Этот адиабатический процесс приводит к снижению точки росы и к образованию жидких и твердых осадков.

Предлагается решить следующую задачу: в процессе подъема воздушной массы по склону горы давление упало на 30 % по сравнению с давлением у подножия. Чему стала равна ее температура, если у подножия она составляла 25 oC?

Для решения задачи следует использовать следующее уравнение адиабаты:

Его лучше записать в таком виде:

Если P1 принять за 1 атмосферу, то P2 будет равно 0,7 атмосферы. Для воздуха показатель адиабаты равен 1,4, поскольку его можно считать двухатомным идеальным газом. Значение температуры T1 равно 298,15 К. Подставляя все эти числа в выражение выше, получаем T2 = 269,26 К, что соответствует -3,9 oC.

🔥 Видео

Уравнение Ван-дер-Ваальса (вывод и применение). By Bogatov N.A.Скачать

29. Адиабатический процесс. Уравнение ПуассонаСкачать

Уравнение состояния идеального газа. 10 класс.Скачать

35. Реальные газыСкачать

Реальные газы. Изотермы Эндрюса и Ван-Дер-Ваальса. Метастабильные состоянияСкачать

Уравнение Ван дер Ваальса. Часть 3. Внутренняя энергия реального газа. Фазовые переходы 1 рода.Скачать

Урок 172. Применение 1 закона термодинамики для различных процессовСкачать

Адиабатное расширениеСкачать

Физика 10 класс. Адиабатный процесс.Скачать

Семинар №6 "Газ Ван-дер-Ваалса. Течение газов" (Гавриков А.В.)Скачать

Консультация по термодинамике. Часть 3Скачать

Лекция №7 "Газ Ван-дер-Ваальса. Эффект Джоуля-Томсона" (Овчинкин В.А.)Скачать