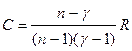Найти для ван дер ваальсовского газа уравнение адиабаты

(б) Мы используем

Так что, $dQ = C_dT + fracdV$

Таким образом, по постоянной $p$, $C_

= C_ + frac left ( frac right )_

$

Таким образом $C_

— C_ = frac left ( frac right )_

$, Bit $p = frac — frac <V^>$

Дифференцируя, $0 = left ( — frac <(V — b)^> + frac <V^> right ) left ( frac right )_

+ frac$

Видео:Адиабатный процесс. 10 класс.Скачать

Первое начало термодинамики.

Теплоемкость.

· Первое начало термодинамики:

где Q — количество тепла, сообщенное системе; А — работа, совершаемая системой; ΔU — приращение внутренней энергии системы.

· Работа, совершаемая газом:

где C_p, C_V — молярные теплоемкости при постоянных давлении и объеме соответственно.

· Внутренняя энергия идеального газа:

· Молярная теплоемкость идеального газа при политропическом про­цессе:

· Внутренняя энергия моля газа Ван — дер — Ваальса:

2.1. Газообразный водород, находящийся при нормальных условиях в закрытом сосуде объемом V = 5 л. охладили на ΔT = 55 K. Найти приращение внутренней энергии газа и количество отданного им тепла.

Ответ: 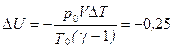кДж;

2.2. Какое количество тепла надо сообщить азоту при изобарическом нагревании, чтобы газ совершил работу A, равную 2 Дж?

Ответ: Дж.

2.3. Газ, занимающий объем 5 л и находящийся под давлением 2·10 2 Н/м 2 при температуре 17 о C, был нагрет и расширялся изобарически. Работа расширения газа при этом оказалась равной 196 Нм. На сколько нагрели газ?

Ответ: K

2.4.На нагревание 40 г кислорода от 16 о Cдо40 о Cзатрачено 150 кал. При каких условиях нагре­вался газ? (При постоянном объеме или при постоянном давлении?)

Ответ: при постоянном объеме, т. к.

Дж; Дж.

2.5. Найти молярную массу газа μ, если при нагревании m = 0,5 кг этого газа на ΔT = 10 K изобарически требуется на ΔQ = 1,48 кДжтепла больше, чем при изохорическом нагревании.

2.6. Один моль некоторого идеального газа изобарически нагрели на ΔT = 72 K, сообщив ему количество тепла Q = 1,6 кДж.Найти прира­щение его внутренней энергии и величину γ = С_p/C_V.

2.7. Вычислить γдля газовой смеси, состоящей из v₁= 2 моля кисло­рода и v₂ = 3 моля углекислого газа. Газы считать идеальными.

2.8. Вычислить удельные теплоемкости C_p и С_V для газовой смеси, состоящей из 7 г азота и 20 г аргона. Газы идеальные.

2.9.Найти удельные теплоемкости c_v и c_p некоторого газа, если известно, что масса одного киломоля этого газа равна μ = 30 кг/кмоль и отношение γ = c_p/c_v = 1,4.

Дж/кг; Дж/кг.

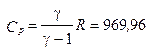
2.10.При изобарическом расширении кислорода им была совершена работа A = 2·10 -6 Дж. Оп­ределить изменение внутренней энергии ΔU этого количества газа, количество тепла Q, сообщенного ему в процессе расширения, а также массу газа m, если его температура возросла на 10 о . Газ считать идеальным.

Ответ: ;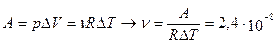

мкг;

2.11.Газ находится в вертикально расположенном цилиндре с площадью дна s = 10 см 2 . Пор­шень, закрывающий цилиндр, имеет массу 10 кги может перемещаться в цилиндре без трения. Начальный объем газа 8 л, температура 10 о С. Какое количество тепла необхо­димо затратить для того, чтобы нагреть газ при этих условиях на 25 о С, если известно, что теплоемкость C_V этой массы газа, измеренная при закрепленном в начальном положении поршне, оказалась равной 25 дж/град? Давление наружного воздуха не учитывать.

Ответ: 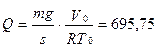Дж.

2.12.В сосуде под поршнем находится m₀ = 10 г азота. 1) Какое количество тепла Q надо затратить, чтобы нагреть азот на Δt o = 20 о С? 2) На сколько при этом поднимается поршень? Масса поршня m = 1 кг, площадь поперечного сечения s = 10 см 2 . Давление над поршнем равно 1 атм.

Ответ: Q = νCΔt o = 20785 Дж; м.

2.13.2 л азота находятся под давлением 10 5 н/м 2 . Какое количество тепла надо сообщить азоту, чтобы при p = const объем увеличить вдвое?

2.14.2 л азота находятся под давлением 10 5 н/м 2 . Какое количество тепла надо сообщить азоту, чтобы при V = const давление увеличить вдвое?

2.15. Найти молярную теплоемкость идеального газа при политропическом процессе pV n = соnst, если показатель адиабаты газа равен γ. При каких значениях показателя политропы n теплоемкость газа будет отрицательной?

2.17. Один моль идеального газа, теплоемкость которого при постоян­ном давлении С_p, совершает процесс по закону p = р₀ + α/V, где р₀, α — постоянные. Найти:

а) теплоемкость газа как функцию его объема V;

б) сообщенное газу тепло при его расширении от V₁до V₂.

2.18. Найти уравнение процесса (в переменных Т, V). при котором молярная теплоемкость идеального газа изменяется по закону:

2.19. Один моль кислорода, находившегося при температуре T₀ = 290 K, адиабатически сжали так, что его давление возросло в η = 10 раз. Найти:

а) температуру газа после сжатия;

б) работу, которая была совершена над газом.

2.20. Некоторую массу азота сжали в η = 5 раз (по объему) один раз адиабатически, другой раз изотермически. Начальное состояние газа в обоих случаях одинаково. Найти отношение соответствующих работ, затраченных на сжатие.

Ответ: При адиабатическом сжатии работа больше в

n = (η γ -1 – 1)/(γ – 1)lnη = 1,4 раза.

2.21. Объем моля идеального газа с показателем адиабаты γ изменяют по закону V = а/Т. где а — постоянная. Найти количество тепла, получен­ное газом в этом процессе, если его температура испытала приращение ΔT.

2.22.Найти работу, совершаемую одним молем ван-дер-ваальсовского газа при изотермическом расширении его объема от V₁ до V₂ при температуре Т.

2.23. Один моль кислорода расширили от объема V₁ = 1 л: до V₂ = 5 л при постоянной температуре Т = 280 K. Вычислить количество погло­щенного газом тепла. (Газ считать ван-дер-ваальсовским.)

2.24. Найти для ван-дер-ваальсовского газа уравнение адиабаты в переменных (T, V), если его теплоемкость при постоянном объеме равна C_V.

2.25.Определить для ван-дер-ваальсовского газа разность моляр­ных теплоемкостей C_p – С_V.

2.27. Показать, что если уравнение состояния имеет вид p = p(T, V), то справедливо соотношение: рα_р = Kα_V, где

α_р = (др/дТ)_V/р — тепло­вой коэффициент давления при постоянном объеме,

α_V = (дV/дT)_p/V — коэффициент теплового расширения при постоянном давлении,

K = -V(др/дV)_Т — изотермический модуль упругости.

2.28. В цилиндре, закрытом с обоих концов и наполненном воздухом, находится поршень, разделяющий пространство в цилиндре на две рав­ные части. Давление воздуха по обе стороны поршня равно p₀= 105 Пa. Поршень начинает совершать малые колебания, причем процесс в га­зе считаем адиабатическим. Масса поршня m = 1,5 кг, расстояние от стенки до поршня l = 20 см. площадь поршня S = 100 см 2 . Трением пре­небрегаем. Определить период колебаний поршня.

Ответ: 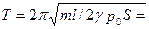0,05 с.

2.29 Моль идеального газа находится в неограниченном вертикальном цилиндре, помещенном в однородное поле тяжести. Найти теплоемкость газа.

2.30.Рассматривая воздух как идеальный газ, показать, что при на­гревании воздуха, находящегося в комнате, его внутренняя энергия не меняется, если только внешнее давление остается постоянным.

Ответ: результат следует из формулы U = С_VPV/R.

2.31.С какой высоты упал медный шар, если при столкновении с почвой его температура по­высилась с 20 о С до 23 о С?Считать, что выделившееся в результате столкновения коли­чество теплоты распределилось между медным шаром и почвой в соотношении 1:2. Со­противлением воздуха пренебречь. С_м = 390 Дж/(кг∙К).

2.32.Внутренняя энергия теплового излучения в замкнутой полости с объемом V определяется выражением U = Vu,где плотность энергии и = аТ 4 (постоянная а > 0), а давление излучения определяется уравнением состояния p = u/3. Найти уравнение адиабатического процесса.

Видео:29. Адиабатический процесс. Уравнение ПуассонаСкачать

Газ Ван-дер-Ваальса

Видео:Урок 194. Уравнение Ван-дер-ВаальсаСкачать

Уравнение состояния ван-дер-ваальсовского газа

Для реальных газов пользоваться результатами теории идеального газа следует с большой осторожностью. Во многих случаях необходимо переходить к более реалистичным моделям. Одной из большого числа таких моделей может служить газ Ван-дер-Ваальса [1] . В этой модели учитываются собственный объем молекул и взаимодействия между ними. В отличие от уравнения Менделеева — Клапейрона pV= RT, справедливого для идеального газа, уравнение газа Ван-дер-Ваальса содержит два новых параметра а и Ь, не входящих в уравнение для идеального газа и учитывающих межмолекулярные взаимодействия (параметр а) и реальный (отличный от нуля) собственный объем (параметр Ь) молекул. Предполагается, что учет взаимодействия между молекулами в уравнении состояния идеального газа сказывается на величине давления р, а учет их объема приведет к уменьшению свободного для движения молекул пространства — объема V, занимаемого газом. Согласно Ван-дер-Ваальсу уравнение состояния одного моль такого газа записывается в виде:

где Ум — молярный объем величины (а/Ум) и Ь описывают отклонения газа от идеальности.

Величина a/V^, по размерности соответствующая давлению, описывает взаимодействие молекул между собой на больших (по сравнению с размерами самих молекул) расстояниях и представляет так называемое добавочное к внешнему «внутреннее давление» газа р. Константа Ъ в выражении (4.162) учитывает суммарный объем всех молекул газа (равна учетверенному объему всех молекул газа).

Рис. 4.24. К определению константы b в уравнении Ван-дер-Ваальса

Действительно, на примере двух молекул (рис. 4.24) можно убедиться, что молекулы (как абсолютно жесткие шары) не могут сблизиться друг с другом на расстояние, меньшее, чем 2г между их центрами,

т.е. область пространства, «выключенная» из общего объема, занимаемого газом в сосуде, которая приходится на две молекулы, имеет объем

В пересчете на одну молекулу это

ее учетверенный объем.

Поэтому (V_M — b) есть доступный для движения молекул объем сосуда. Для произвольного объема Vи массы т газа с молярной массой М уравнение (4.162) имеет вид

Рис. 4.25. Фазовые состояния в изотермах Ван-дер-Ваальса

где v = т/М — число моль газа, а а’= v 2 a и Ь’= vb — константы (поправки) Ван-дер-Ваальса.

Выражение для внутреннего давления газа в (4.162) записано в виде a/Vj, по следующей причине. Как было сказано в подразделе 1.4.4, потенциальная энергия взаимодействия между молекулами в первом приближении хорошо описывается потенциалом Леннард— Джонса (см. рис. 1.32). На сравнительно больших расстояниях этот потенциал может быть представлен в виде зависимости U

ь , где г — расстояние между молекулами. Поскольку сила F взаимодействия между молекулами связана с потенциальной энергией U как F — —grad U(r), то F

—г 7 . Число молекул в объеме сферы радиуса г пропорционально г 3 , поэтому суммарная сила взаимодействия между молекулами пропорциональна it 4 , а дополнительное «давление» (сила, отнесенная к площади, пропорциональной г 2 ) пропорционально г ь (или

1/F 2 ). При малых значениях г проявляется сильное отталкивание между молекулами, которое косвенно учитывается

Уравнение Ван-дер-Ваальса (4.162) может быть переписано в виде полиномиального (вириального) разложения по степеням У_м (или У):

Относительно V_M это уравнение кубическое, поэтому при заданной температуре Т должно иметь либо один вещественный корень, либо три (далее, полагая, что мы по-прежнему имеем дело с одним моль газа, опустим индекс Мв V_M, чтобы не загромождать формулы).

На рисунке 4.25 в координатахp(V) при различных температурах Т приведены изотермы, которые получаются в качестве решений уравнения (4.163).

Как показывает анализ этого уравнения, существует такое значение параметра Т— Г* (критическая температура), которое качественно разделяет различные типы его решений. При Т > Т_к кривые p(V) монотонно спадают с ростом V, что соответствует наличию одного действительного решения (одно пересечение прямой р = const с изотермой p(V)) — каждому значению давления р соответствует только одно значение объема V. Иными словами, при Т > Т_к газ ведет себя примерно как идеальный (точного соответствия нет и оно получается только при Т -> оо, когда энергией взаимодействия между молекулами по сравнению с их кинетической энергией можно пренебречь). При низких температурах, когда Т Т), и при Т=Т_К он стягивается в точку. Огибающая всех отрезков вида MN образует колоколообразную кривую (бинодаль) — пунктирная кривая MKN на рис. 4.25, отделяющую двухфазную область (под колоколом бинодали) от однофазной — пара или жидкости. При Т> Т_к никаким увеличением давления газообразное вещество превратить в жидкость уже нельзя. Этим критерием можно воспользоваться для проведения условного различия между газом и паром: при Т Т_к никаким давлением газ в жидкость перевести нельзя.

В тщательно поставленных экспериментах можно наблюдать так называемые метастабильные состояния, характеризуемые участками МО и NL на изотерме Ван-дер-Ваальса при Т= Т (штрихпунктирная кривая на рис. 4.25). Эти состояния отвечают переохлажденному пару (участок МО) и перегретой жидкости (участок NL). Переохлажденный пар — это такое состояние вещества, когда по своим параметрам оно должно находиться в жидком состоянии, но по своим свойствам продолжает следовать газообразному поведению — стремится, например, расшириться при увеличении объема. И наоборот, перегретая жидкость — такое состояние вещества, когда оно по своим параметрам должно быть паром, но по свойствам остается жидкостью. Оба эти состояния метастабильны (т.е. неустойчивы): при небольшом внешнем воздействии вещество переходят в стабильное однофазное состояние. Участок OL (определенный математически из уравнения Ван-дер- Ваальса) соответствует отрицательному коэффициенту сжатия (с увеличением объема растет и давление!), оно не реализуется в опытах ни при каких условиях.

Константы а и b считаются независящими от температуры и являются, вообще говоря, разными для разных газов. Можно, однако, модифицировать уравнение Ван-дер-Ваальса так, чтобы ему удовлетворяли любые газы, если их состояния описываются уравнением (4.162). Для этого найдем связь между константами а и b и критическими параметрами: р_к, V_Kn Т_к. Из (4.162) для моль реального газа получаем 1 :

Воспользуемся теперь свойствами критической точки. В этой точке величины йр/dVи tfp/dV 2 равны нулю, так эта точка является точкой перегиба. Из этого следует система трех уравнений:

1 Индекс Мпри объеме моль газа опущен для упрощения записи. Здесь и далее константы а и Ь по-прежнему приведены к одному моль газа.

Эти уравнения справедливы для критической точки. Решение их относительно/>*, У_к, Гадает:

Из последнего соотношения в этой группе формул, в частности, следует, что для реальных газов постоянная R оказывается индивидуальной (для каждого газа со своим набором рк, У к, Т_к она своя), и только для идеального или для реального газа вдали от критической температуры (при Т » Т_к) ее можно полагать равной универсальной газовой постоянной R = k_bN_A. Физический смысл указанного различия кроется в процессах кластерообразования, происходящих в реальных газовых системах в докритических состояниях.

Критические параметры и константы Ван-дер-Ваальса для некоторых газов представлены в табл. 4.3.

Критические параметры и константы Ван-дер-Ваальса

📹 Видео

Уравнение состояния идеального газа. 10 класс.Скачать

Уравнение Ван-дер-Ваальса (вывод и применение). By Bogatov N.A.Скачать

Уравнение Ван-дер-Ваальса | Газы.Молекулярно-кинетическая теория | Химия (видео 8)Скачать

Уравнение Ван дер Ваальса. Часть 3. Внутренняя энергия реального газа. Фазовые переходы 1 рода.Скачать

Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать

Реальные газы. Изотермы Эндрюса и Ван-Дер-Ваальса. Метастабильные состоянияСкачать

Урок 195. Изотермы реального газаСкачать

Реальный газ Уравнение Ван-Дер-ВаальсаСкачать

Закон БернуллиСкачать

Урок 2.Уравнение Менделеева-Клапейрона. Решение задач. База. ЕГЭСкачать

Урок 147. Задачи на основное уравнение МКТ идеального газаСкачать

Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Успеть за 300 секунд, #3: Уравнение Клапейрона-МенделееваСкачать

Задачи на уравнение Менделеева-Клапейрона. Ч.1. Краткая теория + решение задачиСкачать