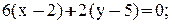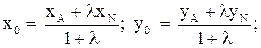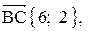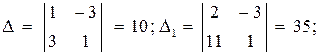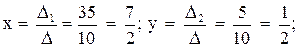Найти длину высоты и написать уравнение перпендикуляра

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

1. Найти уравнение стороны треугольника.
2. Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

Таким образом, уравнение прямой BC —

Угловой коэффициент прямой, перпендикулярной BC,

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

Итак, уравнение высоты, проведённой к стороне BC:

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

Уравнение прямой AB:

Угловой коэффициент перпендикулярной ей прямой

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):

Угловой коэффициент прямой, перпендикулярной AC,

Таким образом, уравнение перпендикулярной AC прямой имеет вид

Подставив в него координаты точки B(5;-3), найдём b:

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

Видео:Уравнение прямой и треугольник. Задача про высотуСкачать

Нужно найти длину высоты AD в треугольнике с вершинами A, B, C и написать уравнение перпендикуляра, опущенного из точки C на прямую AB A( — 3 ; 2), B( — 2 ; — 5), С(6 ; — 1)?

Математика | 10 — 11 классы

Нужно найти длину высоты AD в треугольнике с вершинами A, B, C и написать уравнение перпендикуляра, опущенного из точки C на прямую AB A( — 3 ; 2), B( — 2 ; — 5), С(6 ; — 1).

(x + 2) / 8 = (y + 5) / 4

AD = I — 3 — 4 — 8I / (srqt(1 + 4)) = 15 / sqrt5 = 3 * srqt5

(x + 3) / 1 = (y — 2) / ( — 7)

y + 1 = ( — 1 / 7)(x — 6)

Видео:Вычисляем высоту через координаты вершин 1Скачать

Найти длину перпендикуляра опущенного из начала координат на прямую : (х — 1) / 7 = (у — 1) / 9 = (z — 1) / 11?

Найти длину перпендикуляра опущенного из начала координат на прямую : (х — 1) / 7 = (у — 1) / 9 = (z — 1) / 11.

Видео:Уравнения стороны треугольника и медианыСкачать

Катеты прямоугольного треугольника АВС равны 3см?

Катеты прямоугольного треугольника АВС равны 3см.

Из вершины прямого угла С проведен к плоскости этого треугольника перпендикуляр СД = 1см.

Найти расстояние от точки Д до гипотенузы АВ.

Видео:найти уравнение высоты треугольникаСкачать

Высота и биссектриса прямоугольного треугольника, опущенная из вершины прямого угла, равны, соответственно, 6 и 8?

Высота и биссектриса прямоугольного треугольника, опущенная из вершины прямого угла, равны, соответственно, 6 и 8.

Найдите площадь треугольника.

Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Доказать, что радиус описанной окружности, проведенный в одну из вершин треугольника, перпендикулярен прямой, соединяющей основания высот, проведенных из двух других вершин треугольника?

Доказать, что радиус описанной окружности, проведенный в одну из вершин треугольника, перпендикулярен прямой, соединяющей основания высот, проведенных из двух других вершин треугольника.

Видео:Уравнения прямой на плоскости | Векторная алгебраСкачать

1. Вычислите : 125 в степени 2 / 3 — 0?

1. Вычислите : 125 в степени 2 / 3 — 0.

22. Катет прямоугольного треугольника соответственно равен 12 см.

. Площадь треугольника равна 30 см 2.

Найти длину высоты, опущенной из вершины прямого угла.

23. Основанием прямого конуса является круг с площадью, равной 9 .

Образующая конуса равна 5.

Найти объем конуса 25.

Катеты прямоугольного треугольника соответственно равны 12 см и 5 см.

Найти длину высоты, опущенной из вершины прямого угла11.

Радиус окружности, описанной около прямоугольного треугольника, равен 6 см.

Один катет равен 5 см.

Найти площадь треугольника.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Даны координаты вершины треугольника А(х1 ; у1), В(х2 ; у2), С(х3 ; у3)?

Даны координаты вершины треугольника А(х1 ; у1), В(х2 ; у2), С(х3 ; у3).

Найти : длину стороны АВ ; уравнения сторон треугольника ; внутренний угол при вершине А ; уравнение высоты проведенной через вершину С ; уравнение медианы проведенной через вершину В ; точку пересечения высот ; площадь треугольника АВС.

А( — 4 ; 2) В(0 ; — 1) С(3 ; 3).

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

ПОМОГИТЕЕ ПОЖАЛУЙСТАА В равнобедренном прямоугольном треугольнике с катетами , равными 4 корень из 2, найти высоту опущенную на вершины прямого угла?

ПОМОГИТЕЕ ПОЖАЛУЙСТАА В равнобедренном прямоугольном треугольнике с катетами , равными 4 корень из 2, найти высоту опущенную на вершины прямого угла?

Видео:Как найти длину биссектрисы, медианы и высоты? | Ботай со мной #031 | Борис ТрушинСкачать

Найти высоту, опущенную из вершины равнобедренного треугольника, если угол при вершине равен 2п / 3, а площадь треугольника равна 9корень3?

Найти высоту, опущенную из вершины равнобедренного треугольника, если угол при вершине равен 2п / 3, а площадь треугольника равна 9корень3.

Видео:Аналитическая геометрия на плоскости. Решение задачСкачать

Помогите пожалуйста ?

Точки A(1 ; 4), В( — 2 ; — 2) и С(4 ; 1) являются вершинами треугольника АВС.

Составить уравнение высоты треугольника, опущенной из точки А на сторону ВС.

Определить координаты точки Н — основания высоты АН треугольника АВС.

Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Даны вершины А, В, и С треугольника?

Даны вершины А, В, и С треугольника.

Длину стороны АВ.

2. уравнение сторон АВ и АС.

4. Уравнение высоты СД, опущенной из вершины С и ее длину.

5. Уравнение медианы, проведенной через вершину С.

6. уравнение прямой, проходящей через вершину С параллельно стороне АВ.

Вы открыли страницу вопроса Нужно найти длину высоты AD в треугольнике с вершинами A, B, C и написать уравнение перпендикуляра, опущенного из точки C на прямую AB A( — 3 ; 2), B( — 2 ; — 5), С(6 ; — 1)?. Он относится к категории Математика. Уровень сложности вопроса – для учащихся 10 — 11 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Математика, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

14, 4 * 2 / 3 = 9, 6 км / ч(Скорость 2) 14, 4 + 9, 6 = 24 км / ч(Общая скорость) 42 / 60 = 0, 7 часа 24 * 0, 7 = 16, 8 км (Растояние между деревнями).

V1 = 14, 4км / ч v2 = ? , 2 / 3 t = 42 мин S = ? Решение : V2 = (14, 4 : 3) * 2 = 9, 6км / ч S = t * v S = (42 : 60)•(14, 4 + 9, 6) = 0, 7 + 24 = 24, 7м P. S. надеюсь что так))).

2300 / 4 = 575 575 — 350 = 225.

123456789 * 2007 = 247777775523 123456789 * 2007 = 247777775523 247777775523 — 247777775523 = 1.

400 800 4000 5тон 1 кг 4 тонни 1 кг 3 км 3 км 90 см — 0. 09метрів 100см — 0, 01метрів.

1)35 * 2 = 70(ч) плул катер 2)35 + 3 = 38(км / ч) увеличенная скорость 3)38 * 2 = 76(км) проплыл катер с увеличенной скоростью Ответ : 76 км.

1 2 2 1 10 — 2 + 5 = 13 25 — 25 : 5 = 20 1 2 2 1 18 : 3 • 2 = 12 10 + 3 • 2 = 16 1 1 2 1 25 — 5 • 2 = 15 10 + 10 : 2 = 15 3 1 2 2 1 3 25 — (2 + 3) : 5 = 24 4 • (2 + 3) + 2 = 22 3 2 1 12 + 1 • (3 — 1) = 14.

21 ц = 2100 кг 35 т = 35000 кг 208000 г = 208 кг 90000 г = 90 кг 6 ц = 600 кг 2 т 35 кг = 2035 кг.

(156, 8 — 28, 2) : 2 = 64, 3 64 ; 3 + 28, 2 = 92, 5 64, 3га и 92, 5 га.

1000 метр. Ghastly kink hi David bmp im Tuesday network budget.

Видео:Вычисление медианы, высоты и угла по координатам вершинСкачать

Уравнение высоты треугольника по координатам формула

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

1. Найти уравнение стороны треугольника.
2. Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

Таким образом, уравнение прямой BC —

Угловой коэффициент прямой, перпендикулярной BC,

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

Итак, уравнение высоты, проведённой к стороне BC:

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

Уравнение прямой AB:

Угловой коэффициент перпендикулярной ей прямой

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):

Угловой коэффициент прямой, перпендикулярной AC,

Таким образом, уравнение перпендикулярной AC прямой имеет вид

Подставив в него координаты точки B(5;-3), найдём b:

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

Даны координаты вершин треугольника .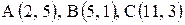

1) Вычислить длину стороны .

2) Составить уравнение линии .

3) Составить уравнение высоты, проведенной из вершины А, и найти ее длину.

4) Найти точку пересечения медиан.

5) Найти косинус внутреннего угла при вершине В.

6) Найти координаты точки М, расположенной симметрично точке А, относительно прямой ВС.

А

1. Длина стороны ВС равна модулю вектора .

; .

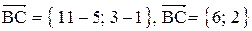
2. Уравнение прямой ВС: ; ; .

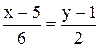
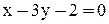
3. Уравнение высоты АК запишем как уравнение прямой, проходящей через точку перпендикулярно вектору :

. Длину высоты АК можно найти как расстояние от точки А до прямой ВС: .

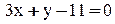
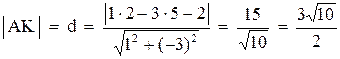
4. Найдем координаты точки N – середины стороны ВС:

; ; .

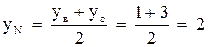
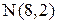
Точка пересечения медиан О делит каждую медиану на отрезки в отношении .

Используем формулы деления отрезка в данном отношении :

.

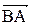
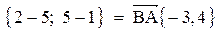
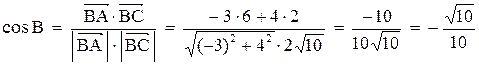
5. Косинус угла при вершине В найдем как косинус угла между векторами и ;

.

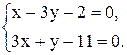
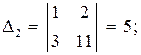
6. Точка М, симметричная точке А относительно прямой ВС, расположена на прямой АК, перпендикулярной к прямой ВС, на таком же расстоянии от прямой, как и точка А. Координаты точки К найдем как решения системы Систему решим по формулам Крамера:

.

Точка К является серединой отрезка АМ.

.

Контрольные варианты к задаче 2

Даны координаты вершин треугольника АВС. Требуется:

1) вычислить длину стороны ВС;

2) составить уравнение линии ВС;

3) составить уравнение высоты, проведенной из вершины А;

4) вычислить длину высоты, проведенной из вершины А;

5) найти точку пересечения медиан;

6) вычислить внутренний угол при вершине В;

7) найти координаты точки М, расположенной симметрично точке А относительно прямой ВС.

1.	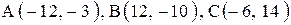.	2.	.
3.	.	4.	.
5.	.	6.	.
7.	.	8.	.
9.	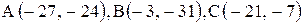.	10.	.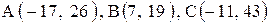
11.	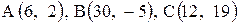.	12.	.
13.	.	14.	.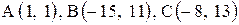
15.	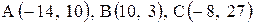.	16.	.
17.	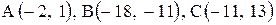.	18.	.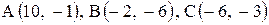
19.	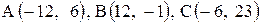.	20.	.
21.	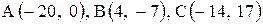.	22.	.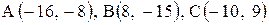
23.	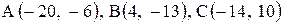.	24.	.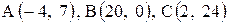
25.	.	26.	.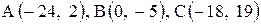
27.	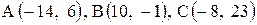.	28.	.
29.	.	30.	.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Учись учиться, не учась! 10637 – | 8008 – или читать все.

Вы можете заказать решение работы
по адресу , вместо бульдога ставьте @

Нужны сторона AB, высота CD, медиана AE и площадь. Координаты вершин А(-8;-3) В(4;-12) С(8;10)

Уравнение прямой, проходящей через две точки (x1,y1) и (x2,y2), описывается уравнением:

Для прямой AB:
(x+8)·(-9)-(y+3)·12 = 0
-9x-72-12y-36 = 0
9x+12y+108 = 0
3x + 4y + 36 = 0

Для отыскания уравнения высоты CD найдем сначала уравнение прямой, которая ей перпендикулярна. Это прямая AB (уравнение у нас есть). Выразим y через x явно:
y = -(3/4)x-9

Если прямая задана уравнением y = kx+b, то перпендикулярная ей прямая будет иметь вид y = (-1/k)x + d. Поэтому искомая высота имеет уравнение:

y = (4/3)x + d. Постоянную d найдем из условия, что высота проходит через точку С.

10 = (32/3) + d,
d = -2/3

Таким образом, уравнение высоты CD: y = (4/3)x – 2/3, или, что то же, 4x-3y-2 = 0

Медиана AE проходит через две точки – точку А и середину отрезка BC. Найдем координаты середины BC по формуле:
X = (x1+x2)/2, Y = (y1+y2)/2. Искомые координаты: X_E = 6, Y_E = -1

Теперь ищем уравнение прямой, идущей через две точки: A(-8;-3) и E(6;-1) по указанному выше уравнению.

(x+8)·2-(y+3)·14 = 0
x+8-7y-21 = 0
x-7y-13 = 0

Это уравнение медианы AE.

Площадь треугольника, заданного на плоскости координатами вершин (x1,y1) (x2,y2) (x3,y3) определяется выражением:

S = (1/2)·|(x3-x1)·(y2-y1) – (y3-y1)·(x2-x1)|
S = (1/2)·|16·(-9)-13·12| = 300/2 = 150 (кв. ед.)

💡 Видео

№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать

Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Расстояние между скрещивающимися прямыми и уравнение их общего перпендикуляра.Скачать

Каноническое уравнение прямой в пространстве Преход от общего уравненияСкачать

12. Уравнения прямой в пространстве Решение задачСкачать

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать

Перпендикуляр и наклонная в пространстве. 10 класс.Скачать