Этот онлайн калькулятор по введенным координатам вершин вычисляет параметры треугольника: длины сторон, углы, периметр и площадь.
Этот онлайн калькулятор предназначен для быстрого вычисления ряда характеристик треугольника по координатам его вершин. Вы вводите координаты вершин A, B и C. Калькулятор рассчитывает по координатам следующие величины:
Обозначения треугольника
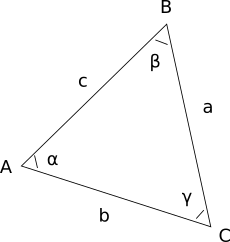
- длину стороны a — стороны, противолежащей вершине А
- длину стороны b — стороны, противолежащей вершине B
- длину стороны c — стороны, противолежащей вершине C
- значение угла α при вершине A
- значение угла β при вершине B
- значение угла γ при вершине C
- периметр треугольника
- площадь треугольника
Если нужно что-то еще, пишите в комментариях, добавим. Формулы расчета значений треугольника описаны под калькулятором.
Видео:Вычисляем высоту через координаты вершин 1Скачать
Решить треугольник Онлайн по координатам
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
| A ( ; ), B ( ; ), C ( ; ) | Примечание: дробные числа записывайте Округлять до -го знака после запятой. Видео:Уравнения стороны треугольника и медианыСкачать  Решение треугольников онлайнС помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже. Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°. Видео:Вычисление медианы, высоты и угла по координатам вершинСкачать  Решение треугольника по трем сторонамПусть известны три стороны треугольника a, b, c (Рис.1). Найдем
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения
Пример 1. Известны стороны треугольника ABC: Решение. Из формул (1) и (2) находим:
И, наконец, находим угол C:
Видео:Уравнения прямой на плоскости | Векторная алгебраСкачать  Решение треугольника по двум сторонам и углу между нимиПусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
Найдем сторону c используя теорему косинусов:
Далее, из формулы
Далее из (3) с помощью калькулятора находим угол A. Поскольку уже нам известны два угла то находим третий:
Пример 2. Известны две стороны треугольника ABC: Решение. Иcпользуя теорму косинусов найдем сторону c:
Из формулы (3) найдем cosA:
Поскольку уже нам известны два угла то находим третий:
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать  Решение треугольника по стороне и любым двум угламПусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
Так как, уже известны два угла, то можно найти третий:
Далее, для находждения сторон b и c воспользуемся тероемой синусов:
Пример 3. Известна одна сторона треугольника ABC: Решение. Поскольку известны два угла, то легко можно найти третий угол С:
Найдем сторону b. Из теоремы синусов имеем:
Найдем сторону с. Из теоремы синусов имеем: 💡 ВидеоУравнение прямой и треугольник. Задача про высотуСкачать  Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать  №973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать  Нахождение стороны прямоугольного треугольникаСкачать  Аналитическая геометрия на плоскости. Решение задачСкачать  Даны координаты вершин треугольника АВС.Скачать  найти уравнение высоты треугольникаСкачать  19. Решение типовых задач по теме "Прямая на плоскости"Скачать  Три точки заданы координатами Найти длину медианы треугольникаСкачать  Задача, которую боятсяСкачать  Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать  Найдите сторону треугольника, если другие его стороны равны 1 и 5Скачать  Аналитическая геометрия, 6 урок, Уравнение прямойСкачать  Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать  Как найти длину биссектрисы, медианы и высоты? | Ботай со мной #031 | Борис ТрушинСкачать  | |||||||||||||||||||||||||||||||||
.
.
Найти 
.
.
, 
.
.
.
.
и 
(Рис.2). Найти сторону c и углы A и B.
.
.
.
.
, 
.
, 
.
и углы 
(Рис.3). Найти стороны b и c и угол С.
