Найдите все значения параметра k при каждом из которых уравнение 1 2 2k sint (6 видео)

Задача 32142 Найдите все значения параметра k при.

Содержание

Условие
Решение
Найдите все k, при каждом из которых уравнений (1 + (2 — 2k)sint) / (cost — sint) = 2k имеет хотя бы одно решение на интервале (0, П / 2)?
Решить уравнение : sint / 1 — cost = 0?
Arccos и решение уравнения cost = a?
А) Sint 4 июл. 2021 г., 04:03:20 | 10 — 11 классы
Значение вырождения (sint — cost) ^ 2 + 2 * sint * cost равно ?
Tgt = — 5 / 12 п / 2Найти sinT cosT ctgT?
Найдите все значения а, при каждом из которых уравнение (2х + 3) + (2х — 3) = ах + 6 имеет ровно два решения?
Найти все а, при каждом из которых хотя бы одно из решений уравнения 3x – 12a = 4ax больше а?
Решите тригонометрическое уравнениеcost = √3 / 2Sint = √3 / 2Tgx = √3?
Найдите все значения параметра , при каждом из которых система уравненийимеет не более двух решений?
Помогите пожалуйста?
Найдите все значения k, при каждом из которых уравнение ((1 + (2-2k)) / (cost — sint)) = 2k имеет хотя бы одно решение на интервале (0; pi / 2).
Ответы
📺 Видео

Условие

Найдите все значения параметра k при каждом из которых уравнение (2(k+1)cost-k)/(sint+cost) = 2 имеет хотя бы одно решение на отрезке [Pi/2; Pi]

Решение

Перепишем уравнение в виде:
2(k+1)cost — k =2sint + 2cost; sint + cost ≠ 1 ⇒ [b]t≠3π/4[/b]

2(k+1)cost — k =2sint + 2cost;

2kcost — k = 2sint

y=2sint/(2cost-1); cost ≠ 1/2

y`> 0 при любом t области определения D(y)

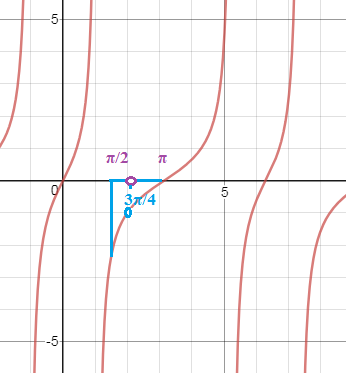
Значит функция строго возрастает на[b][π/2;3π/4)[/b] и на [b](3π/4;π][/b]

имеет ровно одно решение на [π/2;3π/4) U (3π/4;π]

О т в е т. -2 ≤ k

Видео:✓ Параметры с нуля и до ЕГЭ | Задание 17. Профильный уровень | #ТрушинLive #041 | Борис ТрушинСкачать

Найдите все k, при каждом из которых уравнений (1 + (2 — 2k)sint) / (cost — sint) = 2k имеет хотя бы одно решение на интервале (0, П / 2)?

Математика | 10 — 11 классы

Найдите все k, при каждом из которых уравнений (1 + (2 — 2k)sint) / (cost — sint) = 2k имеет хотя бы одно решение на интервале (0, П / 2).

6 будет число фото скинь фоть.

Видео:Найдите все значения а, при каждом из которых система уравнений имеет ровно четыре различных решенияСкачать

Решить уравнение : sint / 1 — cost = 0?

Решить уравнение : sint / 1 — cost = 0.

Видео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Arccos и решение уравнения cost = a?

Arccos и решение уравнения cost = a.

Видео:Задача 17 ЕГЭ профильный. Параметры с нуляСкачать

А) Sint 4 июл. 2021 г., 04:03:20 | 10 — 11 классы

Видео:Параметры, Легко Решаемые Графически | ЕГЭ 2024 по математикеСкачать

Значение вырождения (sint — cost) ^ 2 + 2 * sint * cost равно ?

Значение вырождения (sint — cost) ^ 2 + 2 * sint * cost равно :

Видео:Все уравнения с параметром на РешуЕГЭ. Тотальный разбор 17 номера ЕГЭ по математикеСкачать

Tgt = — 5 / 12 п / 2Найти sinT cosT ctgT?

Tgt = — 5 / 12 п / 2

Найти sinT cosT ctgT.

Видео:5-часовой стрим по ПАРАМЕТРАМ. Вся алгебра для №17 с нуля и до уровня ЕГЭ 2023Скачать

Найдите все значения а, при каждом из которых уравнение (2х + 3) + (2х — 3) = ах + 6 имеет ровно два решения?

Найдите все значения а, при каждом из которых уравнение (2х + 3) + (2х — 3) = ах + 6 имеет ровно два решения.

Видео:РАЗБОР СЛОЖНОГО ЗАДАНИЯ 18, ПАРАМЕТР. ЕГЭ МАТЕМАТИКА с Артуром ШарифовымСкачать

Найти все а, при каждом из которых хотя бы одно из решений уравнения 3x – 12a = 4ax больше а?

Найти все а, при каждом из которых хотя бы одно из решений уравнения 3x – 12a = 4ax больше а.

Видео:Уравнение с параметром #1 ЕГЭ №507224Скачать

Решите тригонометрическое уравнениеcost = √3 / 2Sint = √3 / 2Tgx = √3?

Решите тригонометрическое уравнение

Видео:ЕГЭ №18 по математике. Задача с параметром. Параметры из реального ЕГЭ | TutorOnlineСкачать

Найдите все значения параметра , при каждом из которых система уравненийимеет не более двух решений?

Найдите все значения параметра , при каждом из которых система уравнений

имеет не более двух решений.

Видео:✓ Параметры в ЕГЭ? Это не страшно! | Математика. Задание 17 | #ТрушинLive #036 | Борис ТрушинСкачать

Помогите пожалуйста?

Найдите sint, cost, tgt, ctgt если t = 13 / 6π зариние спасибо огромное.

На странице вопроса Найдите все k, при каждом из которых уравнений (1 + (2 — 2k)sint) / (cost — sint) = 2k имеет хотя бы одно решение на интервале (0, П / 2)? из категории Математика вы найдете ответ для уровня учащихся 10 — 11 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

А) 5 ост 2. Б) 7 ост 1В)7ост4г)5 ост3 Д)71е)93ж)363з)140, и)45к)116л)24 М)16 н)16, о)17.

Деление многочлена на многочлен.

7 / 12 : 49 / 16 = 7 / 12 * 16 / 49 = 1 / 3 * 4 / 7 = 4 / 21.

Ответ 8 ящиков. Потому что если 18 осталось , то отправили получается 72 кг. 72 9 = 8 ящиков.

Видео:ЕГЭ Профиль 17 заданиеСкачать

Найдите все значения k, при каждом из которых уравнение ((1 + (2-2k)) / (cost — sint)) = 2k имеет хотя бы одно решение на интервале (0; pi / 2).

Видео:Профильный ЕГЭ 2023. Задача 17. Параметры. Методы решенияСкачать

Ответы

ну, я вижу, с параллельностью не все гладко

1. важнее всего доказать, что если внутренние накрест лежащие углы равны, то прямые параллельны. то есть обратную теорему. это делается от противного. а имено, предполагается, что две прямые ас и bd пересекают третью прямую в точках а и c, и при этом не параллельны. то есть где то пересекаются, пусть в точке о. образуется треугольник асо. можно построить равный ему треугольник асо1, так, что вершина о1 лежит в другой, нежели точка o, полуплоскости. из равенства этих треугольников следует, что угол оас = угол о1са; угол о1ас = угол оса; и по условию угол оас = угол асd. получается, о, с и о1 лежат на одной прямой, поскольку со1 является продолжением ос. но точно так же можно показать, что и точки о, а и о1 лежат на одной прямой. получилось, что через две точки (точки о и о1) мы провели две разных прямых (одна проходит через а, другая — через с), а это противоречит аксиоме . это доказывает, что если внутренние накрест лежащие углы равны, то прямые параллельны.

отсюда следует, что две прямые, перпендикулярные третьей, параллельны.

2. обратное утверждение, заданное в , доказывается с использованием теоремы пункта 1.

если две прямые параллельны, а внутренние накрест лежащие углы не равны (предположим, что это так), то через точку пересечения первой прямой с секущей проведем прямую так, чтобы внутренний накрест лежащий угол был равен с углом, образованным второй прямой.

но из пункта 1. мы знаем, что построенная прямая параллельна второй прямой. то есть получилось, что через одну точку проходят две прямые, параллельные одной прямой. противоречие, которое доказывает утверждение .

2)75+60=135(руб)-стоимость куклы и книги вместе.

3)135: 3=45(руб)-цена одного альбома.

4)45*2=90(руб)-заплатила за 2альбома.

5)250-(60+75+90)=250-225=25(руб)-осталось у лены после покупки куклы, книги и 2 альбомов.