Алгебра | 5 — 9 классы
Найдите все значения p, при которых квадратное уравнение 3x² — 2x + p = 0 а) не имеет корней б) имеет два различных корня в) имеет решение С ОБЪЯСНЕНИЕМ.
Лови решение в приложении).
- Составьте какое — нибудь квадратное уравнение, которое :а)не имеет корней ;б)имеет два целых корня ;в)имеет два иррациональных корня ;г)имеет один корень ?
- Помогите пожалуйста с алгеброй : )Значит задание такое :Найдите множество значений a, при которых уравнениене имеет корней ;и : )Найдите множество значений k, при которых уравнение имеет 2 корня ;С об?
- При каких значениях а уравнение 3х ^ 2 — 5х + 2а = 0 а) имеет два различных корня б) имеет только положительные корни в) не имеет отрицательных корней?
- При каких значениях параметр P квадратное уравнение а)имеет два различных корня б)имеет один корень в)не имеет корней?
- Найдите значение a, при котором уравнение ax — 3 = 2x — 1 а) не имеет корней б) имеет бесконечно много корней?
- При каких значениях параметра р квадратное уравнение х ^ 2 + 6рх + 9 = 0 а) имеет два различных корня б) имеет один корень в) не имеет корней?
- Составьте какое — нибудь квадратное уравнение, которое а)не имеет корней ; б)имеет два целых корня ; в)имеет два ироциональных корня ; г)имеет один корень?
- Найдите все значения в при которых уравнение имеет ровно 2 различных корня?
- Указать наиболее целое значение параметра а, при котором уравнение имеет два различных корня?
- Найдите все значения а, при каждом из которых уравнение имеет два корня?
- Квадратные уравнения с параметром
- Решение показательных уравнений с параметрами
- 📸 Видео
Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Составьте какое — нибудь квадратное уравнение, которое :а)не имеет корней ;б)имеет два целых корня ;в)имеет два иррациональных корня ;г)имеет один корень ?
Составьте какое — нибудь квадратное уравнение, которое :
а)не имеет корней ;
б)имеет два целых корня ;
в)имеет два иррациональных корня ;
г)имеет один корень ;
Видео:Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать

Помогите пожалуйста с алгеброй : )Значит задание такое :Найдите множество значений a, при которых уравнениене имеет корней ;и : )Найдите множество значений k, при которых уравнение имеет 2 корня ;С об?
Помогите пожалуйста с алгеброй : )
Значит задание такое :
Найдите множество значений a, при которых уравнение
не имеет корней ;
Найдите множество значений k, при которых уравнение имеет 2 корня ;
С объяснениями, пожалуйста : 3.
Видео:№3 Квадратное уравнение 2x^2-3x+8=0 ДискриминантСкачать

При каких значениях а уравнение 3х ^ 2 — 5х + 2а = 0 а) имеет два различных корня б) имеет только положительные корни в) не имеет отрицательных корней?
При каких значениях а уравнение 3х ^ 2 — 5х + 2а = 0 а) имеет два различных корня б) имеет только положительные корни в) не имеет отрицательных корней.
Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

При каких значениях параметр P квадратное уравнение а)имеет два различных корня б)имеет один корень в)не имеет корней?
При каких значениях параметр P квадратное уравнение а)имеет два различных корня б)имеет один корень в)не имеет корней.
Видео:Решаем квадратное уравнение с параметромСкачать

Найдите значение a, при котором уравнение ax — 3 = 2x — 1 а) не имеет корней б) имеет бесконечно много корней?
Найдите значение a, при котором уравнение ax — 3 = 2x — 1 а) не имеет корней б) имеет бесконечно много корней.
Видео:№5 Неполное квадратное уравнение х^2-3x=0 Как разложить на множители Вынести х за скобку Как решитьСкачать

При каких значениях параметра р квадратное уравнение х ^ 2 + 6рх + 9 = 0 а) имеет два различных корня б) имеет один корень в) не имеет корней?
При каких значениях параметра р квадратное уравнение х ^ 2 + 6рх + 9 = 0 а) имеет два различных корня б) имеет один корень в) не имеет корней?
Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Составьте какое — нибудь квадратное уравнение, которое а)не имеет корней ; б)имеет два целых корня ; в)имеет два ироциональных корня ; г)имеет один корень?
Составьте какое — нибудь квадратное уравнение, которое а)не имеет корней ; б)имеет два целых корня ; в)имеет два ироциональных корня ; г)имеет один корень.
Видео:РАЗБИРАЕМ ДИСКРИМИНАНТ ЧАСТЬ I #shorts #математика #егэ #огэ #дискриминантСкачать

Найдите все значения в при которых уравнение имеет ровно 2 различных корня?
Найдите все значения в при которых уравнение имеет ровно 2 различных корня.
Видео:Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Указать наиболее целое значение параметра а, при котором уравнение имеет два различных корня?
Указать наиболее целое значение параметра а, при котором уравнение имеет два различных корня.
Видео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Найдите все значения а, при каждом из которых уравнение имеет два корня?
Найдите все значения а, при каждом из которых уравнение имеет два корня.
Перед вами страница с вопросом Найдите все значения p, при которых квадратное уравнение 3x² — 2x + p = 0 а) не имеет корней б) имеет два различных корня в) имеет решение С ОБЪЯСНЕНИЕМ?, который относится к категории Алгебра. Уровень сложности соответствует учебной программе для учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.
1 ар x 2 ар 1, 9 + x 3 ар 5x x + 5x = 3(1, 9 + x) x + 5x = 5, 7 + 3x 3x = 5, 7 x = 1, 9 (кг) 1 арбуз 2 арбуз — 3, 8 кг 3 арбуз — 5 * 1, 9 = 9, 5 кг.
Видео:Как решать квадратные уравнения без дискриминантаСкачать

Квадратные уравнения с параметром
Задачи с параметрами. Простейшие задачи на квадратный трёхчлен.
Сегодня мы рассмотрим задачи на квадратный трёхчлен, про который, в зависимости от параметра, надо будет что-то выяснить. Это «что-то» может быть самым разнообразным, насколько только хватит фантазии у составителей задачи. Это самый простой тип задач с параметрами. И, если на ЕГЭ вам попалась такая — считайте, что вам повезло!
Но, прежде чем приступать к разбору самих задач, ответьте сами себе на такие простые вопросы:
— Что такое квадратное уравнение, как оно выглядит и как решается?
— Что такое дискриминант и куда его пристроить?
— Что такое теорема Виета и где её можно применить?
Если вы верно отвечаете на эти простые вопросы, то 50% успеха в решении параметрических задач на квадратный трёхчлен вам обеспечены! А остальные 50% — это обычная алгебра и арифметика: раскрытие скобок, приведение подобных, решение уравнений, неравенств и систем и т.д.
Для начала рассмотрим совсем безобидную задачку. Для разминки. 🙂
Пример 1
Приступаем к решению. Во-первых, чтобы в будущем не накосячить в коэффициентах, всегда полезно выписать их отдельно. Прямо в столбик. Вот так:
Да-да! Часть коэффициентов в уравнении (а именно — b и с) зависит от параметра. В этом как раз и состоит вся фишка таких задач. А теперь снова въедливо перечитываем условие. Ключевой зацепкой в формулировке задания являются слова «единственный корень». И когда же квадратное уравнение имеет единственный корень? Подключаем наши теоретические знания о квадратных уравнениях. Только в одном единственном случае — когда его дискриминант равен нулю.
Осталось составить выражение для дискриминанта и приравнять его к нулю. Поехали!
Теперь надо приравнять наш дискриминант к нулю:
Можно, конечно, решать это квадратное уравнение через дискриминант, а можно немного схитрить. На что у нас похожа левая часть, если как следует присмотреться? Она у нас похожа на квадрат разности (a-3) 2 !
Респект внимательным! Верно! Если заменить наше выражение слева на (a-3) 2 , то уравнение будет решаться в уме!
Вот и всё. Это значит, что единственный корень наше квадратное уравнение с параметром будет иметь только в одном единственном случае — когда значение параметра «а» равно тройке.)
Это был разминочный пример. Чтобы общую идею уловить.) Теперь будет задачка посерьёзнее.
Пример 2
Вот такая задачка. Начинаем распутывать. Первым делом выпишем наше квадратное уравнение:
0,5x 2 — 2x + 3a + 1,5 = 0
Самым логичным шагом, было бы умножить обе части на 2. Тогда у нас исчезнут дробные коэффициенты и само уравнение станет посимпатичнее. Умножаем:
Выписываем в столбик наши коэффициенты a, b, c:
Видно, что коэффициенты a и b у нас постоянны, а вот свободный член с зависит от параметра «а»! Который может быть каким угодно — положительным, отрицательным, целым, дробным, иррациональным — всяким!
А теперь, чтобы продвинуться дальше, вновь подключаем наши теоретические познания в области квадратных уравнений и начинаем рассуждать. Примерно так:
«Для того чтобы сумма кубов корней была меньше 28, эти самые корни, во-первых, должны существовать. Сами по себе. В принципе. А корни у квадратного уравнения существуют, тогда и только тогда, когда его дискриминант неотрицательный. Кроме того, в задании говорится о двух различных корнях. Эта фраза означает, что наш дискриминант обязан быть не просто неотрицательным, а строго положительным!»
Если вы рассуждаете таким образом, то вы движетесь правильным курсом! Верно.) Составляем условие положительности для дискриминанта:
Полученное условие говорит нам о том, что два различных корня у нашего уравнения будет не при любых значениях параметра «а», а только при тех, которые меньше одной шестой! Это глобальное требование, которое должно выполняться железно. Неважно, меньше 28 наша сумма кубов корней или больше. Значения параметра «а», большие или равные 1/6, нас заведомо не устроят. Гуд.) Соломки подстелили. Движемся дальше.
Теперь приступаем к загадочной сумме кубов корней. По условию она у нас должна быть меньше 28. Так и пишем:
Значит, для того чтобы ответить на вопрос задачи, нам надо совместно рассмотреть два условия:
А дальше начинаем отдельно работать с этой самой суммой кубов. Есть два способа такой работы: первый способ для трудолюбивых и второй способ — для внимательных.
Способ для трудолюбивых заключается в непосредственном нахождении корней уравнения через параметр. Прямо по общей формуле корней. Вот так:
Теперь составляем нужную нам сумму кубов найденных корней и требуем, чтобы она была меньше 28:
А дальше — обычная алгебра: раскрываем сумму кубов по формуле сокращённого умножения, приводим подобные, сокращаем и т.д. Если бы корни нашего уравнения получились покрасивее, без радикалов, то такой «лобовой» способ был бы неплох. Но проблема в том, что наши корни выглядят немного страшновато. И подставлять их в сумму кубов как-то неохота, да. Поэтому, для того чтобы избежать этой громоздкой процедуры, я предлагаю второй способ — для внимательных.
Для этого раскрываем сумму кубов корней по соответствующей формуле сокращенного умножения. Прямо в общем виде:
А дальше проделываем вот такой красивый фокус: во вторых скобках выражаем сумму квадратов корней через сумму корней и их произведение. Вот так:
Казалось бы, и что из этого? Сейчас интересно будет! Давайте, посмотрим ещё разок на наше уравнение. Как можно внимательнее:
Чему здесь равен коэффициент при x 2 ? Правильно, единичке! А как такое уравнение называется? Правильно, приведённое! А, раз приведённое, то, стало быть, для него справедлива теорема Виета:
Вот и ещё одна теорема нам пригодилась! Теперь, прямо по теореме Виета, подставляем сумму и произведение корней в наше требование для суммы кубов:
Осталось раскрыть скобки и решить простенькое линейное неравенство:
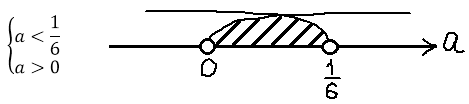
Вспоминаем, что ещё у нас есть глобальное требование a 0 необходимо пересечь с условием a . Рисуем картинку, пересекаем, и записываем окончательный ответ.
Да. Вот такой маленький интервальчик. От нуля до одной шестой… Видите, насколько знание теоремы Виета, порой, облегчает жизнь!
Вот вам небольшой практический совет: если в задании говорится о таких конструкциях, как сумма, произведение, сумма квадратов, сумма кубов корней, то пробуем применить теорему Виета. В 99% случаев решение значительно упрощается.
Это были довольно простые примеры. Чтобы суть уловить. Теперь будут примеры посолиднее.
Например, такая задачка из реального варианта ЕГЭ:
Пример 3
Что, внушает? Ничего не боимся и действуем по нашему излюбленному принципу: «Не знаешь, что нужно, делай что можно!»
Опять аккуратно выписываем все коэффициенты нашего квадратного уравнения:
А теперь вчитываемся в условие задачи и находим слова «модуль разности корней уравнения». Модуль разности нас пока не волнует, а вот слова «корней уравнения» примем во внимание. Раз говорится о корнях (неважно, двух одинаковых или двух различных), то наш дискриминант обязан быть неотрицательным! Так и пишем:
Что ж, аккуратно расписываем наш дискриминант через параметр а:
А теперь решаем квадратное неравенство. По стандартной схеме, через соответствующее квадратное уравнение и схематичный рисунок параболы:
Значит, для того чтобы у нашего уравнения в принципе имелись хоть какие-то корни, параметр а должен находиться в отрезке [-1; 3]. Это железное требование. Хорошо. Запомним.)
А теперь приступаем к этому самому модулю разности корней уравнения. От нас хотят, чтобы вот такая штука
принимала бы наибольшее значение. Для этого, ничего не поделать, но теперь нам всё-таки придётся находить сами корни и составлять их разность: x1 — x2. Теорема Виета здесь в этот раз бессильна.
Что ж, считаем корни по общей формуле:
Дальше составляем модуль разности этих самых корней:
Теперь вспоминаем, что корень квадратный — величина заведомо неотрицательная. Стало быть, без ущерба для здоровья, модуль можно смело опустить. Итого наш модуль разности корней выглядит так:
И эта функция f(a) должна принимать наибольшее значение. А для поиска наибольшего значения у нас есть такой мощный инструмент, как производная! Вперёд и с песнями!)
Дифференцируем нашу функцию и приравниваем производную к нулю:
Получили единственную критическую точку a = 2. Но это ещё не ответ, так как нам ещё надо проверить, что найденная точка и в самом деле является точкой максимума! Для этого исследуем знаки нашей производной слева и справа от двойки. Это легко делается простой подстановкой (например, а = 1,5 и а = 2,5).
Слева от двойки производная положительна, а справа от двойки — отрицательна. Это значит, что наша точка a = 2 и вправду является точкой максимума. Заштрихованная зона на картинке означает, что нашу функцию мы рассматриваем только на отрезке [1; 3]. Вне этого отрезка нашей функции f(a) попросту не существует. Потому, что в заштрихованной области наш дискриминант отрицательный, и разговоры о каких-либо корнях (и о функции тоже) бессмысленны. Это понятно, думаю.
Всё. Вот теперь наша задача полностью решена.
Здесь было применение производной. А бывают и такие задачи, где приходится решать уравнения либо неравенства с так ненавистными многими учениками модулями и сравнивать некрасивые иррациональные числа с корнями. Главное — не бояться! Разберём похожую злую задачку (тоже из ЕГЭ, кстати).
Пример 4
Итак, приступаем. Первым делом замечаем, что параметр а ни в коем случае не может быть равен нулю. Почему? А вы подставьте в исходное уравнение вместо а нолик. Что получится?
Получили линейное уравнение, имеющее единственный корень x=2. А это уже совсем не наш случай. От нас хотят, чтобы уравнение имело два различных корня, а для этого нам необходимо, чтобы оно, как минимум, было хотя бы квадратным.)
При всех остальных значениях параметра наше уравнение будет вполне себе квадратным. И, следовательно, чтобы оно имело два различных корня, необходимо (и достаточно), чтобы его дискриминант был положительным. То есть, первое наше требование будет D > 0.
А далее по накатанной колее. Считаем дискриминант:
D = 4(a-1) 2 — 4a(a-4) = 4a 2 -8a+4-4a 2 +16a = 4+8a
Вот так. Значит, наше уравнение имеет два различных корня тогда и только тогда, когда параметр a > -1/2. При прочих «а» у уравнения будет либо один корень, либо вообще ни одного. Берём на заметку это условие и движемся дальше.
Далее в задаче идёт речь о расстоянии между корнями. Расстояние между корнями, в математическом смысле, означает вот такую величину:
Зачем здесь нужен модуль? А затем, что любое расстояние (что в природе, что в математике) — величина неотрицательная. Причём здесь совершенно неважно, какой именно корень будет стоять в этой разности первым, а какой вторым: модуль — функция чётная и сжигает минус. Точно так же, как и квадрат.
Значит, ответом на вопрос задачи является решение вот такой системы:
Теперь, ясен перец, нам надо найти сами корни. Здесь тоже всё очевидно и прозрачно. Аккуратно подставляем все коэффициенты в нашу общую формулу корней и считаем:
Отлично. Корни получены. Теперь начинаем формировать наше расстояние:
Наше расстояние между корнями должно быть больше трёх, поэтому теперь нам надо решить вот такое неравенство:
Неравенство — не подарок: модуль, корень… Но и мы всё-таки уже решаем серьёзную задачу №18 из ЕГЭ! Делаем всё что можно, чтобы максимально упростить внешний вид неравенства. Мне здесь больше всего не нравится дробь. Поэтому первым делом я избавлюсь от знаменателя, умножив обе части неравенства на |a|. Это можно сделать, поскольку мы, во-первых, в самом начале решения примера договорились, что а ≠ 0, а во-вторых, сам модуль — величина неотрицательная.
Итак, смело умножаем обе части неравенства на положительное число |a|. Знак неравенства сохраняется:
Вот так. Теперь в нашем распоряжении имеется иррациональное неравенство с модулем. Ясное дело, для того чтобы решить его, надо избавляться от модуля. Поэтому придётся разбивать решение на два случая — когда параметр а, стоящий под модулем, положителен и когда отрицателен. Другого пути избавиться от модуля у нас, к сожалению, нет.
Случай 1 (a>0, |a|=a)
В этом случае наш модуль раскрывается с плюсом, и неравенство (уже без модуля!) принимает следующий вид:
Неравенство имеет структуру: «корень больше функции». Такие иррациональные неравенства решаются по следующей стандартной схеме:
Отдельно рассматривается случай а), когда обе части неравенства возводятся в квадрат и правая часть неотрицательна и отдельно — случай б), когда правая часть всё-таки отрицательна, но зато сам корень при этом извлекается.) И решения этих двух систем объединяются.
Тогда, в соответствии с этой схемой, наше неравенство распишется вот так:
А теперь можно существенно упростить себе дальнейшую работу. Для этого вспомним, что в случае 1 мы рассматриваем только a>0. С учётом этого требования, вторую систему можно вообще вычеркнуть из рассмотрения, поскольку, второе неравенство в ней (3a 0 и a
Упрощаем нашу совокупность с учётом главного условия a>0:
Вот так. А теперь решаем самое обычное квадратное неравенство:
Нас интересует промежуток между корнями. Стало быть,
Отлично. Теперь этот промежуток пересекаем со вторым условием системы a>0:
Есть. Таким образом, первым кусочком ответа к нашему неравенству (а пока не ко всей задаче!) будет вот такой интервал:
Всё. Случай 1 разложен по полочкам. Переходим к случаю 2.
Случай 2 (a
В этом случае наш модуль раскрывается с минусом, и неравенство принимает следующий вид:
Опять имеем структуру: «корень больше функции». Применяем нашу стандартную схему с двумя системами (см. выше):
С учётом общего требования a
А дальше снова решаем обычное квадратное неравенство:
И опять сокращаем себе работу. Ибо оно у нас уже решено в процессе разбора случая 1! Решение этого неравенства выглядело вот так:
Осталось лишь пересечь этот интервал с нашим новым условием a
Вот и второй кусочек ответа готов:
Кстати сказать, как я узнал, что ноль лежит именно между нашими иррациональными корнями? Легко! Очевидно, что правый корень заведомо положителен. А что касается левого корня, то я просто в уме сравнил иррациональное число
с нулём. Вот так:
А теперь объединяем оба найденных интервала. Ибо мы решаем совокупность (а не систему):
Готово дело. Эти два интервала — это пока ещё только решение неравенства
Кто забыл, данное неравенство отвечает у нас за расстояние между корнями нашего уравнения. Которое должно больше 3. Но! Это ещё не ответ!
Ещё у нас есть условие положительного дискриминанта! Неравенство a>-1/2, помните? Это значит, что данное множество нам ещё надо пересечь с условием a>-1/2. Иными словами, теперь мы должны пересечь два множества:
Но есть одна проблемка. Мы не знаем, как именно расположено на прямой число -1/2 относительно левого (отрицательного) корня. Для этого нам придётся сравнить между собой два числа:
Поэтому сейчас берём черновик и начинаем сравнивать наши числа. Примерно так:
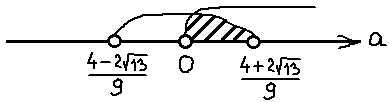
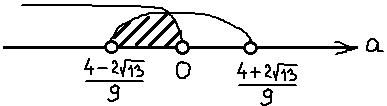
Это значит, что дробь -1/2 на числовой прямой находится левее нашего левого корня. И картинка к окончательному ответу задачи будет какая-то вот такая:
Всё, задача полностью решена и можно записывать окончательный ответ.
Ну как? Уловили суть? Тогда решаем самостоятельно.)
1. Найдите все значения параметра b, при которых уравнение
ax 2 + 3x +5 = 0
имеет единственный корень.
2. Найдите все значения параметра а, при каждом из которых больший корень уравнения
x 2 — (14a-9)x + 49a 2 — 63a + 20 = 0
3. Найдите все значения параметра а, при каждом из которых сумма квадратов корней уравнения
x 2 — 4ax + 5a = 0
4. Найдите все значения параметра а, при каждом из которых уравнение
x 2 + 2(a-2)x + a + 3 = 0
имеет два различных корня, расстояние между которыми больше 3.
Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Решение показательных уравнений с параметрами
Разделы: Математика
Цели урока: Учащиеся должны знать способы решений уравнений вида 
Ход урока.
Для первой группы учащихся выдавались следующие задания.
Для каждого значения a решить уравнения:
Задания для второй группы учащихся.
Указать число решений в зависимости от параметра а.
Третья группа решает уравнения, сводящиеся к квадратным.
Задание 1. Решить уравнение p · 4 x – 4 · 2 x + 1 = 0 и указать число решений в зависимости от параметра p.
Задание 2. При каких a уравнение 9 x + (2a + 4) · 3 x + 8a + 1 = 0 имеет единственное решение.
Задание 3. Указать число решений уравнения 49 x + 2p · 7 x + p 2 – 1 = 0 в зависимости от параметра p.
Задание 4. При каких значениях p уравнение 4 x – (5p – 3) · 2 x + 4p 2 – 3p = 0 имеет единственное решение.
Выступление первой группы – решение показательных уравнений вида
Докладывает лидер первой группы и привлекает к своему докладу участников этой группы. То есть диалог идёт ученик – ученик.
Решение исходного уравнения сводится к решению линейного уравнения с параметрами kx = b.
Если k = 0, b = 0, то 0 · x = 0, – любое действительное число.
Если k = 0, b ≠ 0, то 0 · x = b – нет решений.
Если k ≠ 0, то 
Задание 1. Решить уравнение 
Докладчик решает у доски с комментариями, остальные записывают в тетрадях.
Значит уравнение (1) можно представить в виде (a – 1)(a + 4)x = (a – 1)(a – 1)(a – 3).
Исследуем полученное уравнение:
Ответ:
На этом выступление первой группы закончено. Решение остальных заданий этой группы см. Приложение, стр. 1.
Выступление второй группы – решение уравнений вида
Докладывает лидер второй группы и привлекает к обсуждению этого вопроса всех учащихся. Исходное уравнение равносильно уравнению ax 2 + bx + c1 = c0, или ax 2 + bx + c = 0.
Далее идёт диалог ученик–ученик.
- Какое уравнение получили? – Это уравнение степени не выше второй.
- При a = 0, bx + c = 0, получили линейное уравнение, которое может иметь одно решение, не иметь корней, или иметь бесконечное множество решений.
- При a ≠ 0, ax 2 + bx + c = 0, квадратное уравнение.
- От чего зависит число решений квадратного уравнения? – Число решений квадратного уравнения зависит от дискриминанта. Если D = 0 то квадратное уравнение имеет одно решение. Если D > 0, то два решения. Если D 2 + 2(a + 3)x + a + 2 = 0.
Ответ:
На этом выступление второй группы закончено. Решение остальных заданий этой группы см. Приложение, стр. 2.
Выступление третьей группы – решение уравнений вида af 2 (x) + bf(x) + c = 0, где f(x) – показательная функция. Способ решения – введение новой переменной. f(x) = t, t > 0.
Слово предоставляется выступающему от третьей группы. Он докладывает, что их группа решала уравнения вида: (1) af 2 (x) + bf(x) + c = 0, где f(x) – показательная функция. Способ решения – введение новой переменной. f(x) = t, t > 0.
Исходное уравнение (1) равносильно
Далее докладчик задаёт вопросы, а учащиеся отвечают на них.
При каких условиях уравнение (1) имеет один корень?
- При a = 0 уравнение (2) становится линейным, значит может иметь только один корень, и он должен быть положительным.
- Если D = 0, уравнение (2) имеет один корень, и он должен быть положительным.
- Если D > 0, уравнение (2) имеет два корня, но они должны быть различных знаков.
- Если D > 0, уравнение (2) имеет два корня, но один из низ нуль. А второй положительный.
При каких условиях уравнение (1) имеет два корня?
Исходное уравнение имеет два корня, если уравнение (2) имеет два корня и оба они положительны.
При каких условиях уравнение (1) не имеет корней?
- Если Dx – 4 · 2 x + 1 = 0 и указать число решений в зависимости от параметра p.
Ответим на вопрос: При каких значениях p уравнение (1) имеет один корень?
- Если
одно решение. Обсуждается вопрос какие ещё могли быть варианты при t = 0 – нет решений, при t 0.
Уравнение будет иметь единственное решение при условии. Что дискриминант уравнения (2) есть число положительное, но корни при этом имеют различные знаки. Эти условия достигаются с помощью теоремы Виета. Чтобы корни квадратного трёхчлена были действительными и имели различные знаки, необходимо и достаточно выполнение соотношений.
Итак, уравнение (1) имеет единственное решение при p ≤ 0, p = 4.
Теперь остаётся ответить на вопрос. При каких условиях исходное уравнение (2) имеет два решения? Это возможно, если уравнение (2) имеет два корня и оба они положительны. По теореме Виета для того, чтобы корни квадратного трёхчлена были действительными и при этом оба были положительными, необходимо и достаточно выполнение соотношений.
Исходное уравнение имеет два корня при 0 0, то уравнение (2) имеет корни, но они оба отрицательны.
Итак, D 4. При p > 4 – нет решений. Второе условие равносильно следующим соотношениям.
Значит уравнение (1) не имеет решений при p > 4.
Ответ:
- При p = 4, p ≤ 0 одно решение.
- При 0 4 нет решений.
На этом выступление третьей группы закончено. Решение остальных заданий этой группы см. Приложение, стр. 3.
Домашнее задание.
Задание 1. Найти все значения параметра a, при которых уравнение (a – 3) · 4 x – 8 · 6 x + (a +3) 9 x = 0 не имеет корней.
Задание 2.Указать число решений уравнения p · 2 x + 2 –x – 5 = 0 в зависимости от параметра p.
Задание 3. Выяснить при каких значениях a уравнение 
Задание 4. Найти все значения p при которых уравнение (p – 1) · 4 x – 4 · 2 x + (p + 2) = 0 имеет хотя бы одно решение.
Задание 5. Указать число решений уравнения a · 12 |x| = 2 – 12 –|x| в зависимости от параметра a.
📸 Видео
Математика| Разложение квадратного трехчлена на множители.Скачать

Найдите все значения а, при каждом из которых система уравнений имеет ровно четыре различных решенияСкачать

Как решать квадратные уравнения. 8 класс. Вебинар | МатематикаСкачать

№4 Квадратное уравнение 2x^2-3x=1 ДискриминантСкачать

Как решают уравнения в России и США!?Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Формула корней квадратного уравнения. Алгебра, 8 классСкачать

✓ Параметры с нуля и до ЕГЭ | Задание 17. Профильный уровень | #ТрушинLive #041 | Борис ТрушинСкачать









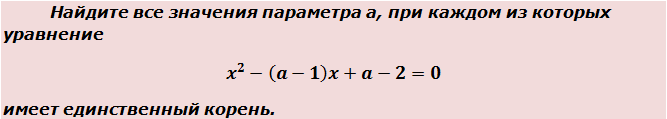
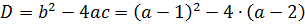
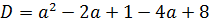
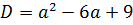
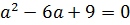
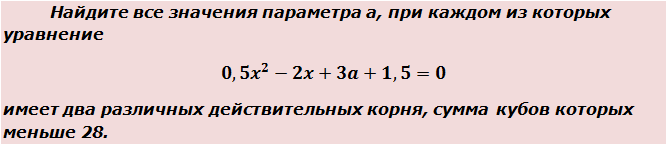
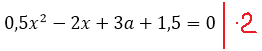
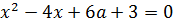
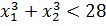
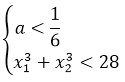
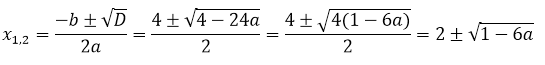
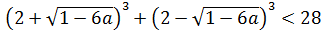
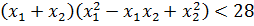
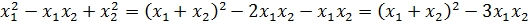
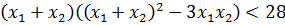
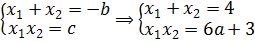
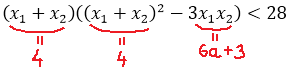
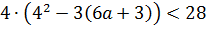
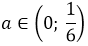
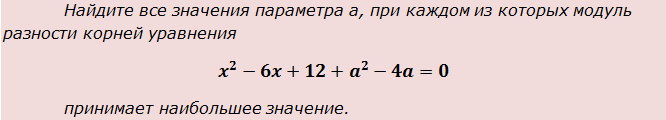
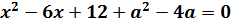
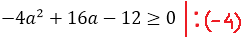
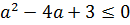
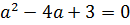
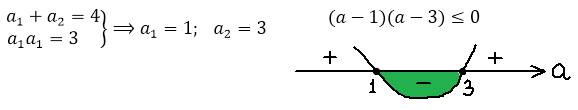
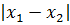
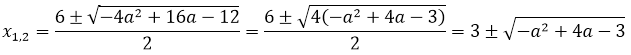
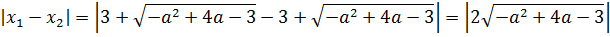
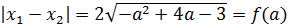
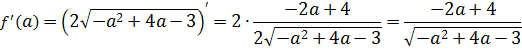
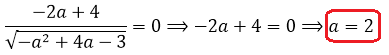
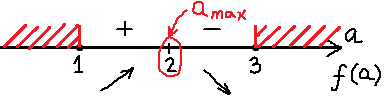
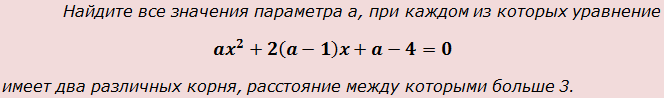
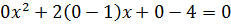
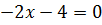
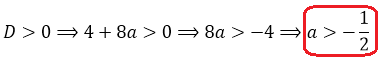
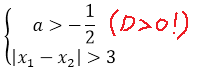
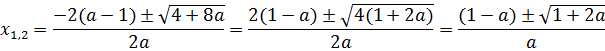
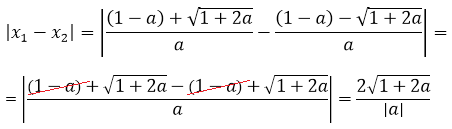
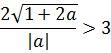
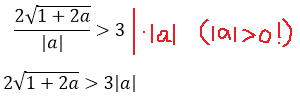
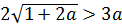
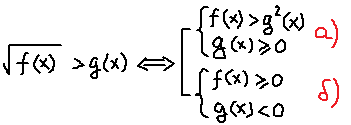
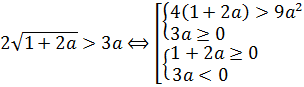
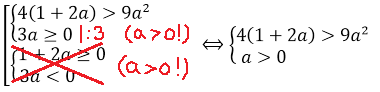
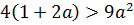
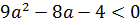
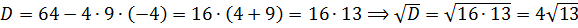
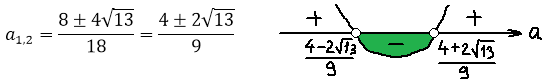
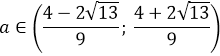
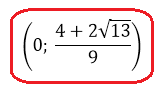
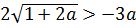
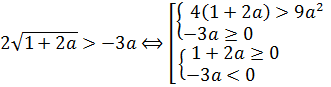
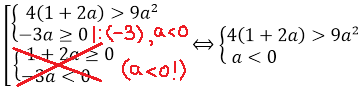
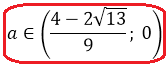
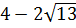
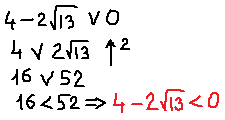
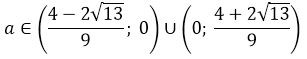
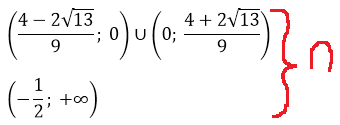
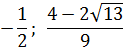
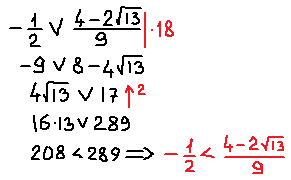
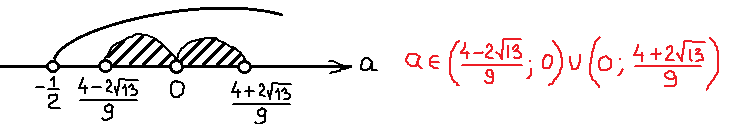











 одно решение. Обсуждается вопрос какие ещё могли быть варианты при t = 0 – нет решений, при t 0.
одно решение. Обсуждается вопрос какие ещё могли быть варианты при t = 0 – нет решений, при t 0.

