Найдите все значения параметра a, при каждом из которых система
имеет единственное решение.
Тогда исходная система равносильна следующей смешанной системе:
Построим её график и определим, при каких значения параметра пучок прямых 
имеет единственную общую точку с объединением двух лучей 
и 
при условиях 
(см. рис.)
Ответ: 
прямая у=5 определена лишь до х=6, значит при больших положительных а будет пересечение лишь с прямой у=х+2, то есть будет одно решение, как нам и нужно. значит в ответе должен быть промежуток от 0 до +беск.
То есть по Вашему после х=6 прямой y=5 нет, а прямая y=x+2 есть?
она есть до х=6 и пересекается с нашей прямой при больших а.
При а>1 пересечений нет
Найдите все значения a, при каждом из которых система
имеет ровно два различных решения.
Решим первое уравнение:
Рассмотрим случай (1): y = −7. При любом a получаем одно решение x = a + 7, для которого неравенство x ≥ −3 верно только при a ≥ −10.
Рассмотрим случай (2):
Так как 
то при 
корней нет, при 
получаем один корень 
при 
получаем два различных корня. У параболы 
— ветви вверх, абсцисса вершины равна 
Значит, оба корня не меньше -3 при 
то есть при 
а при 
один корень меньше −3, а другой — больше −3.
Соберем сведения о числе решений в случаях (1) и (2) в таблице
Остаётся учесть те значения a, при которых решение из случая (1) совпадает с одним из решений случая (2). Тогда 
с учётом 
из 
получаем, что x = 4, a = −3.
Ответ: 
Примечание: для решения задачи можно использовать графо-аналитический метод.
Можете объяснить, как мы из yx^2+y^2-2y-63+7x^2=0 получили (y+7)(y+x^2-9)=0 Всё никак не удаётся преобразовать к такому виду.
Значит, оба корня не меньше -3 при то есть при а при один корень меньше −3, а другой — больше −3.не могу додуматься откуда это -3
Найдите все значения параметра a, при каждом из которых система
имеет ровно 
решений.
Преобразуем систему, получим:
Первое уравнение задает части двух парабол (см. рис.):
Второе уравнение задает окружность радиусом 
с центром 
На рисунке видно, что шесть решений системы получаются, только если окружность проходит через точки 
и 
пересекая параболу еще в четырех точках.
При этом радиус окружности равен 
откуда 
или 
Ответ: 
Найдите все значения параметра a, при каждом из которых система
имеет единственное решение.
Преобразуем исходную систему:
Уравнение 
задает пару пересекающихся прямых 
и 
Система 
задает части этих прямых, расположенные правее прямой 
то есть лучи BD и CE (без точек B и C), см. рис.
Уравнение 
задает прямую m с угловым коэффициентом a, проходящую через точку 
Следует найти все значения a, при каждом из которых прямая m имеет единственную общую точку с объединением лучей BD и 
а) Прямая AB задается уравнением 
Поэтому при 
прямая m не пересечет ни луч BD, ни луч
б) Прямая AC задается уравнением 
Поэтому при 
прямая m пересечет луч BD, но не пересечет луч
в) При 
прямая m пресечет и луч BD, и луч
г) Наконец, при 
прямая m пересечет только луч CE, а при 
она не пересечет ни луч BD, ни луч
Ответ: 
Видео:Математика Найдите все значения a, при каждом из которых система уравнений (x-3)(3x-9-y)=|x-3|^3Скачать
Задача 3596 system<(y^2-xy+3x-y-6)sqrt(x+2)/sqrt(6-x)=0;.
Условие
system Найдите все значения а, при каждом из которых система уравнений имеет ровно два различных решения.
Решение
Ответ: (-6; 1] U U [9; 10)
как получили в первом шаге что y=x-2 и y=3
Решите обычное квадратное уравнение с y^2, и у Вас получатся такие корни
из знаменателя первого уравнения
как получилось, что х=-2
Второй множитель в числителе равен 0
Как получился такой ответ?
Постройте график системы. Постройте график у=-х. Прямая у=а-х параллельна у=-х. Посмотрите, для каких значений а будет только 2 точки пересечения у=а-х с графиком системы.
как получился такой ответ?
почму в ответе -6 не включается ? Ведь она принадлежит x=-2
В этой точке 1 решение
разве 9 должна включаться в итоговый ответ?, там же выколотая точка.
При Х=-2 мы имеем бесконечное число решений, поэтому данную прямую нужно учитывать как ограничение диапазона, но не как часть графика системы. Тогда остаётся две прямые Y=3 и Y=X-2. В этом случае ответ меняется. a принадлежит (1;9)u(9;10). Проверялось на нескольких значениях из предыдущего диапазона.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать
Решение №722 Найдите все значения a, при каждом из которых система уравнений <︃ log3(a − x^2) = log3(a − y^2), x^2 + y^2 = 4x + 6y
Найдите все значения a, при каждом из которых система уравнений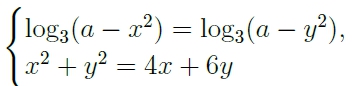
имеет ровно два различных решения.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 3.4 / 5. Количество оценок: 17
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.
Видео:Система уравнений. Метод алгебраического сложенияСкачать
Задание №1221
Видео:Симметрические системы / Как решать по шаблону? x/y+y/x=13/6; x+y=5Скачать
Условие
Найдите все значения a , при каждом из которых система уравнений begin frac<sqrt >=0, \ y=ax end имеет ровно два различных решения.
Видео:Параметры, Легко Решаемые Графически | ЕГЭ 2024 по математикеСкачать
Решение
Решим задачу графически. Построим графики первого и второго уравнения и определим, сколько точек пересечения они имеют при различных значениях параметра.
Первое уравнение frac<sqrt >=0 параметра не содержит и представляет собой равенство дроби нулю. Это выполняется, если числитель равен нулю, а знаменатель не равен нулю, при этом оба выражения имеют смысл.
Запишем уравнение в виде frac<sqrt >=0, разложив числитель на множители. При x leqslant -5 левая часть не имеет смысла. При x>-5 уравнение задаёт прямую y=5 и гиперболу y=frac5x.
Найдём координаты точек A , B и C . B — точка пересечения прямой y=5 и гиперболы y=frac5x , чтобы найти её координаты, нужно решить систему уравнений begin y=5,\y=frac5x. end
У точек A и C абсцисса равна -5, ординаты находим из уравнений прямой и гиперболы. A(-5;5) и C(-5;-1).
При каждом значении a уравнение y=ax задаёт прямую с угловым коэффициентом a , проходящую через начало координат. Чтобы найти значение a , при котором такая прямая проходит через точку с указанными координатами, нужно подставить координаты в уравнение прямой.
Например, для точки A(-5; 5) получаем x=-5, y=5, 5=acdot (-5), a=-1.
Аналогично для B(1;5),, a=5 и для C(-5;-1), a=frac15.
При x>-5 прямая y=ax пересекает прямую y=5 при a и a>0, пересекает правую ветвь гиперболы y=frac5x при a>0, пересекает левую ветвь гиперболы y=frac5x при a>frac15. При этом прямая y=ax проходит через точку пересечения прямой y=5 и гиперболы y=frac5x при a=5.
Число решений исходной системы равно числу точек пересечения прямой y=5 и гиперболы y=frac5x с прямой y=ax при условии x>-5.
Таким образом, исходная система имеет ровно два решения при 0 a=5.
💡 Видео
МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать
Решение систем уравнений методом подстановкиСкачать
Решение систем уравнений. Методом подстановки. Выразить YСкачать
Задача 17 ЕГЭ профильный. Параметры с нуляСкачать
Система НЕЛИНЕЙНЫХ уравнений ★ Как решать ★ Быстрый способ ★ Решите систему x^3+y^3=65; yx^2+xy^2=20Скачать
✓ Параметры с нуля и до ЕГЭ | Задание 17. Профильный уровень | #ТрушинLive #041 | Борис ТрушинСкачать
Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать
Решите систему уравнений: x+y=2 ; xy-z²=1Скачать
Задание 21 ОГЭ по математике #16Скачать
Вариант #10 из задач ФИПИ - Уровень Сложности ЕГЭ 2024| Математика Профиль| Оформление на 100 БалловСкачать
Все уравнения с параметром на РешуЕГЭ. Тотальный разбор 17 номера ЕГЭ по математикеСкачать
Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать
Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать
9 класс, 11 урок, Методы решения систем уравненийСкачать
✓ Пять способов решить задачу с параметром | ЕГЭ-2018. Задание 17. Математика | Борис ТрушинСкачать
