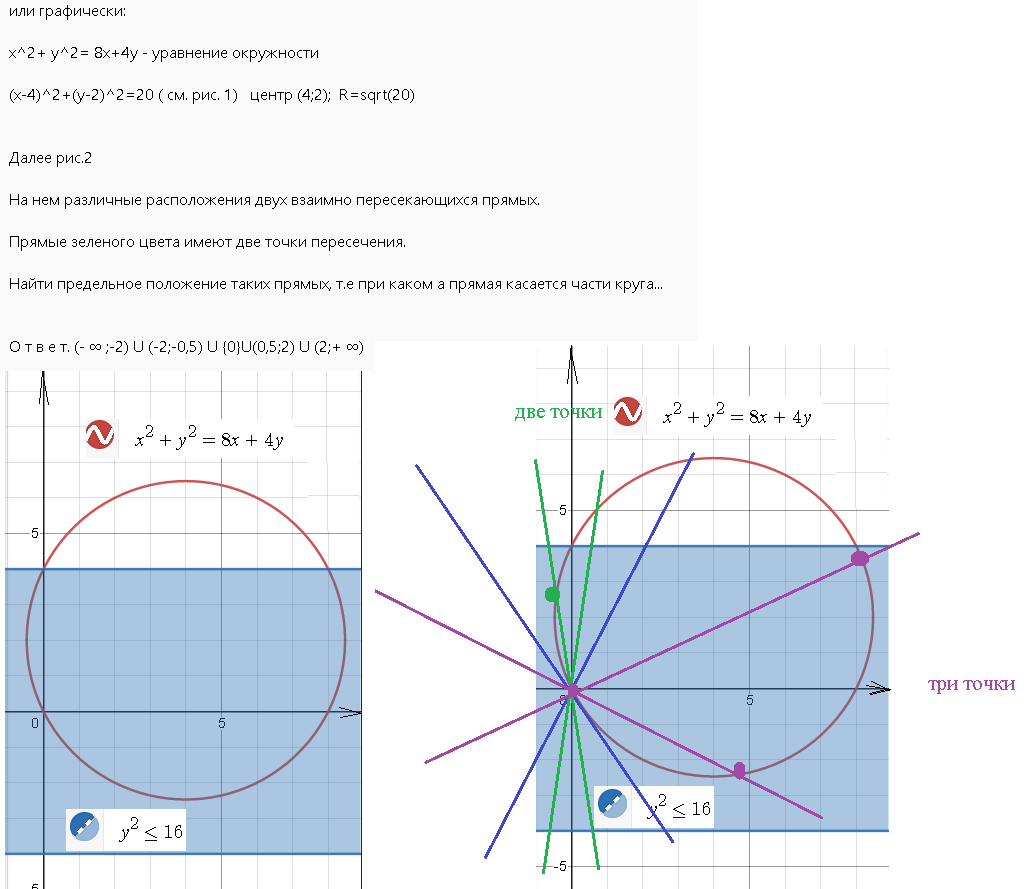
Условие
Найти все значения параметра a, при каждом из которых система уравнений имеет ровно два различных решения
Решение
Первое уравнение определено, если
16-y^2 ≥ 0 ⇒ y^2 ≤ 16 ⇒|y| ≤4 ⇒ [blue][b] -4 ≤ y ≤ 4[/b][/blue]
При [blue][b] -4 ≤ y ≤ 4[/b][/blue] первое уравнение принимает вид:
16-y^2=16-a^2x^2 ⇒ y^2=a^2x^2 ⇒[blue] |y|=|[b]ax[/b]|[/blue] ⇒
Подставляем во второе уравнение:
Совокупность двух систем имеет два решения, если первая система имеет два решения, а вторая не имеет решений или наоборот или
каждая система имеет по одному решению ( отличных одно от другого) 
Видео:№16 Задачи с параметром. ЕГЭ. Задание 18. При каких значениях параметра А система уравнений...Скачать
Решение №722 Найдите все значения a, при каждом из которых система уравнений <︃ log3(a − x^2) = log3(a − y^2), x^2 + y^2 = 4x + 6y
Найдите все значения a, при каждом из которых система уравнений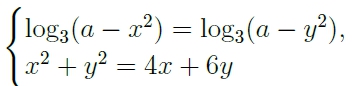
имеет ровно два различных решения.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 3.4 / 5. Количество оценок: 17
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.
Видео:Математика Найдите все значения a, при каждом из которых система уравнений (x-3)(3x-9-y)=|x-3|^3Скачать
Найдите все значения a при каждом из которых система уравнений 16 y2 16 a2x2
Найдите все значения параметра a, при каждом из которых система
имеет единственное решение.
Тогда исходная система равносильна следующей смешанной системе:
Построим её график и определим, при каких значения параметра пучок прямых 
имеет единственную общую точку с объединением двух лучей 
и 
при условиях 
(см. рис.)
Ответ: 
прямая у=5 определена лишь до х=6, значит при больших положительных а будет пересечение лишь с прямой у=х+2, то есть будет одно решение, как нам и нужно. значит в ответе должен быть промежуток от 0 до +беск.
То есть по Вашему после х=6 прямой y=5 нет, а прямая y=x+2 есть?
она есть до х=6 и пересекается с нашей прямой при больших а.
При а>1 пересечений нет
Найдите все значения a, при каждом из которых система
имеет ровно два различных решения.
Решим первое уравнение:
Рассмотрим случай (1): y = −7. При любом a получаем одно решение x = a + 7, для которого неравенство x ≥ −3 верно только при a ≥ −10.
Рассмотрим случай (2):
Так как 
то при 
корней нет, при 
получаем один корень 
при 
получаем два различных корня. У параболы 
— ветви вверх, абсцисса вершины равна 
Значит, оба корня не меньше -3 при 
то есть при 
а при 
один корень меньше −3, а другой — больше −3.
Соберем сведения о числе решений в случаях (1) и (2) в таблице
Остаётся учесть те значения a, при которых решение из случая (1) совпадает с одним из решений случая (2). Тогда 
с учётом 
из 
получаем, что x = 4, a = −3.
Ответ: 
Примечание: для решения задачи можно использовать графо-аналитический метод.
Можете объяснить, как мы из yx^2+y^2-2y-63+7x^2=0 получили (y+7)(y+x^2-9)=0 Всё никак не удаётся преобразовать к такому виду.
Значит, оба корня не меньше -3 при то есть при а при один корень меньше −3, а другой — больше −3.не могу додуматься откуда это -3
Найдите все значения параметра a, при каждом из которых система
имеет ровно 
решений.
Преобразуем систему, получим:
Первое уравнение задает части двух парабол (см. рис.):
Второе уравнение задает окружность радиусом 
с центром 
На рисунке видно, что шесть решений системы получаются, только если окружность проходит через точки 
и 
пересекая параболу еще в четырех точках.
При этом радиус окружности равен 
откуда 
или 
Ответ: 
Найдите все значения параметра a, при каждом из которых система
имеет единственное решение.
Преобразуем исходную систему:
Уравнение 
задает пару пересекающихся прямых 
и 
Система 
задает части этих прямых, расположенные правее прямой 
то есть лучи BD и CE (без точек B и C), см. рис.
Уравнение 
задает прямую m с угловым коэффициентом a, проходящую через точку 
Следует найти все значения a, при каждом из которых прямая m имеет единственную общую точку с объединением лучей BD и 
а) Прямая AB задается уравнением 
Поэтому при 
прямая m не пересечет ни луч BD, ни луч
б) Прямая AC задается уравнением 
Поэтому при 
прямая m пересечет луч BD, но не пересечет луч
в) При 
прямая m пресечет и луч BD, и луч
г) Наконец, при 
прямая m пересечет только луч CE, а при 
она не пересечет ни луч BD, ни луч
Ответ: 
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать
Задание №195
Видео:✓ Параметры с нуля и до ЕГЭ | Задание 17. Профильный уровень | #ТрушинLive #041 | Борис ТрушинСкачать
Условие
Найдите все значения параметра a, при каждом из которых система уравнений имеет более одного решения.
beginx^2+16x+y^2+16y+48=left | x^+y^-16 right |, \ x+y=a end
Видео:Математика | Параметр. Система уравнений с параметромСкачать
Решение
Изобразим на координатной плоскости множество точек, координаты которых удовлетворяют первому уравнению системы.
Рассмотрим два случая:
1) Если x^2+y^2 geqslant 16, получаем уравнение
Это уравнение при соответствующих значениях x и y , удовлетворяющих неравенству x^2+y^2 geqslant 16, задает два луча, выходящих из точек A(-4; 0) и B(0; -4) и расположенных на прямой y=-x-4 .
2) Если x^2+y^2 , то получаем уравнение
Это уравнение при соответствующих значениях x и y , удовлетворяющих неравенству x^2+y^2 задает дугу omega окружности с центром в точке O(-4;-4) и радиусом 4 с концами в точках A и B .
Рассмотрим второе уравнение системы. Оно задает прямую y=-x+a , параллельную прямой АВ или совпадающую с ней при a= -4 (в этом случае система имеет бесконечное множество решений).
Очевидно, что при a система решений иметь не будет.
При a> -4 система уравнений будет иметь более одного решения тогда и только тогда, когда прямая y=-x+a будет пересекать дугу omega в двух различных точках.
Найдем, при каком значении a прямая y=-x+a касается дуги omega . Из соображений симметрии заметим, что касание происходит в точке С с координатами (x_0; y_0) , которая находится на прямой y=x , откуда x_0 = y_0 . Подставляя координаты точки C(x_0; x_0) в уравнение, которое задает дугу omega , имеем:
x_0=2sqrt-4; x_0=-2sqrt -4 не принадлежит дуге omega .
Значит, при -4 система имеет два решения, при a = 4sqrt-8 система имеет одно решение, при a >4sqrt-8 система решений не имеет.
🎦 Видео
Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать
Все уравнения с параметром на РешуЕГЭ. Тотальный разбор 17 номера ЕГЭ по математикеСкачать
ЕГЭ 2018. Задача на параметры. Найдите все значения "a"...Скачать
Найдите все положительные значения параметра а, при каждом из которых система имеет единств решениеСкачать
ЕГЭ 2018 Найдите все значения параметра, при каждом из которых система неравенств имеетСкачать
САМОЕ СЛОЖНОЕ ЗАДАНИЕ 18. ЕГЭ МАТЕМАТИКА, ПАРАМЕТР. АРТУР ШАРИФОВСкачать
Найдите все значения параметра a, при каждом из которых система уравнений имеет ровно два решенияСкачать
Найдите все значения параметра m≦100 , при которых уравнение σ(x)=m имеет решениеСкачать
Задача 17 ЕГЭ профильный. Параметры с нуляСкачать
Найдите все значения параметра а, при которых система имеет единственное решениеСкачать
Решение систем уравнений второго порядка. 8 класс.Скачать
#11. Как решать системы уравнений с параметром графически?Скачать
✓ Система уравнений с параметром | ЕГЭ-2018. Задание 17. Математика. Профиль | Борис ТрушинСкачать
РАЗБОР СЛОЖНОГО ЗАДАНИЯ 18, ПАРАМЕТР. ЕГЭ МАТЕМАТИКА с Артуром ШарифовымСкачать
Решение систем уравнений методом подстановкиСкачать
