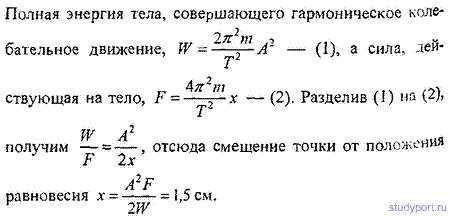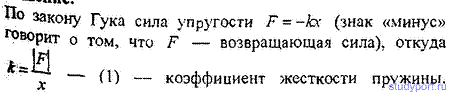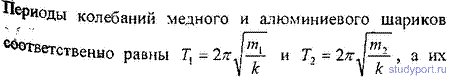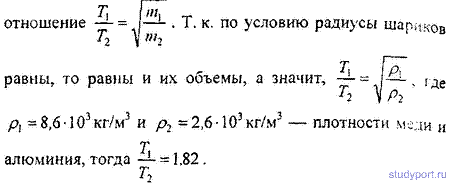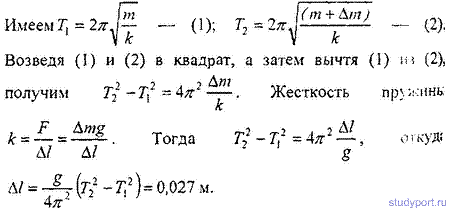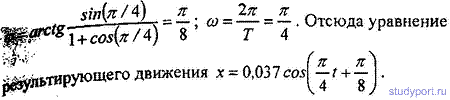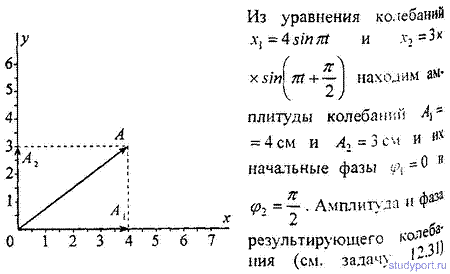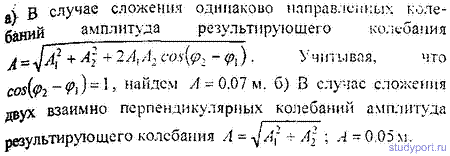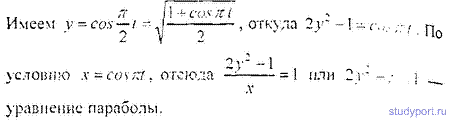Найдите уравнение результирующего колебания полученного от сложения одинаково направленных колебаний (4 видео)

Содержание

Найдите уравнение результирующего колебания полученного от сложения одинаково направленных колебаний
Гармоническое колебательное движение и волны
Сложение взаимно перпендикулярных колебаний
Фигуры Лиссажу
Найдите уравнение результирующего колебания полученного от сложения одинаково направленных колебаний
🎬 Видео

Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Найдите уравнение результирующего колебания полученного от сложения одинаково направленных колебаний

КОЛЕБАНИЯ И ВОЛНЫ

Найти амплитуду А и начальную фазу φ₀ гармоничного колебания, полученного от сложения одинаково направленных колебаний, заданных уравнениями: X = 0,2 sіn (5t + π/2) и X = 0,03 sіn (5t + π//4).

Дано:

Решение:

Амплитуда результирующего колебания

Начальная фаза результирующего колебания

Ответ: ,

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Гармоническое колебательное движение и волны

12.21. Амплитуда гармонических колебаний материальной точки А = 2 см, полная энергия колебаний W = 0,3 мкДж. При каком смещении x от положения равновесия на колеблющуюся точку действует сила F = 22,5 мкН?

12 22. Шарик, подвешенный на нити длиной l = 2 м, отклоняют на угол a = 4° и наблюдают его колебания. Полагая колебаниянезатухающими гармоническими, найти скорость шарика при прохождении им положения равновесия. Проверить полученное решение, найдя скорость шарика при прохождении им положения равновесия из уравнений механики.

12.23. К пружине подвешен груз массой m = 10кг. Зная, что пружина под влиянием силы F = 9,8 Н растягивается на l = 1.5 см, найти период Т вертикальных колебаний груза.

12.24. К пружине подвешен груз. Максимальная кинетическая энергия колебаний груза W_Kma = 1 Дж. Амплитуда колебаний A = 5 см. Найти жесткость к пружины.

12.25. Как изменится период вертикальных колебаний груза, висящего на двух пружинах, если от последовательного соединения пружин перейти к параллельному их соединению?

12.26. Медный шарик, подвешенный к пружине, совершает вертикальные колебания. Как изменится период колебаний, если к пружине подвесить вместо медного шарика алюминиевый такого же радиуса?

12.27. К пружине подвешена чашка весов с гирями. При эгом период вертикальных колебаний T₁ = 0,5 с. После того как на чашку весов положили еще добавочные гири, период вертикальных колебаний стал равным T₂ =0,6 с. На сколько удлинилась пружина от прибавления этого добавочного груза?

12.28. К резиновому шнуру длиной l = 40см и радиусом r = 1мм подвешена гиря массой m = 0,5 кг. Зная, что модуль Юнга резины Е = 3 МН/м 2 , найти период Т вертикальных колебаний гири. Указание: учесть, что жесткость kрезины связана с модулем Юнга Е соотношением к = SE/l, где S — площадь поперечного сечения резины, l — ее длина.

12.29. Ареометр массой m= 0,2 кг плавает в жидкости. Если погрузить его немного в жидкость и отпустить, то он начнет совершать колебания с периодом Т = 3,4 с. Считая колебания незатухающими, найти плотность жидкости p, в которой плавает ареометр. Диаметр вертикальной цилиндрической трубки ареометра d = 1 см.

12.30. Написать уравнение движения, получающегося в результате сложения двух одинаково направленных гармонических колебательных движений с одинаковым периодом T = 8с и одинаковой амплитудой А = 0,02 м. Разность фаз между этими колебаниями φ₂ — φ₁ = P/4 . Начальная фаза одного из этих колебаний равна нулю.

12.31. Найти амплитуду А и начальную фазу φгармонического колебания, полученного от сложения одинаково направленных колебаний, данных уравнениями х₁ = 0,02 х

2.32. В результате сложения двух одинаково направленных гармонических колебаний с одинаковыми амплитудами и одинаковыми периодами получается результирующее колебание с тем же периодом и той же амплитудой. Найти разность фаз φ₂-φ₁ складываемых колебаний.

12.33. Найти амплитуду А и начальную фазу φгармонического колебания, полученного от сложения одинаково направленных колебаний, данных уравнениями x₁ = 4 sinPсм и х₂ = sin(Pt+P/2). Написать уравнение результирующего колебания. Дать векторную диаграмму сложения амплитуд.

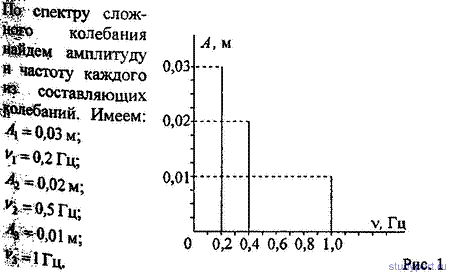
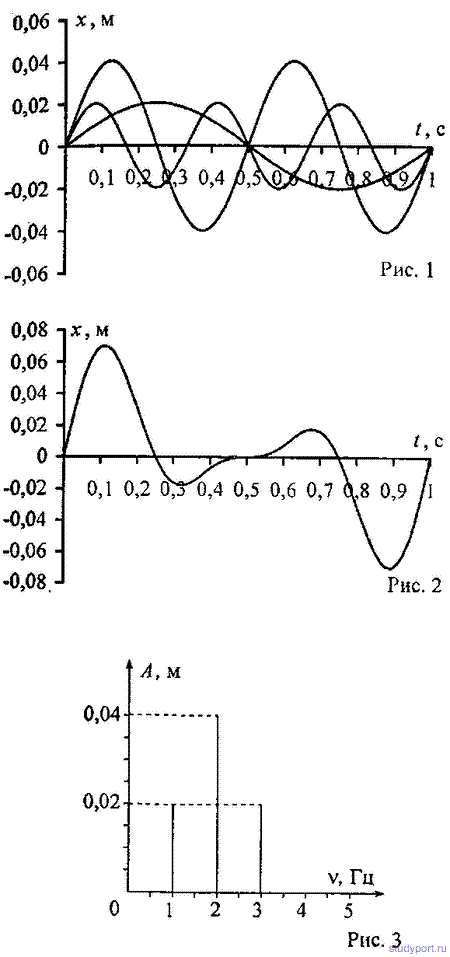
12.34. На рис. 1 дан спектр результирующего колебания. Пользуясь данными этого рисунка, написать уравнения колебаний, из которых составлено результирующее колебание, Начертить график этих колебаний. Принять, что в момент t = 0 разность фаз между этими колебаниями φ₂—φ₁ = 0. Начертить график результирующего колебания.

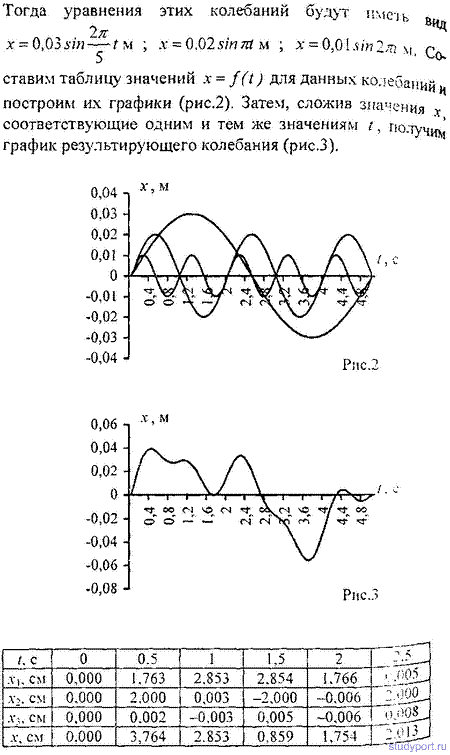
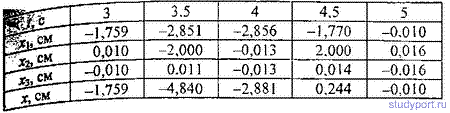
12.35. Уравнения двух гармонических колебаний имеют вид x₁=3sin 4Pt см и х₂ = 6sin10Pt см. Построить график этих колебаний. Сложив графически эти колебания, построить график результирующего колебания. Начертить спектр результирующего колебания.

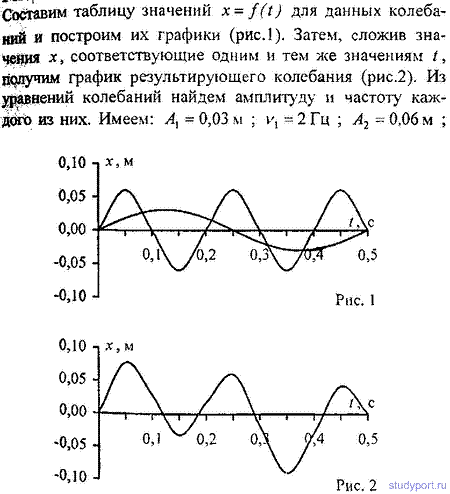
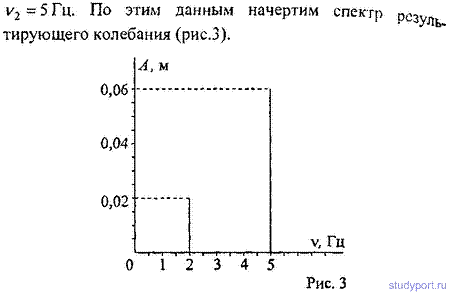
12.36. Уравнение колебаний имеет вид х = Asin2Pv₁t, причем амплитуда А изменяется со временем по закону А = A₀(1 + cos2Pv₂t). Из каких гармонических колебаний состоит колебание? Построить график слагаемых и результирующего колебаний для А₀ = 4 см, v₁ = 2 Гц, v₂ = 1 Гц. Начертить спектр результирующего колебания.

12.37. Написать уравнение результирующего колебания получающегося в результате сложения двух взаимно перпендикулярных колебаний с одинаковой частотой v₁ = v₂ = 5 Гц одинаковой начальной фазой φ₁=φ₂=P/3. Амплитуды колебаний равны A₁ = 0,10 м и А_г = 0,05 м.

12.38. Точка участвует в двух колебаниях одинакового пер» ода с одинаковыми начальными фазами. Амплитуды кол-бан’ 111 равны А, =3см и А, =4 см. Найти амплитуду А р->> льтирУ юшего ко.теоания, если колсоання совершаются: а) в ■ iU -правлении; б) в двух взаимно перпендикулярных паи.:л ; :ях-

12.39. Точка участвует в двух взаимно перпендикулярных колебаниях х = 2sinwt м и у = 2 cos wt м. Найти траекторию результирующего движения точки.

12.40. Точка участвует в двух взаимно перпендикулярных колебания x=cosPtи y = cos P/2 t. Найти траекторию результиующего движения точки и начертить ее с нанесением масштаба.

Ошибка в тексте? Выдели её мышкой и нажми

Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!

Видео:67. Сложение колебанийСкачать

Сложение взаимно перпендикулярных колебаний

Пусть некоторое тело колеблется и вдоль оси х, и вдоль оси у, т.е. участвует в двух взаимно перпендикулярных колебаниях:

Найдем уравнение результирующего колебания. Для простоты примем со, = со₂ = со.

Разность фаз между обоими колебаниями равна Аср = ср₂ — ср,.

Чтобы получить уравнение траектории, надо исключить из этих уравнений время t. Упростим выражения, выбрав начало отсчета так, чтобы ср, = 0, т.е.

В результате решения этих уравнений получим уравнение эллипса, оси которого ориентированы относительнохиу произвольно:

Видео:Гармонические колебанияСкачать

Фигуры Лиссажу

Рассмотрим некоторые частные случаи решений уравнения (2.2.9).

1. Начальные фазы колебаний одинаковы.

Тогда уравнение (2.2.9) примет вид

Это уравнение прямой, проходящей через начало координат (рис. 2.2.5, а). Следовательно, в результате сложения двух взаимно перпендикулярных колебаний с одинаковыми начальными фазами будут происходить колебания вдоль прямой, проходящей через начало координат. Такие колебания называются линейно поляризованными.

2. Начальная разность фаз равна п. Так как cos7t = -l, следовательно, уравнение колебания в этом случае

т.е. точка тоже будет колебаться вдоль прямой, проходящей через начало координат, но прямая лежит в других четвертях по сравнению с первым случаем (рис. 2.2.5, б).

Амплитуда результирующего колебания в обоих случаях

3. Начальная разность фаз равна п/2. Так как sin (к/ 2) = 1, a cos (к/ 2) = = 0, то уравнение (2.2.9) примет вид

Это уравнение эллипса с полуосями А_х и А₂ (рис. 2.2.5, в табл. 2.2.1). В этом случае имеем эллиптически поляризованные колебания.

При А₁ = А₂ получим уравнение окружности (циркулярно-поляризованные колебания).

Рис. 2.2.5. Линейно (а, б) и эллиптически (в) поляризованные колебания

Угол сдвига фаз Дф, град

_ со. Фигуры Лиссажу при — со₂

Найдите уравнение результирующего колебания полученного от сложения одинаково направленных колебаний

4. Все остальные разности фаз дают эллипсы с различным углом наклона относительно осей координат.

Фигуры, получаемые при сложении взаимно перпендикулярных колебаний разных частот, называются фигурами Лиссажу (Ж. Лис- сажу (1822—1880) — французский физик). В простейших случаях можно сравнить частоты по виду фигур.

В приведенных примерах рассматривались простейшие случаи, когда со, = (0₂ = со. Если со, Ф со₂, то в результате будут получаться уже не эллипсы, а более сложные фигуры Лиссажу (см. табл. 2.2.1).

Видео:Урок 338. Сложение колебаний близких частот. БиенияСкачать

Найдите уравнение результирующего колебания полученного от сложения одинаково направленных колебаний

Найти амплитуду А и начальную фазу ф₀ гармонического колебания, полученного от сложения одинаково направленных колебаний, данных уравнениями х₁ = 4 sinПt см и x₂ = 3 sin(Пt+П/2) см. Написать уравнение результирующего колебания и построить векторную диаграмму сложения амплитуд.