| 0. | 0.1. |  – 8 – 8  + 25y = 0; + 25y = 0; | 0.2. |  – 7 – 7  + 12y = – 48sin3x. + 12y = – 48sin3x. |
Решение варианта 0.
Пример 0.1. Характеристическое уравнение 


Пример 0.2. Найдем общее решение соответствующего однородного уравнения 


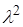




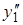
Последнее равенство должно выполнятся для всех x, и это возможно, когда 3A – 21B = 0, 21A + 3B = –48, A = – 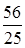

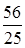



| 1. | 1.1. |  – –  – y = 0; – y = 0; | 1.2. |  – 5 – 5  + 6y = x 2 – x. + 6y = x 2 – x. |
| 2. | 2.1. |  – 2 – 2  + y = 0; + y = 0; | 2.2. |  + +  + y = 3sin2x. + y = 3sin2x. |
| 3. | 3.1. |  + 3 + 3  – 8y = 0; – 8y = 0; | 3.2. |  – –  = x + 1. = x + 1. |
| 4. | 4.1. |  – 4 – 4  + 5y = 0; + 5y = 0; | 4.2. |  + 3 + 3  + 2y = 5e 5x . + 2y = 5e 5x . |
| 5. | 5.1. |  – 2 – 2  + 5y = 0; + 5y = 0; | 5.2. |  + +  – 2y = cosx – 3sinx. – 2y = cosx – 3sinx. |
| 6. | 6.1. | 4  + 4 + 4  + y = 0; + y = 0; | 6.2. |  – 2 – 2  + 10y = 10x 2 + 8x +6. + 10y = 10x 2 + 8x +6. |
| 7. | 7.1. | 9  – –  – 2y = 0; – 2y = 0; | 7.2. |  – 6 – 6  + 25y = 3cosx + 2sinx. + 25y = 3cosx + 2sinx. |
| 8. | 8.1. |  + 3 + 3  = 0; = 0; | 8.2. |  – 5 – 5  = sin5x. = sin5x. |
| 9. | 9.1. |  – –  + 6y = 0; + 6y = 0; | 9.2. |  + 2 + 2  + y = cosx + sinx. + y = cosx + sinx. |
| 10. | 10.1. |  – 5 – 5  + 6y = 0; + 6y = 0; | 10.2. |  – 7 – 7  + 12y = e 3x . + 12y = e 3x . |
| 11. | 11.1. |  + 2 + 2  + y = 0; + y = 0; | 11.2. |  + 2 + 2  + y = 4x 2 – 3x – 5. + y = 4x 2 – 3x – 5. |
| 12. | 12.1. |  – 8 – 8  + 12y = 0; + 12y = 0; | 12.2. |  + y = – sin2x. + y = – sin2x. |
| 13. | 13.1. |  + +  – 6y = 0; – 6y = 0; | 13.2. |  – –  – 2y = 4e 3x . – 2y = 4e 3x . |
| 14. | 14.1. |  – 6 – 6  + 9y = 0; + 9y = 0; | 14.2. |  + 2 + 2  = 4x 3 – 2x. = 4x 3 – 2x. |
| 15. | 15.1. |  + 4 + 4  = 0; = 0; | 15.2. |  + 4 + 4  + 4y = 3cos2x+ 2sin2x. + 4y = 3cos2x+ 2sin2x. |
| 16. | 16.1. |  – 3 – 3  + 2y = 0; + 2y = 0; | 16.2. |  – 4 – 4  + 4y = e 2x . + 4y = e 2x . |
| 17. | 17.1. | 9  + y = 0; + y = 0; | 17.2. |  + 2 + 2  + y = cosx + sinx. + y = cosx + sinx. |
| 18. | 18.1. |  – y = 0; – y = 0; | 18.2. |  – 4 – 4  + 3y = 3e x . + 3y = 3e x . |
| 19. | 19.1. | 2  – 2 – 2  + 3y = 0; + 3y = 0; | 19.2. |  – 6 – 6  + 9y = 5sinx. + 9y = 5sinx. |
| 20. | 20.1. |  + 7 + 7  + 6y = 0; + 6y = 0; | 20.2. |  –3 –3  + 2y = e x . + 2y = e x . |
| 21. | 21.1. |  – 2 – 2  + 19y = 0; + 19y = 0; | 21.2. |  + 2 + 2  + 2y= 2x 3 – 2. + 2y= 2x 3 – 2. |
| 22. | 22.1. |  + +  – 12y = 0; – 12y = 0; | 22.2. |  + 4 + 4  + 5y = 5x 2 – 32x + 5. + 5y = 5x 2 – 32x + 5. |
| 23. | 23.1. | 2  – 3 – 3  – 2y = 0; – 2y = 0; | 23.2. |  – 2 – 2  = x 2 – x. = x 2 – x. |
| 24. | 24.1. |  – 4 – 4  + 7y = 0; + 7y = 0; | 24.2. |  – 3 – 3  – 10y = 3cosx + sinx. – 10y = 3cosx + sinx. |
| 25. | 25.1. |  + 4 + 4  – 7y = 0; – 7y = 0; | 25.2. |  – 4 – 4  +3y= 2x + 1. +3y= 2x + 1. |
Задание 13. Используя дифференциальные уравнения, решить следующие задачи.
Найти семейство функций, таких, что абсцисса точки пересечения касательной к графику каждой из них (в произвольной точке области определения функции) с осью абсцисс равна удвоенной абсциссе точки касания.
Решение варианта 0.
Выберем произвольную функцию искомого семейства и обозначим ее аргумент буквой x, а саму функцию y(x). Пусть (x0,y0) – произвольная точка графика этой функции. Уравнение касательной к графику функции в указанной точке будет иметь вид: y – y0 =k(x – x0), где k = 




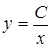
1. Найти кривые, у которых точка пересечения любой касательной с осью абсцисс одинаково удалена от точки касания и от начала координат.
2. Найти кривую, проходящую через точку (0,2), касательные к которой отсекают от оси абсцисс отрезки в два раза большие ординаты точки касания.
3. Найти линии, у которых расстояние любой касательной от начала координат равно абсциссе точки касания.
4. Найти линию, у которой квадрат длины отрезка, отсекаемого любой касательной от оси ординат, равен произведению координат точки касания.
5. Угловой коэффициент касательной к кривой равен ординате точки касания. Найти уравнение кривой, проходящей через точку (0,3).
6. Найти линию, проходящую через точку (1,0) и обладающую тем свойством, что ордината точки пересечения касательной с осью ординат равна удвоенной сумме координат точки касания.
7. Найти кривые, для которых площадь треугольника образованного касательной, прямой, проходящей через точку касания перпендикулярно оси абсцисс и осью абсцисс, есть величина постоянная.
8. Найти кривую, у которой отрезок нормали в любой точке кривой, заключенной между осями координат, делится пополам в этой точке.
9. Найти уравнение кривой, проходящей через точку (3,1), для которой отрезок касательной между точкой касания и осью абсцисс делится пополам в точке пересечения с осью ординат.
10. Найти кривые, у которых точка пересечения любой касательной с осью абсцисс имеет абсциссу вдвое меньше абсциссы точки касания.
11. Определить и построить кривую, проходящую через точку (–2,2), если отрезок AB любой касательной к ней, заключенной между осями координат, делится точкой касания пополам.
12. Определить кривую, проходящую через точку (–1,1), если угловой коэффициент касательной в любой точке кривой равен квадрату ординаты точки касания.
13. Найти уравнение кривой, проходящей через точку (4,3) и обладающую тем свойством, что длина отрезка нормали от точки кривой до точки пересечения с осью ординат равна 5.
14. Найти линию, проходящую через точку (–1,–1), для которой отрезок, отсекаемый касательной к кривой в любой ее точке на оси абсцисс, равен квадрату точки касания.
15. Найти семейство линий, касательные к которым отсекают от оси абсцисс отрезки, равные ординате точки касания.
16. Найти линию, проходящую через точку (0,2), для которой угловой коэффициент касательной в каждой точке линии равен сумме абсциссы и ординаты точки касания.
17. Найти линию, проходящую через точку (2,0) и обладающую тем свойством, что отрезок касательной между точкой касания и осью ординат имеет постоянную длину, равную двум.
18. Найти линию, у которой площадь прямоугольника, построенного на абсциссе любой точки и начальной ординате касательной в этой точке, равна a 2 .
19. Тело движется со скоростью v, пропорциональной квадрату времени. Установить зависимость между пройденным путем s и временем t, если известно, что при t=0, s=s0.
20. Найти линию, проходящую через точку (3,4), у которой отрезок касательной, заключенный между осями координат, делится пополам в точке касания.
21. Определить путь s, пройденный телом за время t, если известно, что скорость в каждый момент времени пропорциональна пройденному пути. Тело проходит 30 м за 1 мин., а 90 м — за 2 мин.
22. За какое время тело, нагретое до 100 0 , охладится до 25 0 , в комнате с t=20 0 , если до 60 0 оно охлаждается за 10 мин? (По закону Ньютона скорость охлаждения тела пропорциональна разности между температурой тела и температурой среды).
23. Найти линию, проходящую через точку (1,–2), для которой отрезок касательной между точкой касания и осью абсцисс делится пополам в точке пересечения с осью ординат.
24. Тело движется по прямой так, что его скорость в каждый момент времени равна корню квадратному из пути, пройденному телом к этому моменту. Найти путь, пройденный телом до момента 10с, если до начала отсчета оно прошло путь 1 м.
25. Найти линию, проходящую через точку (1,1), для которой угловой коэффициент касательной в каждой точке линии обратно пропорционален корню квадратному из ординаты точки касания.
Видео:Математика без Ху!ни. Уравнение касательной.Скачать

IV. Составить дифференциальное уравнение и найти решение.
Для составления ДУ необходимо вспомнить, в чем состоит геометрический и физический смысл производной.
В физических задачах надо прежде всего решить, какую из величин взять за независимую переменную, а какую – за искомую функцию. Затем надо выразить, на сколько изменится искомая функция у, когда независимое переменное х получит приращение 


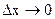

Чтобы решить геометрическую задачу, надо построить чертеж, обозначить искомую кривую через у. Тогда у / — угловой коэффициент касательной, проведенной к искомой кривой. далее надо выразить все упомянутые величины через х, у, у / . Тогда данное в условии задачи соотношение превращается в ДУ, из которого можно найти искомую функцию у(х).
В некоторых задачах содержатся условия, с помощью которых можно определить значения постоянных, входящих в общее решение ДУ.
Примеры
Задача 1. За какое время тело, нагретое до 100 о , охладится до 25 о в комнате с температурой 20 о , если до 60 о оно охладилось за 20 мин. (По закону Ньютона скорость охлаждения тела в воздухе пропорциональна разности температуры воздуха).
Решение. Пусть в момент времени t после начала охлаждения тела его температура будет Т о , тогда, с одной стороны, скорость изменения температуры тела выразится формулой 

Сравнивая оба полученных выражения для скорости изменения температуры, получим:
(знак минус, т.к. как температура тела уменьшается). Получили ДУ первого порядка с разделяющимися переменными. Решая его, получим общее решение:
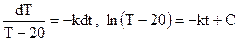
Произвольную постоянную С и коэффициент k можно найти из начальных условий. Подставляя в (*) t=0 мин., Т=100 о , получим 
При t=20 мин., Т=60 о , следовательно:
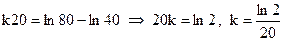
Таким образом, частное решение ДУ, удовлетворяющее всем условиям задачи, будет 

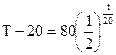
Теперь выясним, через сколько времени температура тела станет раной 25 о . Подставляя вместо Т число 25, находим t:

Следовательно, тело остынет до температуры 25 о через 80 мин.
Задача 2. Найти: 1) семейство кривых, для которых угловой коэффициент касательной равен ординате точки касания; 2) кривую этого семейства, проходящую через точку
Решение. ДУ искомого семейства у / =у или 




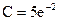
Следовательно, 
Пример 3.Найти кривые, проходящие через точку N(0, 1), для которых площадь треугольника, образованного касательной, ординатой точки касания и осью абсцисс, есть величина постоянная, равная 
Решение. Пусть точка М с координатами (х, у) принадлежит искомой кривой (рис. 1). Тогда МА – отрезок касательной к кривой , причем 
|






Это дифференциальное уравнение с разделяющимися переменными. Решая его, получим:

Учитывая, что кривые проходят через точку N(0, 1), найдем величину С:


Следовательно, уравнения искомых кривых имеет вид

Задание №5 для контрольной работы.
5.1. Найти кривую, проходящую через точку (4, 4), для которой угловой коэффициент касательной в любой точке кривой равен квадрату ординаты точки касания.
5.2. Найти уравнение кривой, для которой отрезок касательной между точкой касания и осью ОХ делится пополам в точке пересечения с осью ОY. Известно, что искомая кривая проходит через точку Р(1, 2).
5.3. Найти линию, проходящую через точку Мо(6, 4) и обладающую тем свойством, что в любой ее точке М нормальный вектор 
5.4. Найти линию, проходящую через точку Мо(1, 1), если отрезок любой ее нормали, заключенный между осями координат, делится точкой линии в соотношении 1:2 (считая от оси OY).
5.5. Найти линию, проходящую через точку Мо(2, -1), если отрезок любой ее касательной между точкой касания и осью ОY делится в точке пересечения с осью абсцисс в соотношении 1:1.
5.6. Найти линию, проходящую через точку Мо(1, 2), если отрезок любой ее касательной, заключенной между осями координат, делится в точке касания в соотношении 1:1.
5.7. Найти линию, проходящую через точку Мо(2, е) и обладающую тем свойством, что в любой ее точке М касательный вектор 
5.8. Найти кривую, проходящую через точку Мо(4, 3), у которой подкасательная есть среднее арифметическое координат точек касания М (подкасательная ТР, где точка Р – проекция точки М на ось ОХ, точка Т – точка пересечения касательной с осью ОХ).
5.9. Найти линию, проходящую через точку Мо(1, 1) и обладающую тем свойством, что в любой ее точке М касательный вектор 
5.10. Найти кривую, для которой сумма длин отрезка касательной к подкасательной пропорциональна произведению координат точки касания М. Кривая проходит через точку Мо(1, 1), коэффициент пропорциональности 
5.11. Пользуясь прямоугольными координатами, найти форму зеркала, собирающего все параллельные лучи в одну точку. Взять падающие лучи параллельными оси ОХ.
5.12. Составит уравнение кривой, проходящей через точку Мо(а, а) и обладающей следующим свойством: если в любой точке М(х, у) кривой с ординатой РМ провести касательную до пересечения с осью ОY в точке Т, то площадь трапеции ОТМР равна 
5.13. Площадь треугольника, образованного радиус-вектором ОМ любой точки М(х, у) кривой, касательной МР к этой точке и осью ОХ, равна 2. Кривая проходит через точку Мо(2, -2). Найти уравнение этой кривой.
5.14. Составить уравнение кривой, проходящей через начало координат, зная, что середина отрезка ее нормали от любой точки кривой М до оси ОХ находится на параболе 
5.15. Определить кривую, проходящую через точку Мо(1, 1), у которой отрезок касательной от точки касания М до пересечения с осью ОХ равен отрезку ОТ, где точка Т – точка пересечения касательной с осью ОХ.
5.16. Найти уравнение кривой, проходящей через точку Мо(1, 1) и обладающей тем свойством, что отрезок, отсекаемый касательной на оси ординат равен квадрату абсциссы точки касания.
5.17. Найти кривую, проходящую через точку Мо(3, 0), у которой отрезок, отсекаемый касательной на оси ординат, равен полусумме координат точки касания.
5.18. Найти кривую, проходящую через точку Мо(1, 1) и обладающую тем свойством, что величина перпендикуляра, опущенного из начала координат на касательную, равна абсциссе точки касания.
5.19. Найти кривую, проходящую через точку Мо(1, 1) и обладающую тем свойством, что отрезок, который касательная в любой точке кривой отсекает на оси ОY равна квадрату абсциссы точки касания.
5.20. Определить кривую, проходящую через точку Мо(0, 1), у которой отношение отрезка, отсекаемого касательной на оси ОY, к радиус-вектору равна 1.
5.21. Найти кривую, у которой подкасательная имеет постоянную длину а. Кривая проходит через точку Мо(а, е) (подкасательная ТР, где точка Р – проекция точки М на ось ОХ, точка Т – точка пересечения касательной с осью абсцисс).
5.22. Найти кривую, проходящую через точку Мо(2, 1), для которой подкасательная равна среднему арифметическому координат точки касания.
5.23. Найти уравнение кривой, проходящей через точку Мо(3, 5) и обладающую тем свойством, что в любой точке М нормальный вектор 
5.24. Найти кривую, проходящую через точку Мо(1, 4) и обладающую тем свойством, что в любой ее точке М касательный вектор 
Раздел 6
КРАТНЫЕ ИНТЕГРАЛЫ
1. Двойной интеграл
1.1. Задача об объеме цилиндрического тела.
1.2. Двойной интеграл и его основные свойства.
1.3. Вычисление двойных интегралов в декартовых координатах.
1.4. Замена переменных в двойном интеграле. Переход от декартовых координат к полярным.
1.5. Приложение двойного интеграла для решения задач геометрии и физики.
Литература 
Вопросы для самопроверки
1. Что называется двойным интегралом от функции f(x; y) по области D? Укажите его геометрический смысл.
2. Сформулируйте теоремы о двойном интеграле от суммы и вынесении постоянного множителя за знак двойного интеграла. Докажите, что

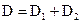
3. Что называется двукратным интегралом от функции f(x; y) по области D? Как он вычисляется?
4. Докажите теорему о среднем для двойного интеграла, укажите ее геометрический смысл.
5. Выведите формулу для вычисления двойного интеграла с помощью двукратного. Дайте геометрическое толкование формулы в случае неотрицательной подынтегральной функции.
6. Обоснуйте формулы, служащие для вычисления объема цилиндрического тела и площади плоской фигуры с помощью двойных интегралов.
7. Выведите формулу для вычисления двойного интеграла в полярных координатах.
8. Каков геометрический смысл интеграла

где z=z(x; y) – функция, обладающая непрерывными частными производными в области D?
9. Каков механический смысл интеграла

где 
10. Выведите формулу для вычисления координат центра тяжести плоской фигуры D, поверхностная плотность которой 
Тройной интеграл
2.1. Тройной интеграл и его основные свойства.
2.2. Вычисление тройных интегралов в декартовых координатах.
2.3. Замена переменных в тройном интеграле. Использование цилиндрических и сферических координат.
2.4. Геометрические и механические приложения тройных интегралов.
Литература 
Вопросы для самопроверки
1. Что называется тройным интегралом от функции f(x, y, z) пространственной области V? Укажите его механический смысл.
2. Что называется трехкратным интегралом от функции f(x, y, z) по области V? Как он вычисляется?
3. Сформулируйте теорему о среднем для тройного интеграла.
4. Выведите формулу для вычисления тройного интеграла с помощью трехкратного. Напишите формулу для вычисления тройного интеграла в цилиндрических координатах.
5. Обоснуйте формулу, служащую для вычисления объема тела с помощью тройного интеграла.
6. Каков механический смысл интеграла

где 

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Уравнение касательной к графику функции
п.1. Уравнение касательной
Рассмотрим кривую (y=f(x)).
Выберем на ней точку A с координатами ((x_0,y_0)), проведем касательную AB в этой точке.
Как было показано в §42 данного справочника, угловой коэффициент касательной равен производной от функции f в точке (x_0): $$ k=f'(x_0) $$ Уравнение прямой AB, проведенной через две точки: ((y_B-y_A)=k(x_B-x_A)).
Для (A(x_0,y_0), B(x,y)) получаем: begin (y-y_0)=k(x-x_0)\ y=k(x-x_0)+y_0\ y=f'(x_0)(x-x_0)+f(x_0) end
Чтобы записать уравнение касательной с угловым коэффициентом в виде (y=kx+b), нужно раскрыть скобки и привести подобные: $$ y=f'(x_0)(x-x_0)+f(x_0)=underbrace_x+underbrace_ $$
п.2. Алгоритм построения касательной
На входе: уравнение кривой (y=f(x)), абсцисса точки касания (x_0).
Шаг 1. Найти значение функции в точке касания (f(x_0))
Шаг 2. Найти общее уравнение производной (f’ (x))
Шаг 3. Найти значение производной в точке касания (f'(x_0 ))
Шаг 4. Записать уравнение касательной (y=f’ (x_0)(x-x_0)+f(x_0)), привести его к виду (y=kx+b)
На выходе: уравнение касательной в виде (y=kx+b)
 | Пусть (f(x)=x^2+3). Найдем касательную к этой параболе в точке (x_0=1). |
(f(x_0)=1^2+3=4 )
(f'(x)=2x )
(f'(x_0)=2cdot 1=2)
Уравнение касательной: $$ y=2(x-1)+4=2x-2+4=2x+2 $$ Ответ: (y=2x+2)
п.3. Вертикальная касательная
Не путайте вертикальные касательные с вертикальными асимптотами.
Вертикальная асимптота проходит через точку разрыва 2-го рода (x_0notin D), в которой функция не определена и производная не существует. График функции приближается к асимптоте на бесконечности, но у них никогда не бывает общих точек.
А вертикальная касательная проходит через точку (x_0in D), входящую в область определения. График функции и касательная имеют одну общую точку ((x_0,y_0)).
Вертикальные касательные характерны для радикалов вида (y=sqrt[n]).
 | Пусть (f(x)=sqrt[5]+1). Найдем касательную к этой кривой в точке (x_0=1). |
(f(x_0)=sqrt[5]+1=1)
(f'(x)=frac15(x-1)^+0=frac15(x-1)^=frac<5(x-1)^> )
(f'(x_0)=frac<5(1-1)^>=frac10=+infty)
В точке (x_0) проходит вертикальная касательная.
Её уравнение: (x=1)
Ответ: (y=2x+2)
п.4. Примеры
Пример 1. Для функции (f(x)=2x^2+4x)
a) напишите уравнения касательных, проведенных к графику функции в точках его пересечения с осью OX.
 | Находим точки пересечения, решаем уравнение: $$ 2x^2+4x=0Rightarrow 2x(x+2)=0Rightarrow left[ begin x=0\ x=-2 end right. $$ Две точки на оси: (0;0) и (-2;0). Касательная в точке (x_0=0): begin f(x_0)=0, f'(x)=4x+4\ f'(x_0)=4cdot 0+4=4\ y=4(x-0)+0=4x end Касательная в точке (x_0=-2): begin f(x_0)=0, f'(x)=4x+4\ f'(x_0)=4cdot (-2)+4=-4\ y=-4(x+2)+0=-4x-8 end |
б) Найдите, в какой точке касательная образует с положительным направлением оси OX угол 45°. Напишите уравнение этой касательной.
 | Общее уравнение касательной: (f'(x)=4x+4) По условию (f'(x_0)=tgalpha=tg45^circ=1) Решаем уравнение: $$ 4x_0+4=1Rightarrow 4x_0=-3Rightarrow x_0=-frac34 $$ Точка касания (x_0=-frac34) begin f(x_0)=2cdotleft(-frac34right)^2+4cdotleft(-frac34right)=frac98-3=-frac end Уравнение касательной: begin y=1cdotleft(x+frac34right)-frac=x-frac98 end |
в) найдите, в какой точке касательная будет параллельна прямой (2x+y-6=0). Напишите уравнение этой касательной.
 | Найдем угловой коэффициент заданной прямой: (y=-2x+6Rightarrow k=-2). Касательная должна быть параллельной, значит, её угловой коэффициент тоже (k=-2). Получаем уравнение: begin f'(x_0)=-2\ 4x_0+4=-2Rightarrow 4x_0=-6Rightarrow x_0=-frac32 end Точка касания (x_0=-frac32) begin f(x_0)=2cdotleft(-frac32right)^2+4cdotleft(-frac32right)=\ =frac92-6=-frac32 end Уравнение касательной: begin y=-2cdotleft(x+frac32right)-frac32=-2x-frac92 end Или, в каноническом виде: begin 2x+y+frac92=0 end |
г) в какой точке функции можно провести горизонтальную касательную? Напишите уравнение этой касательной.
 | У горизонтальной прямой (k=0). Получаем уравнение: (f'(x_0)=0). begin 4x_0+4=0Rightarrow 4x_0=-4Rightarrow x_0=-1 end Точка касания (x_0=-1) begin f(x_0)=2cdot(-1)^2+4cdot(-1)=-2 end Уравнение касательной: begin y=0cdot(x+1)-2=-2 end |
Ответ: а) (y=4x) и (y=-4x-8); б) (y=x-frac98); в) (2x+y+frac92=0); г) (y=-2)
Пример 3*. Найдите точку, в которой касательная к графику функции (f(x)=frac-x) перпендикулярна прямой (y=11x+3). Напишите уравнение этой касательной.
Угловой коэффициент данной прямой (k_1=11).
Угловой коэффициент перпендикулярной прямой (k_2=-frac=-frac) begin f'(x)=left(fracright)’-x’=frac-1=frac=\ =frac=- frac end В точке касания: begin f'(x_0)=k_2Rightarrow=-frac=-fracRightarrow (x+3)^2=121Rightarrow (x+3)^2-11^2=0Rightarrow\ Rightarrow (x+14)(x+8)=0Rightarrow left[ begin x=-14\ x=8 end right. end
Уравнение касательной при (x_0=-14) begin f(x_0)=frac+14=frac+14=-18+14=-4\ y=-frac(x+14)-4=-frac end Уравнение касательной при (x_0=8) begin f(x_0)=frac-8=frac-8=-2\ y=-frac(x-8)-2=-frac end
Ответ: точка касания (-14;-4), уравнение (y=-frac)
и точка касания (8;-2), уравнение (-frac)
Пример 4*. Найдите уравнения общих касательных к параболам (y=x^2-5x+6) и (y=x^2+x+1). Укажите точки касания.
Найдем производные функций: begin f_1′(x)=2x-5, f_2′(x)=2x+1 end Пусть a – абсцисса точки касания для первой параболы, b — для второй.
Запишем уравнения касательных (g_1(x)) и (g_2(x)) через эти переменные. begin g_1(x)=f_1′(a)(x-a)+f_1(a)=(2a-5)(x-a)+a^2-5a+6=\ =(2a-5)x-2a^2+5a+a^2-5a+6=(2a-5)x+(6-a^2)\ \ g_2(x)=f_2′(b)(x-b)+f_2(b)=(2b+1)(x-b)+b^2+b+1=\ =(2b+1)x-2b^2-b+b^2+b+1=(2b+1)x+(1-b^2) end Для общей касательной должны быть равны угловые коэффициенты и свободные члены. Получаем систему уравнений: begin begin 2a-5=2b+1\ 6-a^2=1-b^2 end Rightarrow begin 2(a-b)=6\ a^2-b^2=5 end Rightarrow begin a-b=3\ (a-b)(a+b)=5 end Rightarrow begin a-b=3\ a+b=frac53 end Rightarrow \ Rightarrow begin 2a=3+frac53\ 2b=frac53-3 end Rightarrow begin a=frac73\ b=-frac23 end end Находим угловой коэффициент и свободный член из любого из двух уравнений касательных: $$ k=2a-5=2cdotfrac73-5=-frac13, b=6-a^2=6-frac=frac59 $$ Уравнение общей касательной: $$ y=-frac x3+frac59 $$
Точки касания: begin a=frac73, f_1(a)=left(frac73right)^2-5cdotfrac73+6=frac-frac+6=frac=-frac29\ b=-frac23, f_2(b)=left(-frac23right)^2-frac23+1=frac49-frac23+1frac=frac79 end
Ответ: касательная (y=-frac x3+frac59); точки касания (left(frac73;-frac29right)) и (left(-frac23;frac79right))
Пример 5*. Докажите, что кривая (y=x^4+3x^2+2x) не пересекается с прямой (y=2x-1), и найдите расстояние между их ближайшими точками.
Решим уравнение: (x^4+3x^2+2x=2x-1) begin x^4+3x^2+1=0Rightarrow D=3^2-4=5Rightarrow x^2=frac<-3pmsqrt> end Оба корня отрицательные, а квадрат не может быть отрицательным числом.
Значит, (xinvarnothing) — решений нет, кривая и прямая не пересекаются.
Что и требовалось доказать.
Чтобы найти расстояние, необходимо построить касательную к кривой с тем же угловым коэффициентом (k=2), то и y данной прямой. Тогда искомым расстоянием будет расстояние от точки касания до прямой (y=2x-1).
Строим уравнение касательной. По условию: (f'(x)=4x^3+6x+2=2) begin 4x^3+6x=0Rightarrow 2x(2x^2+3)=0Rightarrow left[ begin x=0\ 2x^2+3=0 end right. Rightarrow left[ begin x=0\ x^2=-frac32 end right. Rightarrow left[ begin x=0\ xinvarnothing end right. Rightarrow x=0 end Точка касания (x_0=0, y_0=0^4+3cdot 0^2+2cdot 0=0).
Уравнение касательной: (y=2(x-0)+0=2x)
 | Ищем расстояние между двумя параллельными прямыми: (y=2x) и (y=2x-1). Перпендикуляр из точки (0;0) на прямую (y=2x-1) имеет угловой коэффициент (k=-frac12), его уравнение: (y=-frac12 x+b). Т.к. точка (0;0) принадлежит этому перпендикуляру, он проходит через начало координат и (b=0). |
Уравнение перпендикуляра: (y=-frac x2).
Находим точку пересечения прямой (y=2x-1) и перпендикуляра (y=-frac x2): begin 2x-1=-frac x2Rightarrow 2,5x=1Rightarrow x=0,4; y=-frac=-0,2 end Точка пересечения A(0,4;-0,2).
Находим расстояние (OA=sqrt=0,2sqrt=frac<sqrt>)
Ответ: (frac<sqrt>)
🎦 Видео
Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Как написать уравнения касательной и нормали | МатематикаСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Уравнения касательной и нормали к кривой, заданной в неявном видеСкачать

10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

№970. Напишите уравнение окружности, проходящей через точку А (1; 3), если известноСкачать

№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать

Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать

4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

Составляем уравнение прямой по точкамСкачать

Уравнение касательной в точке. Практическая часть. 2ч. 10 класс.Скачать

№967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).Скачать

Уравнение окружности (1)Скачать



 . По условию
. По условию  . Отсюда
. Отсюда  .
. 




