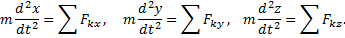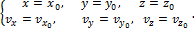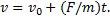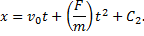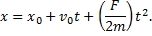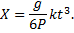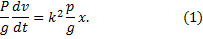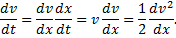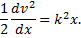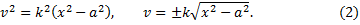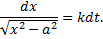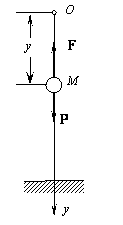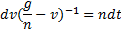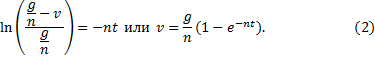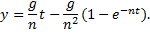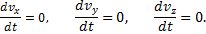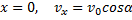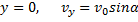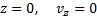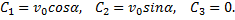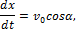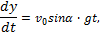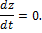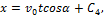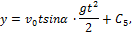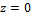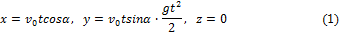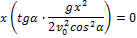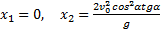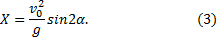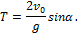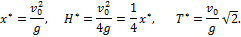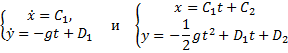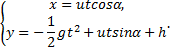Найдите уравнение движения точки вдоль оси х движущейся с постоянной скоростью v0 под углом

Точка движется с постоянной скоростью v_o под углом α к оси x. В начальный момент времени t = 0 точка имела координаты (х_o; у_o). Написать уравнения движения точки и уравнение траектории.

Решение (исправлено 25.11.2010):

Начальные координаты заданы x_o, y_o. Проекции скорости найдем из прямоугольного треугольника АВС:

v_x = −v_ocos α, знак минус указывает на то, что направление проекции вектора скорости не совпадает с направлением оси x;

v_y = v_osin α, проекция скорости положительна, так как направление вектора скорости, совпадает с направлением оси Y.

Тогда, подставляя проекции скоростей в соответствующие уравнения движения, имеем:
x = x_o − v_ot·cos α,
y = y_o + v_ot·sin α.

Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Дифференциальные уравнения движения точки

С помощью дифференциальных уравнений движения решается вторая задача динамики. Правила составления таких уравнений зависят от того, каким способом хотим определить движение точки.

1) Определение движения точки координатным способом.

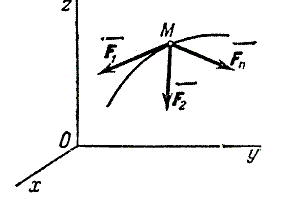
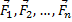
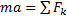
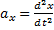
Рассмотрим свободную материальную точку, движущуюся под действием сил . Проведем неподвижные координатные оси Oxyz (рис.20). Про­ектируя обе части равенства на эти оси и учитывая, что и т.д., получим дифферен­циальные уравнения криволинейного дви­жения точки в проекциях на оси прямо­угольной декартовой системы координат:

Рис.20

Так как действующие на точку силы мо­гут зависеть от времени, от положения точки и от ее скорости, то правые части уравнений могут содержать время t, координаты точки х, у, z и проекции ее скорости 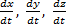. При этом в правую часть каждого из уравнений могут входить все эти переменные.

Чтобы с помощью этих уравнений решить основную задачу динамики, надо, кроме действующих сил, знать еще начальные условия, т.е. положение и скорость точки в начальный момент. В координатных осях Oxyz начальные условия задаются в виде: при t=0

Зная действующие силы, после интегрирования уравнений найдем координаты х, y, z движущейся точки, как функции времени t, т.е. найдем закон движения точки.

Пример 17. Найти закон движения материальной точки массы m, движущейся вдоль оси х под действием постоянной по модулю силы F (рис. 20.1) при начальных условиях: 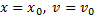при t=0.

Рис.20.1

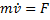
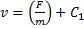
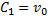
Решение. Составим дифференциальное уравнение движения точки в проекции на ось х: . Интегрируя это уравнение, находим: . Постоянная C₁ определяется из начального условия для скорости и равна . Окончательно

Далее, учитывая, что v = dx/dt, приходим к дифференциальному уравнению: 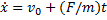, интегрируя которое получаем

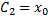
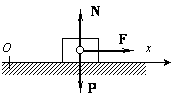
Постоянную C₂ определяем из начального условия для координаты точки. Она равна . Следовательно, закон движения точки имеет вид

Пример 18. Груз веса Р (рис.20.2) начинает двигаться из состояния покоя вдоль гладкой горизонтальной плоскости под действием силы F = kt. Найти закон движения груза.

Рис.20.2

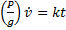
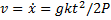
Решение. Выберем начало отсчета системы координат О в начальном положении груза и направим ось х в сторону движения (рис. 20.2). Тогда начальные условия имеют вид: x(t = 0) = 0, v(t = 0) = 0. На груз действуют силы F, P и сила реакции плоскости N. Проекции этих сил на ось х имеют значения F_x = F = kt, Р_x = 0, N_x = 0, поэтому соответствующее уравнение движения можно записать так: . Разделяя переменные в этом дифференциальном уравнении и затем интегрируя, получим: v = gkt 2 /2P + C₁. Подставляя начальные данные (v(0) = 0), находим, что C₁ = 0, и получаем закон изменения скорости .

Последнее выражение, в свою очередь, является дифференциальным уравнением, интегрируя которое найдем закон движения материальной точки: 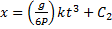. Входящую сюда постоянную определяем из второго начального условия х(0) = 0. Легко убедиться, что C₂=0. Окончательно

Пример 19. На груз, находящийся в покое на горизонтальной гладкой плоскости (см. рис. 20.2) на расстоянии a от начала координат, начинает действовать в положительном направлении оси x сила F = k 2 (P/g)x, где Р – вес груза. Найти закон движения груза.

Решение. Уравнение движения рассматриваемого груза (материальной точки) в проекции на ось х

Начальные условия уравнения (1) имеют вид: x(t = 0) = a, v(t = 0) = 0.

Входящую в уравнение (1) производную по времени от скорости представим так

Подставляя это выражение в уравнение (1) и сокращая на (P/g), получим

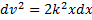
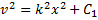
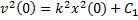
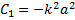
Разделяя переменные в последнем уравнении, находим, что . Интегрируя последнее, имеем: . Используя начальные условия , получаем , и, следовательно,

Поскольку сила действует на груз в положительном направлении оси х, то ясно, что в том же направлении он должен и двигаться. Поэтому в решении (2) следует выбрать знак «плюс». Заменяя дальше во втором выражении (2) v на dx/dt, получаем дифференциальное уравнение для определения закона движения груза. Откуда, разделяя переменные, имеем

Интегрируя последнее, находим: arch x/a=kt+C₂. После нахождения постоянной C₂ окончательно получаем

arch x/a=kt или .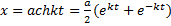

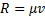
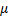
Пример 20. Шар M массы m (рис.20.3) падает без начальной скорости под действием силы тяжести. При падении шар испытывает сопротивление , где – постоянный коэффициент сопротивления. Найти закон движения шара.

Рис.20.3

Решение. Введем систему координат с началом в точке местоположения шара при t = 0, направив ось у вертикально вниз (рис. 20.3). Дифференциальное уравнение движения шара в проекции на ось у имеет тогда вид

. (1)

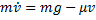
Начальные условия для шара записываются так: y(t = 0) = 0, v(t = 0) = 0.

Разделяя переменные в уравнении (1)

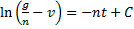
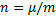
и интегрируя, находим: , где . Или после нахождения постоянной

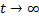
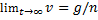
Отсюда следует, что предельная скорость, т.е. скорость при , равна .

Чтобы найти закон движения, заменим в уравнении (2) v на dy/dt. Тогда, интегрируя полученное уравнение с учетом начального условия, окончательно находим

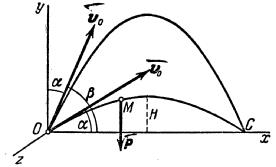
Пример 21. Изучим движение тела, брошенного с начальной скоростью v₀ под углом 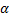к горизонту, рассматривая его как материальную точку массы т (рис.21). При этом сопротивлением воздуха пренебрежём, а поле тяжести будем считать однородным (Р=const), полагая, что дальность полёта и высота траектории малы по сравнению с радиусом Земли.

Рис.21

Поместим начало координат О в начальном положении точки. Направим ось Oy вертикально вверх; горизонтальную ось Ox расположим в плоскости, проходящей через Оy и вектор v₀, а ось Oz проведём перпендикулярно первым двум осям (рис.21). Тогда угол между вектором v₀ и осью Ox будет равен .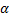

Изобразим движущуюся точку М где-нибудь на траектории. На точку действует одна только сила тяжести 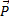, проекции которой на оси координат равны: P_x=0, P_y=-P=-mg, P_z=0.

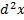
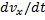
Подставляя эти величины в дифференциальные уравнения и замечая, что /dt = и т.д. мы после сокращения на m получим:

Умножая обе части этих уравнений на dt и интегрируя, находим:

Начальные условия в нашей задаче имеют вид:

Удовлетворяя начальным условиям, будем иметь:

Подставляя эти значения С₁, С₂ и С₃ в найденное выше решение и заменяя v_x, v_y, v_z на 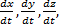придём к уравнениям:

Интегрируя эти уравнения, получим:

Подстановка начальных данных даёт С₄=С₅=С₆=0, и мы окончательно находим уравнения движения точки М в виде:

Из последнего уравнения следует, что движение происходит в плоскости Оxy.

Имея уравнение движения точки, можно методами кинематики определить все характеристики данного движения.

1. Траектория точки. Исключая из первых двух уравнений (1) время t, получим уравнение траектории точки:

Это — уравнение параболы с осью, параллельной оси Оy. Таким образом, брошенная под углом к горизонту тяжёлая точка движется в безвоздушном пространстве по параболе (Галилей).

2. Горизонтальная дальность. Определим горизонтальную дальность, т.е. измеренное вдоль оси Оx расстояние ОС=Х. Полагая в равенстве (2) y=0, найдём точки пересечения траектории с осью Ох. Из уравнения:

получаем

Первое решение дает точку О, второе точку С. Следовательно, Х=Х₂ и окончательно

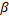
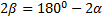
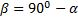
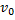
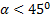
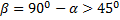
Из формулы (3) видно, что такая же горизонтальная дальность X будет получена при угле , для которого , т.е. если угол . Следовательно, при данной начальной скорости в одну и ту же точку С можно попасть двумя траекториями: на­стильной ( ) и навесной ( ).

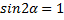
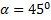
При заданной начальной скорости V₀ наибольшая горизонтальная дальность в безвоздушном пространстве получается, когда , т.е. при угле .

3. Высота траектории. Если положить в уравнении (2)

, то найдется высота траектории Н:

. (4)

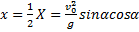
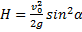
4. Время полета. Из первого уравнения системы (1) следует, что полное время полета Т определяется равенством 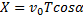. Заменяя здесь Х его значением, получим

При угле наибольшей дальности 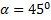все найденные вели­чины равны:

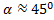
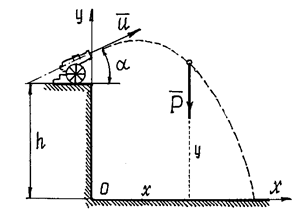
Полученные результаты практически вполне приложимы для ориен­тировочного определения характеристик полета снарядов (ракет), имеющих дальности порядка 200…600 км, так как при этих дальностях (и при ) снаряд основную часть своего пути проходит в стратосфере, где сопротивлением воздуха можно пренебречь. При меньших дальностях на результат будет сильно влиять сопротивле­ние воздуха, а при дальностях свыше 600 км силу тяжести уже нельзя считать постоянной.

Пример 22. Из пушки, установленной на высоте h, произвели выстрел под углом 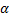к горизонту (рис. 22). Ядро вылетело из ствола орудия со скоростью u. Определим уравнения движения ядра.

Рис.22

Чтобы правильно составить дифференциальные уравнения движения, надо решать подобные задачи по определённой схеме.

а) Назначить систему координат (количество осей, их направление и начало координат). Удачно выбранные оси упрощают решение.

б) Показать точку в промежуточном положении. При этом надо проследить за тем, чтобы координаты такого положения обязательно были положительными (рис.22).

в) Показать силы, действующие на точку в этом промежуточном положении (силы инерции не показывать!).

В этом примере – это только сила 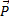, вес ядра. Сопротивление воздуха учитывать не будем.

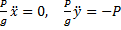
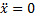
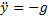
г) Составить дифференциальные уравнения по формулам: . Отсюда получим два уравнения: и .

д) Решить дифференциальные уравнения.

Полученные здесь уравнения – линейные уравнения второго порядка, в правой части – постоянные. Решение этих уравнений элементарно.

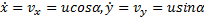
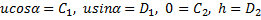
Осталось найти постоянные интегрирования. Подставляем начальные условия (при t = 0 x = 0, y = h, ) в эти четыре уравнения: .

Подставляем в уравнения значения постоянных и записываем уравнения движения точки в окончательном виде

Имея эти уравнения, как известно из раздела кинематики, можно определить и траекторию движения ядра, и скорость, и ускорение, и положение ядра в любой момент времени.

Как видно из этого примера, схема решения задач довольно проста. Сложности могут возникнуть только при решении дифференциальных уравнений, которые могут оказаться непростыми.

Видео:Механика. Кинематика. Задача на уравнение движения.Скачать

Помогите пожалуйста, Точка движется с постоянной скоростью vo под углом a к оси x?

Химия | 5 — 9 классы

Помогите пожалуйста, Точка движется с постоянной скоростью vo под углом a к оси x.

В начальный момент времени t = 0 точка имела координаты (хо ; уо).

Написать уравнения движения точки и уравнение траектории.

X = xo + v(снизуx)t по осиxи

y = yo + v(снизуy)t по осиY.

T = (xo− x) / (vo * cosa), тогда y = yo + vosin α * (xo− x) / (vo * cosa) = yo + xo * tg α − x tg α.

Видео:Уравнение движения тела дано в виде x=2−3t. ВычислиСкачать

Написать уравнения реакций брома с алюминием , литием , йодоводородом , углеродом , фосфором , если они возможны ?

Написать уравнения реакций брома с алюминием , литием , йодоводородом , углеродом , фосфором , если они возможны .

Рассмотреть их окислительно восстановительной точки зрения.

Видео:Уравнение движенияСкачать

Ca + N2 помогите пожалуйста?

Ca + N2 помогите пожалуйста.

Нужно разобрать с точки зрения ОВР.

Видео:Урок 9. Проекции вектора на координатные осиСкачать

Составить и решить ионные уравнения + рассмотреть их с точки зрения ТЭД и ОВР?

Составить и решить ионные уравнения + рассмотреть их с точки зрения ТЭД и ОВР.

Видео:Траектория и уравнения движения точки. Задача 1Скачать

Составьте уравнение реакции Hg + H2SO4(конц) — — HgSO4 + SO2 + ?

Составьте уравнение реакции Hg + H2SO4(конц) — — HgSO4 + SO2 + .

. Рассмотрите реакцию с точки зрения ОВР.

Видео:Урок 37. Движение тела, брошенного под углом к горизонту (начало)Скачать

Напишите уравнения реакций, характеризующих химические свойства алюминия?

Напишите уравнения реакций, характеризующих химические свойства алюминия.

Два уравнения взаимодействия с простыми веществами, два уравнения — со сложными веществами.

Уравнение рассмотрите с точки зрения ОВР.

Видео:Решение графических задач на равномерное движениеСкачать

Составьте молекулярное уравнение реакции, соответствующее схеме N2(0) — 2N( — 3)?

Составьте молекулярное уравнение реакции, соответствующее схеме N2(0) — 2N( — 3).

Разберите его с точки зрения ОВР.

Видео:Физика 10 класс (Урок№2 - Равномерное прямолинейное движение материальной точки.)Скачать

Разобрать уравнение с точки зрения окислетельно — восстановительной реакции : 2Li + 2N2 = 2Li3N?

Разобрать уравнение с точки зрения окислетельно — восстановительной реакции : 2Li + 2N2 = 2Li3N.

Видео:Равномерное прямолинейное движение - физика 9Скачать

Когда скорость химической реакции больше в начальных или в конечных момент?

Когда скорость химической реакции больше в начальных или в конечных момент.

Видео:Урок 12. Равномерное прямолинейное движениеСкачать

Помогите пожалуйста решить задание с точкой?

Помогите пожалуйста решить задание с точкой.

Видео:Скорость и перемещение при прямолинейном равноускоренном движении. 9 класс.Скачать

Составьте молекулярное уравнение реакции, соответствующее схеме Р 0 →Р + 5?

Составьте молекулярное уравнение реакции, соответствующее схеме Р 0 →Р + 5.

Разберите его с точки зрения ОВР.

На этой странице вы найдете ответ на вопрос Помогите пожалуйста, Точка движется с постоянной скоростью vo под углом a к оси x?. Вопрос соответствует категории Химия и уровню подготовки учащихся 5 — 9 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

MgSO4 + 2KOH — — >Mg(OH)2↓ + K2SO4 Mg⁺² + SO⁻²₄ + 2K⁺ + 2OH⁻ — — >Mg(OH)2↓ + 2K⁺ + SO⁻²₄ Mg⁺² + 2OH⁻ — — >Mg(OH)2↓ AgNO3 + HCL — — >AgCL↓ + HNO3 Ag⁺ + NO⁻₃ + H⁺ + CL⁻ — — >AgCL↓ + H⁺ + NO⁻₃ Ag⁺ + CL⁻ — — >AgCL↓ FeS + 2HCL — — >H2S↑ + FeCL2 Fe⁺² + S⁻²..

А) MgSo4 + 2KOH = Mg(OH)2↓ + K2SO4 б)AgNO3 + HCl = AgCl↓ + HNO3 в)FeS + 2HCl = FeCl2 + H2S↑ г)Ba(OH)2 + FeSO4 = Fe(OH)2↓ + BaSO4↓.

Могу лишь написать их образование и среду, может чем — то поможет : 1. BaSO4 образован сильным основанием Ва(ОН)2 и сильной кислотой H2SO4, среда нейтральная, гидролизу не подвергается. 2. MgCO3 образован слабым основанием Mg(OH)2 и слабой кислотой..

Реакция электролиза хлорида калия : 2KCl = 2K + Cl2⬆️ Масса примесей : m(прим. ) = 150г * 0, 1 = 15 г Масса чистого хлорида калия : m (KCl) = 150г — 15г = 135г Масса калия : m(K) = (40 г / моль * 2 * 135г) : (75, 5 г / моль * 2) = 68, 79г.

Мед — ? 25×100 = 2500 2500÷6. 25 = 400 руд.

У них у всех не металлическое а все остальное есть в табл. Менделеева.

Ответ : Li, K, C, N, P, S, Cl.

CH₄ + Cl₂ → CH₃Cl + HCl 2CH₃Cl + 2Na → CH₃ — CH₃ + 2NaCl CH₃ — CH₃ + Br₂ → CH₃ — CH₂Br + HBr 2CH₃ — CH₂Br + 2Na → CH₃ — CH₂ — CH₂ — CH₃ + 2NaBr.

Схема реакции : CxHy — — — > xCO2 + y / 2 H2O n (CO2) = 132 / 44 = 3 моль CxHy — 1 моль CO2 — 3 моль x = 3 1 дм3 — 1, 961 г. N (CxHy) = 1дм3 / 22, 4 дм3 / моль = 0, 0446 моль M (CxHy) = 1, 961 г / 0, 0446 моль = 44 г / моль С3Hy = 12 * 3 + y = 44 г ..

А) кристаллизация ; б) конденсация ; в) испарение ; г) конденсация.

📸 Видео

Кинематика точки Задание К1Скачать

Урок 15. Решение задач на графики движенияСкачать

Кинематика точки. Три способа задания движения. Скорость, ускорениеСкачать

Движение тела, брошенного под углом к горизонтуСкачать

Задача из ЕГЭ по физике │Анализ графика #1Скачать

Вращательное движение. 10 класс.Скачать

УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать