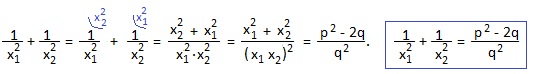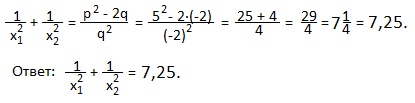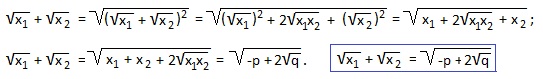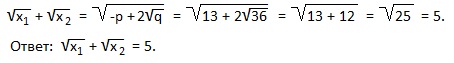Найдите сумму обратных величин корней уравнения x2 px q

Часто требуется найти сумму квадратов (x₁ 2 +x₂ 2 ) или сумму кубов (x₁ 3 +x₂ 3 ) корней квадратного уравнения, реже — сумму обратных значений квадратов корней или сумму арифметических квадратных корней из корней квадратного уравнения:

Помочь в этом может теорема Виета:

Сумма корней приведенного квадратного уравнения x 2 +px+q=0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:

Выразим через p и q:

1) сумму квадратов корней уравнения x 2 +px+q=0;

2) сумму кубов корней уравнения x 2 +px+q=0.

Решение.

1) Выражение x₁ 2 +x₂ 2 получится, если взвести в квадрат обе части равенства x₁+x₂=-p;

(x₁+x₂) 2 =(-p) 2 ; раскрываем скобки: x₁ 2 +2x₁x₂+ x₂ 2 =p 2 ; выражаем искомую сумму: x₁ 2 +x₂ 2 =p 2 -2x₁x₂=p 2 -2q. Мы получили полезное равенство: x₁ 2 +x₂ 2 =p 2 -2q.

2) Выражение x₁ 3 +x₂ 3 представим по формуле суммы кубов в виде:

Еще одно полезное равенство: x₁ 3 +x₂ 3 =-p·(p 2 -3q).

Примеры.

3) x 2 -3x-4=0. Не решая уравнение, вычислите значение выражения x₁ 2 +x₂ 2 .

Решение.

По теореме Виета сумма корней этого приведенного квадратного уравнения

x₁+x₂=-p=3, а произведение x₁∙x₂=q=-4. Применим полученное нами (в примере 1) равенство:

x₁ 2 +x₂ 2 =p 2 -2q. У нас -p=x₁+x₂=3 → p 2 =3 2 =9; q=x₁x₂=-4. Тогда x₁ 2 +x₂ 2 =9-2·(-4)=9+8=17.

4) x 2 -2x-4=0. Вычислить: x₁ 3 +x₂ 3 .

Решение.

По теореме Виета сумма корней этого приведенного квадратного уравнения x₁+x₂=-p=2, а произведение x₁∙x₂=q=-4. Применим полученное нами (в примере 2) равенство: x₁ 3 +x₂ 3 =-p·(p 2 -3q)=2·(2 2 -3·(-4))=2·(4+12)=2·16=32.

Ответ: x₁ 3 +x₂ 3 =32.

Вопрос: а если нам дано не приведенное квадратное уравнение? Ответ: его всегда можно «привести», разделив почленно на первый коэффициент.

5) 2x 2 -5x-7=0. Не решая, вычислить: x₁ 2 +x₂ 2 .

Решение. Нам дано полное квадратное уравнение. Разделим обе части равенства на 2 (первый коэффициент) и получим приведенное квадратное уравнение: x 2 -2,5x-3,5=0.

По теореме Виета сумма корней равна 2,5; произведение корней равно -3,5.

Решаем так же, как пример 3), используя равенство: x₁ 2 +x₂ 2 =p 2 -2q.

x₁ 2 +x₂ 2 =p 2 -2q=2,5 2 -2∙(-3,5)=6,25+7=13,25.

Ответ: x₁ 2 +x₂ 2 =13,25.

6) x 2 -5x-2=0. Найти:

Преобразуем это равенство и, заменив по теореме Виета сумму корней через -p, а произведение корней через q, получим еще одну полезную формулу. При выводе формулы использовали равенство 1): x₁ 2 +x₂ 2 =p 2 -2q.

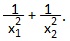
В нашем примере x₁+x₂=-p=5; x₁∙x₂=q=-2. Подставляем эти значения в полученную формулу:

7) x 2 -13x+36=0. Найти:

Преобразуем эту сумму и получим формулу, по которой можно будет находить сумму арифметических квадратных корней из корней квадратного уравнения.

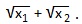
У нас x₁+x₂=-p=13; x₁∙x₂=q=36. Подставляем эти значения в выведенную формулу:

Совет: всегда проверяйте возможность нахождения корней квадратного уравнения по подходящему способу, ведь 4 рассмотренные полезные формулы позволяют быстро выполнить задание, прежде всего, в тех случаях, когда дискриминант — «неудобное» число. Во всех простых случаях находите корни и оперируйте ими. Например, в последнем примере подберем корни по теореме Виета: сумма корней должна быть равна 13, а произведение корней 36. Что это за числа? Конечно, 4 и 9. А теперь считайте сумму квадратных корней из этих чисел: 2+3=5. Вот так то!

Видео:Найти значение суммы и произведения корней квадратного уравненияСкачать

Найдите сумму обратных величин корней уравнения x2 px q

OBRAZOVALKA.COM — образовательный портал
Наш сайт это площадка для образовательных консультаций, вопросов и ответов для школьников и студентов .

На вопросы могут отвечать также любые пользователи, в том числе и педагоги.

Консультацию по вопросам и домашним заданиям может получить любой школьник или студент.

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Найдите сумму обратных величин корней уравнения x2 px q

Известно, что квадратное уравнение x 2 + px + q = 0 имеет два различных натуральных корня.

а) Найдите все возможные значения p, если q = 26.

б) Найдите все возможные значения q, если q + p = 72.

в) Найдите все возможные значения корней уравнения, если q 2 − p 2 = 2812.

а) По теореме Виета произведение этих корней равно 26, поэтому сами они равны 13 и 2 или 26 и 1. При этом откуда p = −15 или p = −27.

б) Получаем уравнение откуда значит, и или наоборот. В любом случае

Числа и отличаются друг от друга на чётное число, поэтому они одной чётности, поэтому каждое из них делится на 2 и не делится на 4. Кроме того, поэтому остаются такие варианты:

а) и

б) и

Рассмотрим первый случай: Натуральными решениями второго уравнения являются пары чисел (4; 2) или (2; 4), которые не являются решениями первого уравнения. Поэтому этот случай не приводит к решениям.

Рассмотрим второй случай: Всевозможные натуральные решения второго уравнения это (40; 2), (14; 4), (4; 14), (2; 40). Первому уравнению удовлетворяют только пары (14; 4) и (4; 14).

Ответ: а) −27 или −15; б) 148; в) 4 и 14.

Частично дублирует задание 526680 из основной волны ЕГЭ 2019 года.

Аналоги к заданию № 526680: 526701 562497 Все

Видео:Не решая квадратное уравнение, найдите сумму кубов его корнейСкачать

Теорема Виета

Теорема Виета:

Сумма корней приведённого квадратного уравнения

равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену

Если приведённое квадратное уравнение имеет вид

то его корни равны:

,

где D = p 2 — 4q. Чтобы доказать теорему, сначала найдём сумму корней:

,

а теперь найдём их произведение:

Равенства, показывающие зависимость между корнями и коэффициентами квадратного уравнения:

называются формулами Виета.

Примечание: если дискриминант равен нулю (D = 0), то подразумевается, что уравнение имеет не один корень, а два равных корня.

Видео:#67. Сумма квадратов корней в уравнении с параметром!Скачать

Обратная теорема

Теорема:

Если сумма двух чисел равна -p, а их произведение равно q, то эти числа являются корнями приведённого квадратного уравнения:

Это доказывает, что число x₁ является корнем уравнения x 2 + px + q = 0. Точно так же можно доказать, что и число x₂ является корнем для этого уравнения.

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Решение примеров

Зависимость между корнями и коэффициентами квадратного уравнения позволяет в некоторых случаях находить корни уравнения устно, не используя формулу корней.

Пример 1. Найти корни уравнения:

Решение: Так как

очевидно, что корни равны 1 и 2:

Подставив числа 1 и 2 в уравнение, убедимся, что корни найдены правильно:

1 2 — 3 · 1 + 2 = 0

2 2 — 3 · 2 + 2 = 0.

Пример 2. Найти корни уравнения:

Методом подбора находим, что корни равны -3 и -5:

С помощью теоремы, обратной теореме Виета, можно составлять квадратное уравнение по его корням.

Пример 1. Составить квадратное уравнение по его корням:

Решение: Так как x₁ = -3, x₂ = 6 корни уравнения x 2 + px + q = 0, то по теореме, обратной теореме Виета, составим уравнения:

Следовательно, искомое уравнение:

Пример 2. Записать приведённое квадратное уравнение, имеющее корни:

📸 Видео

ТЕОРЕМА ВИЕТА ЗА 2 МИНУТЫСкачать

Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Алгебра 8 класс (Урок№19 - Уравнение х² = а.)Скачать

Свойства квадратного корня. Уравнение х2=а, 8 классСкачать

Математика Один из корней уравнения 3x^2 +5x +2m =0 равен -1. Найдите второй корень.Скачать

САМЫЙ ПРОСТОЙ СПОСОБ ПОНЯТЬ ТЕОРЕМУ ВИЕТА #shorts #математика #егэ #огэ #теорема #теоремавиетаСкачать

Найдите корни уравнения: cosπ(x−7)/3=1/2 В ответ запишите наибольший отрицательный корень.Скачать

Как решать квадратные уравнения. 8 класс. Вебинар | МатематикаСкачать

Решение биквадратных уравнений. 8 класс.Скачать

Найдите корень уравнения 2^(4-2x) = 64Скачать

Алгебра 8 класс. Сумма корнейСкачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

При каких значениях а сумма квадратов корней уравнения x² + ax + a - 2 = 0 минимальна?Скачать

Теорема Виета. 8 класс.Скачать

ЕГЭ по математике. Профильный уровень. Задание 5. Найдите корень уравненияСкачать