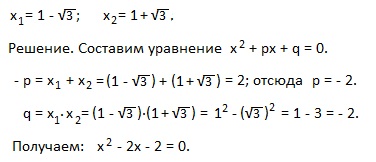I. Теорема Виета для приведенного квадратного уравнения.
Сумма корней приведенного квадратного уравнения x 2 +px+q=0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:
Найти корни приведенного квадратного уравнения, используя теорему Виета.
Пример 1) x 2 -x-30=0. Это приведенное квадратное уравнение ( x 2 +px+q=0), второй коэффициент p=-1, а свободный член q=-30. Сначала убедимся, что данное уравнение имеет корни, и что корни (если они есть) будут выражаться целыми числами. Для этого достаточно, чтобы дискриминант был полным квадратом целого числа.
Находим дискриминант D=b 2 — 4ac=(-1) 2 -4∙1∙(-30)=1+120=121=11 2 .
Теперь по теореме Виета сумма корней должна быть равна второму коэффициенту, взятому с противоположным знаком, т.е. (-p), а произведение равно свободному члену, т.е. (q). Тогда:
x1+x2=1; x1∙x2=-30. Нам надо подобрать такие два числа, чтобы их произведение было равно -30, а сумма – единице. Это числа -5 и 6. Ответ: -5; 6.
Пример 2) x 2 +6x+8=0. Имеем приведенное квадратное уравнение со вторым коэффициентом р=6 и свободным членом q=8. Убедимся, что есть целочисленные корни. Найдем дискриминант D1, так как второй коэффициент – четное число. D1=3 2 -1∙8=9-8=1=1 2 . Дискриминант D1 является полным квадратом числа 1, значит, корни данного уравнения являются целыми числами. Подберем корни по теореме Виета: сумма корней равна –р=-6, а произведение корней равно q=8. Это числа -4 и -2.
На самом деле: -4-2=-6=-р; -4∙(-2)=8=q. Ответ: -4; -2.
Пример 3) x 2 +2x-4=0. В этом приведенном квадратном уравнении второй коэффициент р=2, а свободный член q=-4. Найдем дискриминант D1, так как второй коэффициент – четное число. D1=1 2 -1∙(-4)=1+4=5. Дискриминант не является полным квадратом числа, поэтому, делаем вывод: корни данного уравнения не являются целыми числами и найти их по теореме Виета нельзя. Значит, решим данное уравнение, как обычно, по формулам (в данном случае по формулам для частного случая с четным вторым коэффициентом). Получаем:
Пример 4). Составьте квадратное уравнение по его корням, если x1=-7, x2=4.
Решение. Искомое уравнение запишется в виде: x 2 +px+q=0, причем, на основании теоремы Виета –p=x1+x2=-7+4=-3 → p=3; q=x1∙x2=-7∙4=-28. Тогда уравнение примет вид: x 2 +3x-28=0.
Пример 5). Составьте квадратное уравнение по его корням, если:
II. Теорема Виета для полного квадратного уравнения ax 2 +bx+c=0.
Сумма корней равна минус b, деленному на а, произведение корней равно с, деленному на а:
Пример 6). Найти сумму корней квадратного уравнения 2x 2 -7x-11=0.
Решение.
Убеждаемся, что данное уравнение будет иметь корни. Для этого достаточно составить выражение для дискриминанта, и, не вычисляя его, просто убедиться, что дискриминант больше нуля. D=7 2 -4∙2∙(-11)>0. А теперь воспользуемся теоремой Виета для полных квадратных уравнений.
Пример 7). Найдите произведение корней квадратного уравнения 3x 2 +8x-21=0.
Решение.
Найдем дискриминант D1, так как второй коэффициент (8) является четным числом. D1=4 2 -3∙(-21)=16+63=79>0. Квадратное уравнение имеет 2 корня, по теореме Виета произведение корней x1∙x2=c:a=-21:3=-7.
Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Найдите сумму квадратного уравнения x2 px q 0
Известно, что квадратное уравнение x 2 + px + q = 0 имеет два различных натуральных корня.
а) Найдите все возможные значения p, если q = 26.
б) Найдите все возможные значения q, если q + p = 72.
в) Найдите все возможные значения корней уравнения, если q 2 − p 2 = 2812.
а) По теореме Виета произведение этих корней равно 26, поэтому сами они равны 13 и 2 или 26 и 1. При этом откуда p = −15 или p = −27.
б) Получаем уравнение откуда
значит,
и
или наоборот. В любом случае
Числа и
отличаются друг от друга на чётное число, поэтому они одной чётности, поэтому каждое из них делится на 2 и не делится на 4. Кроме того,
поэтому остаются такие варианты:
а) и
б) и
Рассмотрим первый случай:
Натуральными решениями второго уравнения являются пары чисел (4; 2) или (2; 4), которые не являются решениями первого уравнения. Поэтому этот случай не приводит к решениям.
Рассмотрим второй случай:
Всевозможные натуральные решения второго уравнения это (40; 2), (14; 4), (4; 14), (2; 40). Первому уравнению удовлетворяют только пары (14; 4) и (4; 14).
Ответ: а) −27 или −15; б) 148; в) 4 и 14.
Частично дублирует задание 526680 из основной волны ЕГЭ 2019 года.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Верно получены результаты пунктов а, б, в. | 4 |
| Верно получены результаты пунктов (а или б) и в. | 3 |
| Верно получены результаты пунктов (а и б) или в | 2 |
| Верно получены результаты пунктов а или б. | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 4 |
Аналоги к заданию № 526680: 526701 562497 Все
Видео:Найти значение суммы и произведения корней квадратного уравненияСкачать

Теорема Виета
Теорема Виета:
Сумма корней приведённого квадратного уравнения
равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену
Если приведённое квадратное уравнение имеет вид
то его корни равны:

где D = p 2 — 4q. Чтобы доказать теорему, сначала найдём сумму корней:

а теперь найдём их произведение:
Равенства, показывающие зависимость между корнями и коэффициентами квадратного уравнения:
называются формулами Виета.
Примечание: если дискриминант равен нулю (D = 0), то подразумевается, что уравнение имеет не один корень, а два равных корня.
Видео:Уравнение x^2+px+q=0 имеет корни -6; 4. Найдите q. | ОГЭ 2017 | ЗАДАНИЕ 4 | ШКОЛА ПИФАГОРАСкачать

Обратная теорема
Теорема:
Если сумма двух чисел равна -p, а их произведение равно q, то эти числа являются корнями приведённого квадратного уравнения:
Это доказывает, что число x1 является корнем уравнения x 2 + px + q = 0. Точно так же можно доказать, что и число x2 является корнем для этого уравнения.
Видео:Формула корней квадратного уравнения. Алгебра, 8 классСкачать

Решение примеров
Зависимость между корнями и коэффициентами квадратного уравнения позволяет в некоторых случаях находить корни уравнения устно, не используя формулу корней.
Пример 1. Найти корни уравнения:
Решение: Так как
очевидно, что корни равны 1 и 2:
Подставив числа 1 и 2 в уравнение, убедимся, что корни найдены правильно:
1 2 — 3 · 1 + 2 = 0
2 2 — 3 · 2 + 2 = 0.
Пример 2. Найти корни уравнения:
Методом подбора находим, что корни равны -3 и -5:
С помощью теоремы, обратной теореме Виета, можно составлять квадратное уравнение по его корням.
Пример 1. Составить квадратное уравнение по его корням:
Решение: Так как x1 = -3, x2 = 6 корни уравнения x 2 + px + q = 0, то по теореме, обратной теореме Виета, составим уравнения:
Следовательно, искомое уравнение:
Пример 2. Записать приведённое квадратное уравнение, имеющее корни:
🔍 Видео
Решение биквадратных уравнений. 8 класс.Скачать

Алгебра 8 класс (Урок№19 - Уравнение х² = а.)Скачать

Теорема Виета. 8 класс.Скачать

Теорема Виета. Алгебра, 8 классСкачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

СУММА КОЭФФИЦИЕНТОВ: Как решать Квадратные Уравнения по МАТЕМАТИКЕ 8 классСкачать

ТЕОРЕМА ВИЕТА ЗА 2 МИНУТЫСкачать

САМЫЙ ПРОСТОЙ СПОСОБ ПОНЯТЬ ТЕОРЕМУ ВИЕТА #shorts #математика #егэ #огэ #теорема #теоремавиетаСкачать

Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

ТЕОРЕМА ВИЕТА // Как решать Квадратные Уравнения по АЛГЕБРЕ 8 классСкачать

№1 Квадратное уравнение х^2+x-6=0 Дискриминант, теорема ВиетаСкачать

Неполные квадратные уравнения. Алгебра, 8 классСкачать

Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать

Теорема Виета - Тестовые задания I частьСкачать

Квадрат суммы и квадрат разности двух выражений. 7 класс.Скачать