Найдите радиус окружности заданной уравнением x2 y2 2x 10y 23 0

Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Нахождение центра и радиуса окружности по общему уравнению окружности

Этот калькулятор проверяет, является ли введенное уравнение общим уравнением окружности, и вычисляет координаты центра и радиуса окружности, если это возможно. Описание способа решения подобных задач находится под калькулятором

Нахождение центра и радиуса окружности по общему уравнению окружности

Уравнение НЕ является общим уравнением окружности

Приведение общего уравнения окружности к стандартному виду

Калькулятор выше можно применять для решения задач на уравнение окружности. Чаще всего вы имеете дело с уравнением окружности, выраженном в так называемом стандартном виде

Из этого уравнения достаточно легко найти центр окружности — это будет точка с координатами (a,b), и радиус окружности — это будет квадратный корень из правой части уравнения.

Однако, если возвести в квадрат выражения в скобках и перенести правую часть налево, то уравнение станет выглядеть примерно так:

Это — уравнение окружности в общем виде. Здесь радиус и центр окружности уже не выделены явно, и в задачах обычно просят их найти именно по общему виду уравнения окружности.

Способ решения такого рода задач следующий:

Перегруппируем слагаемые уравнения

Как видим, выражение в конце это уравнение окружности в стандартном виде, из которого уже легко получить и координаты центра окружности и ее радиус. Если же справа получилось отрицательное число — значит заданное вначале уравнение не является уравнением окружности (бывают задачи и на такую проверку). Калькулятор тоже проверяет это условие.

Для решения обратной задачи — нахождения общего уравнения окружности по координатам центра и радиусу — можно использовать калькулятор Уравнение окружности по заданному центру и радиусу в различных формах

Видео:Найти центр и радиус окружностиСкачать

Радиус окружности, заданной уравнением x ^ 2 + y ^ 2 — 2y = 0, равен?

Геометрия | 10 — 11 классы

Радиус окружности, заданной уравнением x ^ 2 + y ^ 2 — 2y = 0, равен.

так как все это равно 0.

Видео:№578. Найдите координаты центра и радиус сферы, заданной уравнением: а) х2+y2+z2 = 49; б) (x — 3)2Скачать

Найдите длину окружности, если радиус окружности равен 5?

Найдите длину окружности, если радиус окружности равен 5.

Видео:Геометрия Украденная задача Найти радиусСкачать

Помогите пожалуйста?

Определите радиус окружности , заданной уравнением.

Видео:Найти радиус. Задача на вниманиеСкачать

Окружность задана уравнением (х — 3)² + (у + 2)² = 25 найдите радиус окружности и координаты ее центра?

Окружность задана уравнением (х — 3)² + (у + 2)² = 25 найдите радиус окружности и координаты ее центра.

Видео:Найдите радиус окружностиСкачать

Найдите длины дуг, на которые разбивают окружность два радиуса?

Найдите длины дуг, на которые разбивают окружность два радиуса.

Угол между радиусами равен 120, радиус окружности равен 6 дм.

Видео:Составить уравнение окружности. Геометрия. Задачи по рисункам.Скачать

Найдите координаты центра и радиус окружности заданной уравнением?

Найдите координаты центра и радиус окружности заданной уравнением.

Видео:Радиус описанной окружностиСкачать

Диаметр окружности равен 88 км?

Диаметр окружности равен 88 км.

Чему равен радиус окружности?

Видео:Задача 6 №27910 ЕГЭ по математике. Урок 130Скачать

Окружность задана уравнением x в квадрате + y в квадрате = 16 ?

Окружность задана уравнением x в квадрате + y в квадрате = 16 .

Найдите радиус окружности и начертите ее в системе координат xOy.

Видео:Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

Окружность задана уравнением (x + 3) ^ 2 + y ^ 2 = 36?

Окружность задана уравнением (x + 3) ^ 2 + y ^ 2 = 36.

Определить радиус и координаты центра окружности.

Видео:Уравнение окружности (1)Скачать

Диаметр окружности равен 4а?

Диаметр окружности равен 4а.

Укажите радиус окружности.

Видео:Задача 6 №27859 ЕГЭ по математике. Урок 104Скачать

Чему равен радиус окружности описанной около равностороннего треугольника, если радиус, вписанной в него окружности, равен 2 см?

Чему равен радиус окружности описанной около равностороннего треугольника, если радиус, вписанной в него окружности, равен 2 см?

Если вам необходимо получить ответ на вопрос Радиус окружности, заданной уравнением x ^ 2 + y ^ 2 — 2y = 0, равен?, относящийся к уровню подготовки учащихся 10 — 11 классов, вы открыли нужную страницу. В категории Геометрия вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.

Углы : ABD ; CBE ; ABE ; EBD ; DBC Надеюсь, я ничего не пропустила.

3x + 5x = 180. 5•22, 5 = 112, 5 8x = 180 X = 22, 5.

Во втором случае : Угол OTS = 65, угол S = 90, тогда третий угол равен 180 — (90 + 65) = 25 Угол SOT = POT по условию значит угол О равен 50. Угол OPS равен 180 — (90 + 50) = 40.

Углы 75 и 105 — односторонние, в сумме дают 180гр, следовательно АС║ЕД угол ЕДВ и угол СВД — накрест лежащие, т. Е. равны. СВД = 52гр треугольник ВСД — равнобедренный, значит углы при основании равны. Сумма углов треугольника равна 180, следовател..

В равнобедренном треугольнике АВС ВД — высота и биссектриса, значит∠АВС = 60°. ∠ВАС = ∠ВСА = (180 — ∠АВС) / 2 = 60°. В треугольнике АВС все углы равны, значит он равносторонний. Высота равностороннего треугольника h = a√3 / 2, a = 2h / √3 = 2h√3 /..

Отрезок CD является расстоянием от точки C до AD.

Один кут дорівнює 110 градусів, тому що вертикальні кути рівні, тобто 220 / 2 = 110 а сума суміжних кутів дорівнює 180 градусів, тобто невідомий кут 180 — 110 = 70 градусів.

Нехай AB і CD перетинаються. Тоді за аксіомою С3 через них можна провести площину. Цій площині належать прямі AB і CD, а отже, і точки A, B, C, D, що суперечить умові задачі.

Я уже отвечал 90°, т. К. между хордами из одной точки окружности проведённые к диаметру угог равен 90°.

А как тебе решать, если ничего не дано в условии.

Видео:Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать

Уравнение окружности.

Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.

В формулировке окружности упоминается расстояние между точкой окружности и центром.

Формула расстояния между двумя точками М₁(х₁; у₁) и М₂(х₂; у₂) имеет вид:

,

Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х₀; у₀) и радиусом r.

Отметим произвольную точку М(х; у) на этой окружности.

.

Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.

Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х₀ ) 2 +(у – у₀ ) 2 = r 2 .

Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х₀; у₀) и радиусом r имеет вид:

В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):

Видео:Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

Нахождение центра и радиуса окружности по общему уравнению окружности

Этот калькулятор проверяет, является ли введенное уравнение общим уравнением окружности, и вычисляет координаты центра и радиуса окружности, если это возможно. Описание способа решения подобных задач находится под калькулятором

Нахождение центра и радиуса окружности по общему уравнению окружности

Уравнение НЕ является общим уравнением окружности

Приведение общего уравнения окружности к стандартному виду

Калькулятор выше можно применять для решения задач на уравнение окружности. Чаще всего вы имеете дело с уравнением окружности, выраженном в так называемом стандартном виде

Из этого уравнения достаточно легко найти центр окружности — это будет точка с координатами (a,b), и радиус окружности — это будет квадратный корень из правой части уравнения.

Однако, если возвести в квадрат выражения в скобках и перенести правую часть налево, то уравнение станет выглядеть примерно так:

Это — уравнение окружности в общем виде. Здесь радиус и центр окружности уже не выделены явно, и в задачах обычно просят их найти именно по общему виду уравнения окружности.

Способ решения такого рода задач следующий:

Перегруппируем слагаемые уравнения

Как видим, выражение в конце это уравнение окружности в стандартном виде, из которого уже легко получить и координаты центра окружности и ее радиус. Если же справа получилось отрицательное число — значит заданное вначале уравнение не является уравнением окружности (бывают задачи и на такую проверку). Калькулятор тоже проверяет это условие.

Для решения обратной задачи — нахождения общего уравнения окружности по координатам центра и радиусу — можно использовать калькулятор Уравнение окружности по заданному центру и радиусу в различных формах

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

как найти центр и радиус окружности, когда. x^2 + y^2 + z^2 = 10y x +2y + 2z = 19

Центр сферы в точке (0,5,0). Напишем параметрические
уравнения прямой, проходящей через этот центр и
перпендикулярной к плоскости. Нормаль к плоскости:
вектор N(1,2,2). Уравнения прямой:

x=t, y=5+2t, z=2t, здесь t — параметр.

Пересечение прямой и плоскости — искомый центр (x0,y0,z0)
окружности: t+10+4t+4t=19, отсюда t=1.

Итак, x0=1, y0=7, z0=2.

Для нахождения радиуса найдите какую-нибудь точку на
окружности и подсчитайте её расстояние до центра.

📽️ Видео

Задача 6 №27923 ЕГЭ по математике. Урок 140Скачать

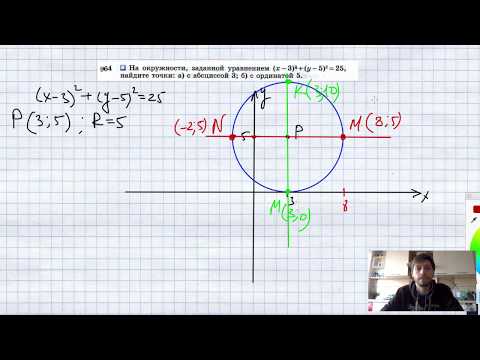
№964. На окружности, заданной уравнением (x-3)2 + + (y-5)2 = 25, найдите точки: а) с абсциссой 3;Скачать

Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать