Найдите площадь поверхности сферы заданной уравнением x2 y2 z2 4x 2y 6z 4

Видео:№578. Найдите координаты центра и радиус сферы, заданной уравнением: а) х2+y2+z2 = 49; б) (x — 3)2Скачать

x^2+y^2+z^2+2z+4y+6z+a=0 определите при каких значениях а

Возможно, вы имели ввиду: «Определите, в каких значениях а задает сферу».
Если да, то вот ответ:
Х²+y²+z²+2х+4y+6z+a=0
Уравнение сферы: (x–a)²+(y–b)²+(z–c)²=R²
Сгруппируем переменные: (х²+2х)+(у²+4у)+(z²+6z)+a=0
По каждой переменной выделим полный квадрат:
(х²+2∙1x+1)+(у²+2∙2у+4)+(z²+2∙3z+9) – 14+a=0
(x+1)²+(у+2)²+(z+3)²–14+a=0
(x+1)²+(у+2)²+(z+3)²=14–a
Тогда 14–а=R², следовательно 14–a>0
a

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Площадь сферы Урок 26 По данной теме урок 4 Классная работа 23.07.2015. — презентация

Презентация была опубликована 6 лет назад пользователемТимур Казаченко

Похожие презентации

Видео:№579. Докажите, что каждое из следующих уравнений является уравнением сферы. Найдите координатыСкачать

Презентация на тему: » Площадь сферы Урок 26 По данной теме урок 4 Классная работа 23.07.2015.» — Транскрипт:

1 Площадь сферы Урок 26 По данной теме урок 4 Классная работа

2 О Дано: MN — двугранный угол, MN =120, сфера (О; R) касается граней двугранного угла в точках А и В, d(MN, O) = a. Найти: R, AB. 591 А В С M N А C B O Решение: ОА, ОВ по свойству касательной плоскости. ОА = ОВ = R. ОС MN по тереме о трех перпендикулярах. ОС = а. ОВС = ОАС (ОС – общая, ОВ=ОА=R), значит, ОС – биссектриса АСВ, значит, ОСА = 60. ОСА: ОАВ — равносторонний ( ВОА = 30, СОА = 30, значит, ВОА = 30 и ОА = ОВ = R.) Проверка домашнего задания

3 578 Проверка домашнего задания 576

4 п. 58 – (б, в, г), 595, 598, 597, 600

5 Повторение 1. Сфера задана уравнением: x2 + y2 + z2 + 2y – 4z = 4. Найдите координаты центра и радиус сферы. Решение: x2 + y2 + z2 + 2y – 4z = 4. Выделим квадрат двучлена: x2 + y2 + 2y z2 – 4z = 4; x2 + (y + 1) (z – 2) = 4; x2 + (y + 1)2 + (z – 2)2 = = = = 9; С(0; -1; 2); R = 3. Ответ: С(0; -1; 2); R = Точки А и В принадлежат шару. Принадлежат ли шару любая точка отрезка АВ? Ответ: Да.

6 Повторение 3. Могут ли все вершины прямоугольного треугольника с катетами 4 см илежать на сфере радиуса ? 4. Могут ли две сферы с общим центром и с неравными радиусами иметь общую касательную плоскость? Ответ: Нет.

7 Сфера называется вписанной в многогранник, в частности, в пирамиду, если она касается всех граней этого многогранника (пирамиды). Многогранник называется описанным, если сфера касается всех его граней. Площадью сферы называют предел последовательности площадей поверхностей, описанных около сферы многогранников при стремлении к нулю наибольшего размера каждой грани.

Видео:Геометрия 11 класс: Сфера и шар. Уравнение сферы. Площадь сферыСкачать

Вычисление площади поверхности

Вычисление площади поверхности

1. Услуги проектирования
2. Двойной интеграл
3. Вычисление площади поверхности

Видео:Найти центр и радиус окружностиСкачать

Вычисление площади поверхности

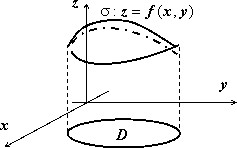
Пусть в пространстве задана кусочно-гладкая поверхность $sigma $, однозначно проектирующаяся в область $mathbf < textit > $ на плоскости $mathbf < textit > $. Пусть эта поверхность задаётся уравнением $sigma :;z=f(x,y),;(x,y)in D$. Тогда площадь этой поверхности выражается формулой

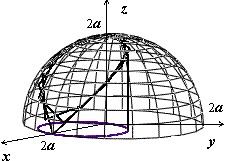
Мы докажем эту формулу позже, когда будем изучать поверхностные интегралы. Сейчас рассмотрим пример: найти площадь лепестков, вырезаемых цилиндром $mathbf < textit > ^ +mathbf < textit > ^ $ = 2$mathbf < textit > $ из сферы $mathbf < textit > ^ +mathbf < textit > ^ +mathbf < textit > ^ $ = 4$mathbf < textit > ^ $ .

Решение:

Область $mathbf < textit > $ — сдвинутый на $mathbf < textit > $ единиц по оси $mathbf < textit > $ круг, поэтому вычисляем в полярных координатах, учитывая симметрию поверхности относительно плоскостей $mathbf < textit > $ и $mathbf < textit > $:

Вычислить площадь cферы радиуса (a.)

Решение:

Рассмотрим верхнюю полусферу. Ее уравнение имеет вид $ < + + = > ;; < text ;;z = sqrt < — — > . > $

Очевидно, область интегрирования (R) представляет собой круг с таким же радиусом (a,) расположенный в центре координат. Площадь полусферы вычисляется по формуле $ < S_ < largefrac normalsize > > = iintlimits_R < sqrt < 1 + < < left( < frac < > < > >right) > ^2 > + < < left( < frac < > < > >right) > ^2 > > dxdy > .$

Площадь поверхности полной сферы, соответственно, равна $S = 2 < S_ < largefrac normalsize > > = 4pi .$

Далее:

Критерий полноты . Лемма о нелинейной функции

Вычисление криволинейного интеграла второго рода. Примеры.

Вычисление двойного интеграла

СДНФ. Теорема о представлении в виде СДНФ. Построение СДНФ по таблице

Полином Жегалкина. Пример.

Вычисление площади поверхности

Несобственные интегралы по неограниченной области

Теорема об алгоритме распознавания полноты

Введение

Класс Te . Теорема о замкнутости Te

Формулы. Равенство функций и эквивалентность формул. Основные эквивалентности

Формула Грина

Примеры применения цилиндрических и сферических координат

Односторонние и двусторонние поверхности. Ориентация поверхности

Нахождение потенциала

Огравление $Rightarrow $

🎥 Видео

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

11 класс, 20 урок, Уравнение сферыСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

11 класс, 19 урок, Сфера и шарСкачать

Применение определенного интеграла при решении геометр. и физических задач. Практ. часть. 11 класс.Скачать

Площадь треугольника. Как найти площадь треугольника?Скачать

Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Геометрия 11 класс (Урок№8 - Сфера и шар.)Скачать

Задание 3 ЕГЭ по математике. Урок 11Скачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Стереометрия, номер 10.1Скачать

Диагностическая работа в формате ОГЭ. Задача-11Скачать

Математика без Ху!ни. Смешанное произведение векторовСкачать