В этом разделе мы продолжим разбирать тему вычисления площадей плоских фигур. Рекомендуем тем, кто изучает темы не по порядку, сначала обратиться к статье «Геометрический смысл определенного интеграла» и разобрать способы вычисления площади криволинейной трапеции. Нам понадобится вычислять площади фигур, которые ограничены ограничены линиями y = f ( x ) , x = g ( y ) в прямоугольной системе координат. А также раздел «Свойства площади фигур», где была разобрана квадрируемость плоских фигур.
- Краткий обзор статьи
- Полярная система координат и криволинейный сектор
- Площадь криволинейного сектора — вывод формулы
- Примеры вычисления площади криволинейного сектора
- Площадь фигуры, которую ограничивает лемниската Бернулли
- Площадь фигуры, границей которой является кардиоида
- Площадь фигуры, которую ограничивает улитка Паскаля
- Площадь фигур, границей которых является спираль Архимеда или логарифмическая спираль
- Нахождение площади фигуры, которую можно представить как разность двух криволинейных секторов
- Найдите площадь фигуры ограниченной линией заданной уравнением в полярных координатах онлайн
- Контакты
- Вычислить площадь фигуры, ограниченной линиями
- Вычислить площадь фигуры, ограниченной кривыми онлайн
- 🎬 Видео
Видео:Площадь фигуры через двойной интеграл в полярных координатахСкачать

Краткий обзор статьи
- Начнем с определения понятия криволинейного сектора, получим формулу для вычисления его площади. Для этого мы используем понятие определенного интеграла Дарбу.
- Подробно разберем решения задач с использованием таких кривых как кардиоида, архимедова спираль и лемниската Бернулли.
- В отдельную подтему мы выделили нахождение площади фигуры, которая представлена как разность двух криволинейных секторов.
Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Полярная система координат и криволинейный сектор
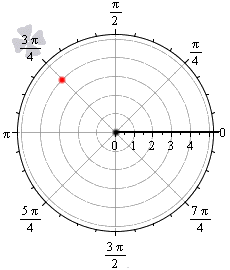
Точка, расположенная в полярной системе координат, имеет полярный угол φ 0 и полярный радиус r 0 ≥ 0 . Полярный угол φ 0 отсчитывается от полярной оси по часовой стрелке, а r 0 — это расстояние от заданной точки до начала координат.
На рисунке мы отметили начало координат (полюс) жирной черной точкой, полярная ось имеет вид луча черного цвета, а красная точка определяется углом φ 0 = 3 π 4 и расстоянием до полюса r 0 = 4 .
Мы можем рассматривать полярную систему координат одновременно с прямоугольной декартовой. Для этого необходимо совместить начала координат обеих систем, а ось абсцисс и полярной осью.
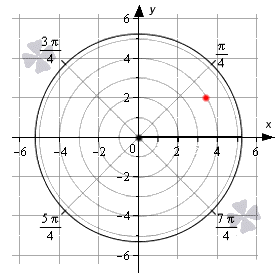
Задать связь полярных и декартовых координат можно соотношениями r = x 2 + y 2 φ = a r c t g y x , x ≠ 0 и обратно x = r · cos φ y = r · sin φ .
Координаты красной точки на чертеже 2 3 ; 2 . Положение этой точки задается углом φ 0 = a r c t g 2 2 3 = π 6 и расстоянием r 0 = 2 3 2 + 2 2 = 4 .
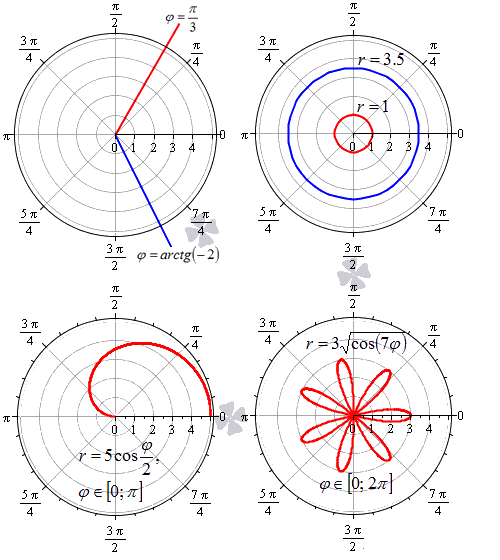
В полярной системе координат равенство φ = α задает луч, который выходит из точки начала координат и составляет угол α с полярной осью. При этом, угол α может быть задан как в радианах, так и в градусах. Полярную ось мы можем задать уравнением вида φ = 0 . Равенство r = C > 0 задает окружность с центром в начале координат, где — это радиус.
Функция r = p ( φ ) , φ ∈ α ; β определяет некоторую линию в полярных координатах.
Следует учитывать тот факт, что с позиции геометрии функция r = p ( φ ) , φ ∈ α ; β во всех случаях будет неотрицательной. Связано это с тем, что она задает расстояние от начала координат до точки для заданного значения угла φ = φ 0 ∈ α ; β . Однако мы будем встречать и отрицательные значения r = p ( φ ) функции, что зависит от отношения к данному вопросу конкретных исследователей и преподавателей.
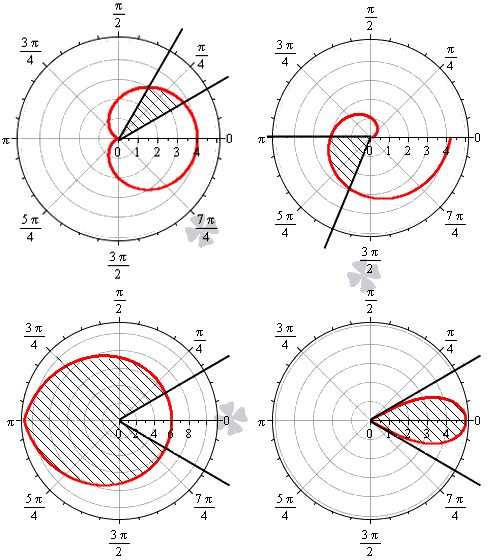
На рисунке мы изобразили несколько примеров линий в полярной системе координат.
Дадим определение криволинейному сектору.
Криволинейный сектор представляет собой фигуру, которая ограничена лучами φ = α , φ = β и некоторой линией r = p ( φ ) ≥ 0 , непрерывной на участке α ; β .
На рисунке мы привели несколько примеров криволинейных секторов.
На последнем рисунке мы рассмотрели случай, когда фигура располагается между лучами φ = — π 6 , φ = π 6 , которые не являются ее границами.
Видео:Площадь фигуры, заданной в полярной системе координатСкачать

Площадь криволинейного сектора — вывод формулы
Для вычисления площади криволинейного сектора мы можем вывести формулу. Для этого мы можем использовать формулу площади кругового сектора радиуса R с внутренним углом γ из школьного курса геометрии: S к р у г о в о г о с е к т о р а = γ · R 2 2 . Задаем внутренний угол γ в радианах.
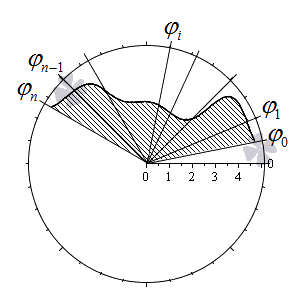
Разобьем криволинейный сектор на n частей такими лучами
φ = φ 1 , φ = φ 2 , . . . , φ = φ n — 1 , что α = φ 0 φ 1 φ 2 . . . φ n — 1 β и λ = m a x i = 1 , 2 , . . . , n φ i — φ i — 1 → 0 при n → + ∞ .
Учитывая свойства площади фигуры, мы можем представить площадь исходного криволинейного сектора S ( G ) как сумму площадей секторов S ( G i ) на каждом из участков разбиения:
S ( G ) = ∑ i = 1 n S ( G i )
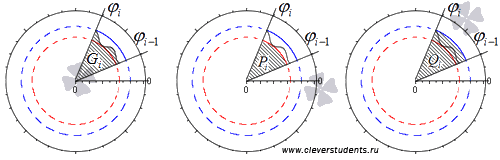
Обозначим наибольшее и наименьшее значения функции r = p ( φ ) на i -ом отрезке φ i — 1 ; φ i , i = 1 , 2 , . . . , n как R m i n i и R m a x i . На каждом из отрезков построим по два круговых сектора P i и Q i с максимальным и минимальным радиусами R m i n i и R m a x i соответственно.
Фигуры, которые являются объединением круговых секторов Q i , i = 1 , 2 , . . . , n ; P i , i = 1 , 2 , . . . , n , обозначим как P и Q соответственно.
Их площади будут равны S ( P ) = ∑ i = 1 n S ( P i ) = ∑ i = 1 n 1 2 ( R m i n i ) 2 · φ i — φ i — 1 и S ( Q ) = ∑ i = 1 n S ( Q i ) = ∑ i = 1 n 1 2 ( R m a x i ) 2 · φ i — φ i — 1 , причем S ( P ) ≤ S ( G ) ≤ S ( Q ) .
Так как функция r = p φ непрерывна на отрезке α ; β , то функция 1 2 p 2 φ будет непрерывна на этом отрезке. Если рассматривать S ( P ) и S ( Q ) для этой функции как нижнюю и верхнюю суммы Дарбу, то мы можем прийти к равенству:
lim λ → 0 S ( P ) = lim λ → 0 S ( Q ) = S ( G ) ⇒ S ( G ) = lim λ → 0 ∑ i = 1 n 1 2 ( R m i n i ) 2 · φ i — φ i — 1 = = lim λ → 0 ∑ i = 1 n 1 2 ( R m a x i ) · φ i — φ i — 1 = 1 2 ∫ β α p 2 φ d φ
Формула для определения площади криволинейного сектора имеет вид:
S ( G ) = 1 2 ∫ β α p 2 φ d φ
Видео:Площади 12Скачать

Примеры вычисления площади криволинейного сектора
Рассмотрим алгоритмы вычисления площади криволинейного сектора с полярной системе координат на конкретных примерах.
Необходимо вычислить площадь плоской фигуры в полярных координатах, которая ограничена линией r = 2 sin 2 φ и лучами φ = π 6 , φ = π 3 .
Решение
Для начала, изобразим описанную в условии задачи фигуру в полярной системе координат. Функция r = 2 sin ( 2 φ ) положительна и непрерывна на отрезке φ ∈ π 6 , π 3 .
Полученная фигура является криволинейным сектором, что позволяет нам применить формулу для нахождения площади этого сектора.
S ( G ) = 1 2 ∫ π 6 π 3 ( 2 sin ( 2 φ ) 2 d φ = ∫ π 6 π 3 2 ( sin ( 2 φ ) 2 d φ = ∫ π 6 π 3 2 · 1 — cos 4 φ 2 d φ = ∫ π 6 π 3 ( 1 — cos ( 4 φ ) ) d φ = φ — 1 4 sin ( 4 φ ) π 6 π 3 = = π 3 — 1 4 sin 4 π 3 — π 6 — 1 4 sin 4 π 6 = π 6 + 3 4
Ответ: S ( G ) = π 6 + 3 4
Задача упрощается в тех случаях, когда лучи φ = φ 1 , φ = φ 2 , ограничивающие фигуру, заданы. Тогда нам не нужно задумываться о пределах интегрирования при проведении вычисления площади.
Чаще встречаются задачи, где фигуру ограничивает лишь кривая r = p ( φ ) . В этих случаях применить формулу S ( G ) = 1 2 ∫ α β p 2 ( φ ) d φ сразу не получится. Для начала придется решить неравенство p ( φ ) ≥ 0 для нахождения пределов интегрирования. Так мы можем поступить в тех случаях, когда функция r = p φ неотрицательная. В противном случае нам придется ориентироваться только на область определения и период функции.
Необходимо вычислить площадь фигуры, которая ограничена кривой в полярных координатах r = — 3 · cos 3 φ .
Решение
Функция определена для всех действительных значений аргумента. Решим неравенство — 3 · cos 3 φ ≥ 0 :
— 3 · cos 3 φ ≥ 0 ⇔ cos 3 φ ≤ 0 ⇔ cos φ ≤ 0 ⇔ ⇔ π 2 + 2 πk ≤ φ ≤ 3 π 2 + 2 πk , k ∈ Z
Построим функцию в полярных координатах на отрезке φ ∈ π 2 ; 3 π 2 (при k = 0 ). Для других значений k в силу периодичности косинуса мы будем получать ту же самую кривую.
Применим формулу для вычисления площади фигуры в полярных координатах. В качестве нижнего и верхнего предела можно брать π 2 + 2 πk и 3 π 2 + 2 πk соответственно для любого целого значения k .
S ( G ) = 1 2 ∫ π 2 3 π 2 ( — 3 · cos 3 φ ) d φ = 9 2 ∫ π 2 3 π 2 cos 6 φ d φ
Для того, чтобы получить ответ, нам необходимо вычислить полученный определенный интеграл. Для этого мы можем использовать формулу Ньютона-Лейбница. Первообразную для формулы Ньютона-Лейбница мы можем с помощью рекуррентной формулы вида K n ( x ) = sin x · cos n — 1 ( x ) n + n — 1 n K n — 2 ( x ) , где K n ( x ) = ∫ cos n ( x ) d x .
∫ cos 6 φ d φ = sin φ · cos 5 φ 6 + 5 6 ∫ cos 4 φ d φ = = sin φ · cos 5 φ 6 + 5 6 sin φ · cos 3 φ 4 + 3 4 cos 2 φ d φ = = sin φ · cos 5 φ 6 + 5 sin φ · cos 3 φ 24 + 15 24 sin φ · cos φ 2 + 1 2 ∫ cos 0 φ d φ = = ∫ π 2 3 π 2 cos 6 φ d φ = sin φ · cos 5 φ 6 + 5 sin φ · cos 3 φ 24 + 15 sin φ · cos φ 48 + 15 φ 48 π 2 3 π 2 = = 15 48 · 3 π 2 — 15 48 · π 2 = 5 π 16
Таким образом, искомая площадь фигуры, ограниченной линией в полярной системе координат, равна S ( G ) = 9 2 ∫ π 2 3 π 2 cos 6 φ d φ = 9 2 · 5 π 16 = 45 π 32 .
Ответ: S ( G ) = 45 π 32
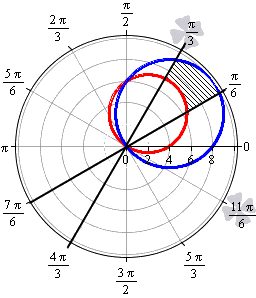
В тех случаях, когда в полярной системе координат задается множество кривых, которые по форме напоминают листья клевера или цветка, площадь фигур, ограниченных этими кривыми, часто одинаковы. В этих случаях можно вычислить площадь одного «лепестка» и умножить ее на количество криволинейных фигур.
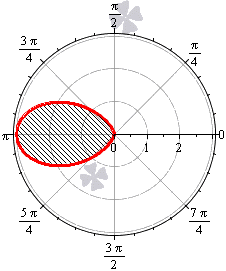
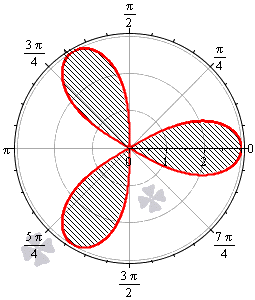
Необходимо вычислить площадь плоской фигуры в полярной системе координат, которая ограничена линией r = 3 · cos ( 3 φ ) .
Решение
Найдем область определения, исходя из того, что эта функция неотрицательна для любого φ из области определения.
cos ( 3 φ ) ≥ 0 ⇔ — π 2 + 2 πk ≤ 3 φ ≤ π 2 + 2 πk , k ∈ Z — π 6 + 2 π 3 k ≤ φ ≤ π 6 + 2 π 3 k , k ∈ Z
Таким образом, период функции r = 3 · cos 3 φ равен 2 π 3 . Это значит, что фигура состоит из трех областей одинаковой площади.
Построим фигуру на графике.
Вычислим площадь одного участка, расположенного на интервале φ ∈ π 2 ; 5 π 6 (при k = 1 ):
1 2 ∫ π 2 5 π 6 9 cos ( 3 φ ) d φ = 1 2 · 3 sin ( 3 φ ) π 2 5 π 6 = 3 2 sin 3 · 5 π 6 — sin 3 · π 2 = 3 2 ( 1 — ( — 1 ) = 3
Ответ: Площадь всей фигуры будет равна площади найденного участка, умноженной на 3.
Аналогичным образом можно найти площади фигур, имеющих сходное строение. Примером может служить лемниската Бернулли.
Видео:Построение кривой в полярной системе координатСкачать

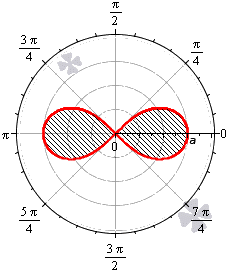
Площадь фигуры, которую ограничивает лемниската Бернулли
Лемниската Бернулли задается уравнением r = α · cos 2 φ где a – положительное число, влияющее на размер линии (но не на конфигурацию, схожую с символом бесконечности). Лемниската Бернулли строится при — π 4 + π · k ≤ φ ≤ π 4 + π · k , k ∈ Z .
Лемниската служит границей фигуры, которую можно представить как два равных по площади участка.
Для вычисления площади используем нужную формулу:
S ( G ) = 2 · 1 2 ∫ — π 4 π 4 a 2 cos ( 2 φ ) 2 φ = a 2 2 ( sin ( 2 φ ) ) — π 4 π 4 = = a 2 2 sin 2 · π 4 — sin 2 · — π 4 = a 2
Получается, что площадь фигуры, которую ограничивает лемниската Бернулли, равна квадрату коэффициента a .
Видео:Глаза гипножабы и площадь фигур в полярной системе координатСкачать

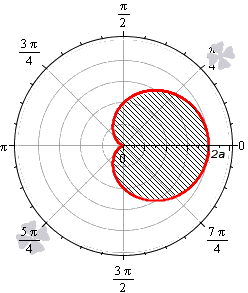
Площадь фигуры, границей которой является кардиоида
В полярной системе координат кардиоида задается уравнением вида r = 2 a ( 1 + cos φ ) . В этом уравнении a – некоторое положительное число. Задающая кардиоиду функция является периодической с периодом 2 π . Она определена для всех действительных значений угла. Это значит, что для вычисления площади нижним пределом интегрирования мы будем считать любое число, а верхним, то, которое на 2 π больше нижнего.
Вычислим площадь фигуры, ограниченной кардиоидой r = 2 a ( 1 + cos φ ) , для φ ∈ 0 ; 2 π :
S ( G ) = 1 2 ∫ 0 2 π ( 2 a ( 1 + cos φ ) ) 2 d φ = 2 a 2 ∫ 0 2 π ( 1 + 2 cos φ + cos 2 φ ) d φ = = 2 a 2 ∫ 0 2 π 1 + 2 cos φ + 1 + cos 2 φ 2 d φ = = 2 a 2 ∫ 0 2 π 3 2 + 2 cos φ + cos ( 2 φ ) 2 d φ = = 2 a 2 3 2 φ + 2 sin φ + 1 4 sin 2 φ 0 2 π = 6 π · a 2
Видео:Найти площадь фигуры, ограниченной линиями. Пример 1.Скачать
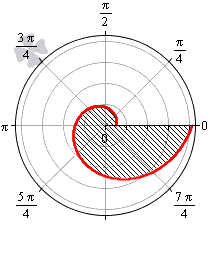
Площадь фигуры, которую ограничивает улитка Паскаля
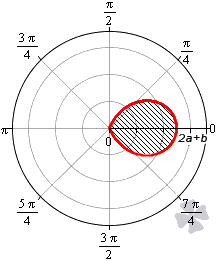
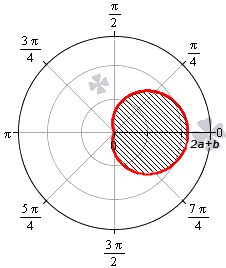
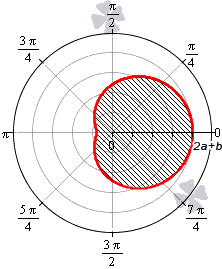
В полярной системе координат улитка Паскаля может быть задана уравнением r = b + 2 a · cos φ . В этом уравнении a – это некоторое положительное число, b – любое действительное число. Кардиоиду можно рассматривать как частный случай улитки Паскаля. Получить кардиоиду можно при b = 2 a .
Улитка Паскаля в зависимости от значений параметров a и b может принимать различный вид. В данном разделе мы рассмотрим случаи, когда функцию r неотрицательная.
При b — 2 a функция r = b + 2 a · cos φ будет отрицательной для любого значения угла φ .
При b = — 2 a улитка Паскаля имеет вид точки, которая совпадает с полюсом.
При — 2 a b 0 функция r = b + 2 a · cos φ неотрицательна для φ ∈ — a r c cos — b 2 a + 2 πk ; arccos — b 2 a + 2 πk , k ∈ Z .
При 0 b 2 a функция r = b + 2 a · cos φ неотрицательна для φ ∈ — a r c cos — b 2 a + 2 πk ; arccos — b 2 a + 2 πk , k ∈ Z . Она ограничивает фигуру, которая по конфигурации напоминает кардиоиду.
При b > 2 a функция r = b + 2 a · cos φ является неотрицательной для любого значения угла. Графическая иллюстрация этого случая приведена ниже
Для того, чтобы правильно определить пределы интегрирования, необходимо учитывать соотношение параметров a и b .
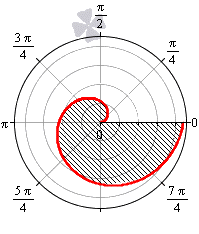
Необходимы вычислить площадь фигуры, которая ограничена линиями, заданными уравнениями r = — 3 + 6 cos φ и r = 5 + 4 cos φ в полярной системе координат.
Решение
Формула r = — 3 + 6 cos φ соответствует фигуре, известной как улитка Паскаля..
Функция r = — 3 + 6 cos φ определена для всех значений угла φ . Нам необходимо выяснить, при каких φ функция будет неотрицательной:
— 3 + 6 cos φ ≥ 0 ⇔ cos φ ≥ 1 2 ⇔ — π 3 + 2 π k ≤ φ ≤ π 3 + 2 πk , k ∈ Z
Проведем вычисление площади фигуры, которая ограничена данной улиткой Паскаля:
S ( G ) = 1 2 ∫ — π 3 π 3 ( — 3 + 6 cos φ ) 2 d φ = 9 2 ∫ — π 3 π 3 ( 1 — 4 cos φ + 4 cos 2 φ ) d φ = = 9 2 ∫ — π 3 π 3 1 — 4 cos φ + 4 · 1 + cos 2 φ 2 d φ = = 9 2 ∫ — π 3 π 3 ( 3 — 4 cos φ + 2 cos ( 2 φ ) ) d φ = 9 2 · 3 φ — 4 sin φ + sin ( 2 φ — π 3 π 3 = = 9 2 · 3 · π 3 — 4 sin π 3 + sin 2 π 3 — 3 · — π 3 — 4 sin — π 3 + sin — 2 π 3 = = 9 2 · 2 π — 3 3
Улитка Паскаля, определяемая формулой r = 5 + 4 cos φ , соответствует пятому пункту. Функция r = 5 + 4 cos φ определена и положительна для всех действительных значений φ . Поэтому, площадь фигуры в этом случае равна:
S ( G ) = 1 2 ∫ 0 2 π ( 5 + 4 cos φ ) 2 d φ = 1 2 ∫ 0 2 π ( 25 + 40 cos φ + 16 cos 2 φ ) d φ = = 1 2 ∫ 0 2 π 25 + 40 cos φ + 16 · 1 + cos ( 2 φ ) 2 d φ = = 1 2 ∫ 0 2 π ( 33 + 40 cos φ + 8 cos ( 2 φ ) ) d φ = 1 2 · 33 φ + 40 sin φ + 4 sin ( 2 φ 0 2 π = = 1 2 · 33 · 2 π + 40 sin ( 2 π + 4 sin ( 4 π ) — 33 · 0 + 40 sin 0 + 4 sin 0 = 33 π
Ответ: S ( G ) = 33 π
Видео:Математика без Ху!ни. Определенные интегралы, часть 3. Площадь фигуры.Скачать

Площадь фигур, границей которых является спираль Архимеда или логарифмическая спираль
Сразу обратимся к примеру.
Необходимо вычислить площадь фигур в полярной системе координат, первая из которых ограничена первым витком спирали Архимеда r = α φ , α > 0 , а вторая первым витком логарифмической спирали r = α φ , α > 1 .
Решение
Если в задаче сказано, что фигура ограничена первым витком спирали Архимеда, то угол φ изменяется от нуля до двух пи.
Исходя из этого, найдем площадь фигуры по формуле:
S ( G ) = 1 2 ∫ 0 2 π ( α φ ) 2 d ϕ = α 2 2 ∫ 0 2 π φ 2 d φ = α 2 2 · φ 3 3 0 2 π = 4 α 3 π 3 3
Аналогично вычисляется площадь фигуры, ограниченной первым витком логарифмической спирали:
S ( G ) = 1 2 ∫ 0 2 π ( α ϕ ) 2 d ϕ = 1 2 ∫ 0 2 π a 2 φ d φ = 1 4 ln a · a 2 φ 0 2 π = = 1 4 ln a · a 4 π — 1
Видео:Геометрический смысл определенного интеграла (2)Скачать

Нахождение площади фигуры, которую можно представить как разность двух криволинейных секторов
Пусть фигура в полярной системе координат ограничена лучами φ = α , φ = β и непрерывными и неотрицательными на интервале φ ∈ α ; β функциями r = p 1 ( φ ) и r = p 2 ( φ ) , причем p 1 ( φ ) ≤ p 2 ( φ ) для любого угла φ = φ 0 ∈ α ; β .
Находим площадь фигуры по формуле S ( G ) = 1 2 ∫ α β p 2 2 ( φ ) — p 1 2 ( φ ) d φ .
Действительно, в силу свойства аддитивности площади, фигуру G можно представить как разность двух криволинейных секторов G 2 и G 1 .
Тогда площадь фигуры G равна разности площадей этих криволинейных секторов:
S ( G ) = S ( G 2 ) — S ( G 1 ) = 1 2 ∫ α β p 2 2 ( φ ) d φ — 1 2 ∫ α β p 1 2 ( φ ) d φ = = 1 2 ∫ α β p 2 2 ( φ ) — p 1 2 ( φ ) d φ
Последний переход возможен в силу третьего свойства определенного интеграла.
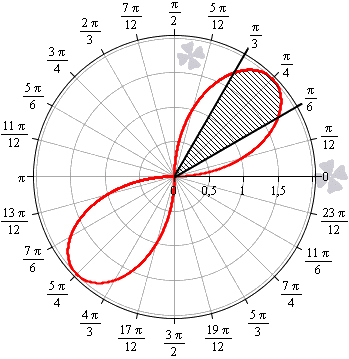
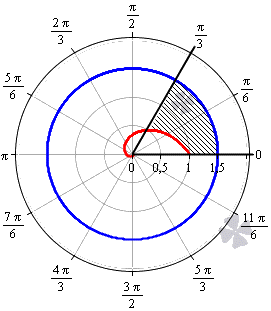
Необходимо вычислить площадь фигуры, которая ограничена линиями φ = 0 , φ = π 3 , r = 3 2 , r = 1 2 φ в полярной системе координат.
Решение
Построим заданную фигуру на графике.
Очевидно, что r = 3 2 больше r = 1 2 φ для любого φ ∈ 0 ; π 3 . Применяем полученную формулу для вычисления площади фигуры:
S ( G ) = 1 2 ∫ 0 π 3 3 2 2 — 1 2 φ 2 d φ = 1 2 ∫ 0 π 3 9 4 — 2 — 2 φ d φ = = 1 2 · 9 4 φ + 1 2 · 2 — 2 φ ln 2 0 π 3 = 1 2 · 9 4 φ + 1 ln 2 · 1 2 2 φ + 1 0 π 3 = = 1 2 · 9 4 · π 3 + 1 ln 2 · 1 2 2 · π 3 + 1 — 9 4 · 0 + 1 ln 2 · 1 2 2 · 0 + 1 = = 1 2 · 3 π 4 + 2 — 2 π 3 — 1 2 · ln 2
Ответ: S ( G ) = 1 2 · 3 π 4 + 2 — 2 π 3 — 1 2 · ln 2
А теперь рассмотрим пример, когда фигура ограничена линиями, заданными в прямоугольной системе координат. Площадь такой фигуры намного проще вычислять, используя полярные координаты.
Необходимо вычислить площадь фигуры, которая ограничена прямыми линиями y = 1 3 x , x = 3 x , окружностями ( x — 2 ) 2 + ( y — 3 ) 2 = 13 , ( x — 4 ) 2 + ( y — 3 ) 2 = 25 .
Решение
В прямоугольной системе координат вычислить площадь полученной фигуры можно, но дело это долгое и хлопотное. Намного проще перейти к полярной системе координат, воспользовавшись формулами перехода.
x = r · cos φ y = r · sin φ ⇒ y = 1 3 x ⇔ r · sin φ = r · cos φ 3 ⇔ t g φ = 1 3 ⇔ φ = π 6 + πk y = 3 x ⇔ r · sinφ = 3 · r · cosφ ⇔ tgφ = 3 ⇔ φ = π 3 + πk ( x — 2 ) 2 + ( y — 3 ) 2 = 13 ⇔ x 2 + y 2 = 4 x + 6 y ⇔ r = 4 cosφ + 6 sinφ ( x — 4 ) 2 + ( y — 3 ) 2 = 25 ⇔ x 2 + y 2 = 8 x + 6 y ⇔ r = 8 cosφ + 6 sinφ
Функция r = 8 cos φ + 6 sin φ больше r = 4 cos φ + 6 sin φ для любого φ ∈ π 6 ; π 3 . Вычисляем площадь фигуры в полярных координатах:
S ( G ) = 1 2 ∫ π 6 π 3 8 cos φ + 6 sin φ 2 — 4 cos φ + 6 sin φ 2 d φ = = 1 2 ∫ π 6 π 3 ( 48 cos 2 φ + 48 cos φ · sin φ ) d φ = = 24 ∫ π 6 π 3 cos 2 φ d φ + 24 ∫ π 6 π 3 cos φ · sin φ d φ = = 12 ∫ π 6 π 3 ( 1 + cos 2 φ ) d φ + 24 ∫ π 6 π 3 sin φ d ( sin φ ) = = 12 · φ + 1 2 sin ( 2 φ ) π 6 π 3 + 12 · sin 2 φ π 6 π 3 = = 12 · π 3 + 1 2 sin 2 π 3 — π 6 + 1 2 sin 2 π 6 + 12 · sin 2 π 3 — sin 2 π 6 = = 12 · π 6 + 12 · 3 2 2 — 1 2 2 = 2 π + 6
Видео:Найти площадь фигуры, ограниченной линиямиСкачать

Найдите площадь фигуры ограниченной линией заданной уравнением в полярных координатах онлайн
Запрошуємо усіх хто любить цікаві задачі та головоломки відвідати групу! Зараз діє акція — підтримай студента! Знижки на роботи + безкоштовні консультації.
Контакты
 |
| Основные функции |
: x^a
: Sqrt[x]
: x^(1/n)
: a^x
: Log[a, x]
: Log[x]
: cos[x] или Cos[x]
: sin[x] или Sin[x]
: tan[x] или Tan[x]
: cot[x] или Cot[x]
: sec[x] или Sec[x]
: csc[x] или Csc[x]
: ArcCos[x]
: ArcSin[x]
: ArcTan[x]
: ArcCot[x]
: ArcSec[x]
: ArcCsc[x]
: cosh[x] или Cosh[x]
: sinh[x] или Sinh[x]
: tanh[x] или Tanh[x]
: coth[x] или Coth[x]
: sech[x] или Sech[x]
: csch[x] или Csch[е]
: ArcCosh[x]
: ArcSinh[x]
: ArcTanh[x]
: ArcCoth[x]
: ArcSech[x]
: ArcCsch[x]
- [19.67] =19: integral part of (19.67) — выделяет целую часть числа (integerPart)
Предложения и пожелания пишите на [email protected]
Поделитесь этим калькулятором на форуме или в сети!
Видео:Двойной интеграл в полярных координатахСкачать

Вычислить площадь фигуры, ограниченной кривыми онлайн
Вычисление площадей плоских фигур является одним из приложений определенного интеграла.
Для того, чтобы получить площадь фигуры изображенной на рисунке, необходимо вычислить определенный интеграл вида:
Функции и как правило, известны из условия задачи, а вот абсциссы их точек пересечения и придется дополнительно найти. Для этого необходимо решить уравнение:
Описанным выше способом, можно также найти площадь криволинейной трапеции в случае, если графики функций и не пересекаются, но точки и заданы по условию задачи:
В этом случае криволинейная трапеция (фигура площадь которой мы вычисляем) образована графиками функций , и прямыми , .
Онлайн калькулятор, построенный на основе системы Wolfram Alpha, автоматически вычислит площадь фигуры, образованной пересечением двух графиков функций.
🎬 Видео
Найти площадь фигуры, ограниченной линиями. Пример 5.Скачать

Площадь фигуры, ограниченной линиямиСкачать

Вычисление площади фигуры, ограниченной заданными линиямиСкачать

Криволинейная трапеция и ее площадь. 11 класс.Скачать

Полярная система координатСкачать

Найти площадь фигуры, ограниченной линиями. Пример 4.Скачать

Полярная система координатСкачать

Вычислите площадь фигуры, ограниченной линиямиСкачать



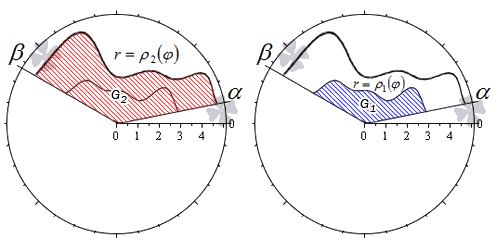


 : x^a
: x^a : Sqrt[x]
: Sqrt[x] : x^(1/n)
: x^(1/n) : a^x
: a^x : Log[a, x]
: Log[a, x] : Log[x]
: Log[x] : cos[x] или Cos[x]
: cos[x] или Cos[x] : sin[x] или Sin[x]
: sin[x] или Sin[x] : tan[x] или Tan[x]
: tan[x] или Tan[x] : cot[x] или Cot[x]
: cot[x] или Cot[x] : sec[x] или Sec[x]
: sec[x] или Sec[x] : csc[x] или Csc[x]
: csc[x] или Csc[x] : ArcCos[x]
: ArcCos[x] : ArcSin[x]
: ArcSin[x] : ArcTan[x]
: ArcTan[x] : ArcCot[x]
: ArcCot[x] : ArcSec[x]
: ArcSec[x] : ArcCsc[x]
: ArcCsc[x] : cosh[x] или Cosh[x]
: cosh[x] или Cosh[x] : sinh[x] или Sinh[x]
: sinh[x] или Sinh[x] : tanh[x] или Tanh[x]
: tanh[x] или Tanh[x] : coth[x] или Coth[x]
: coth[x] или Coth[x] : sech[x] или Sech[x]
: sech[x] или Sech[x] : csch[x] или Csch[е]
: csch[x] или Csch[е] : ArcCosh[x]
: ArcCosh[x] : ArcSinh[x]
: ArcSinh[x] : ArcTanh[x]
: ArcTanh[x] : ArcCoth[x]
: ArcCoth[x] : ArcSech[x]
: ArcSech[x] : ArcCsch[x]
: ArcCsch[x]