Парабола — это функция, заданная уравнением:
Её график имеет следующий вид:
Причем, в зависимости от знака коэффициента , ветви параболы направлены вверх (если ) или вниз (если ).
В школьном курсе алгебры возникает задача нахождения координат вершины параболы. Их можно найти по формулам:
Вершина параболы, отмечена оранжевой точкой на приведённом выше графике.
Наш онлайн калькулятор позволяет найти координаты вершины параболы с описанием подробного хода решения на русском языке. Для работы калькулятора, необходимо ввести уравнение параболы и указать её переменную. Уравнение параболы можно вводить в различных форматах, а коэффициентами могут быть не только числа или дроби, но и параметры. Нажмите на кнопку «Примеры», расположенную на панели калькулятора, чтобы посмотреть различные форматы ввода.
Видео:КАК НАЙТИ ВЕРШИНУ ПАРАБОЛЫСкачать

Парабола, график, вершина, нули.
теория по математике 📈 функции
Функция вида y=ax 2 +bx+c, где а, b, с – некоторые числа, причем, а ≠ 0 число, х – переменная, называется квадратичной функцией.
Графиком квадратичной функции является парабола, она имеет вершину и две ветви, которые могут быть направлены либо вверх, либо вниз (рис.1). Красной точкой обозначена вершина параболы, из которой выходят ветви. Её координаты по графику – (3; –4). Направление ветвей зависит от значения коэффициента «а», то есть, если «а» – положительное число, то ветви направлены вверх; если число «а» – отрицательное, то ветви направлены вверх. На данном рисунке ветви направлены вверх, значит коэффициент «а» у формулы, которая задает эту функцию – положительное число. Коэффициент «с» показывает ординату (у) точки пересечения ветви параболы с осью у. Так, на рисунке №1 парабола пересекает ось у в точке (5;0), значит коэффициент с=5.
Чтобы найти координаты вершины параболы (х0; у0), надо воспользоваться формулой:
для нахождения у0 можно просто подставить значение х0 в формулу данной функции y0=ax 2 +bx+c вместо х.
Рассмотрим это на примере конкретно заданной функции.
Пример №1
Найти вершину параболы, заданной формулой у=2х 2 – 8х + 5.
Найдем, чему равны коэффициенты: а=2; b= – 8
Подставим их в формулу и вычислим значение х0:
х0= − b 2 a . . = 8 2 ∙ 2 . . = 8 4 . . = 2
Теперь в заданную по условию формулу вместо х подставим найденное значение у0=2 ∙ 2 2 – 8 ∙ 2 + 5=8 – 16 + 5= –3
Итак, мы нашли координаты вершины параболы: (2; –3).
Значения х, при которых функция принимает значения, равные нулю, называются нулями функции. Другими словами, Значения абсцисс (х) точек пересечения ветвей параболы с осью х, называются нулями функции. На рисунке №1 точки координаты точек пересечения ветвей параболы с осью х следующие: (1;0) и (5;0). Значит, нули функции – это значения х, равные 1 и 5.
Рассмотрим, как найти нули функции не по рисунку, а по заданной формуле.
Пример №2
Найти нули функции у=х 2 +4х – 5
Так как нули функции это абсциссы точек пересечения ветвей параболы с осью х, то их координаты будут (х;0), то есть у=0. Значит, вместо у подставляем нуль в нашу формулу 0=х 2 +4х – 5 и получаем квадратное уравнение, решив которое, мы и найдем значения нулей функции:
D=b 2 – 4ac=4 2 – 4 ∙ 1 ∙ ( − 5 ) = 36
Значит, нули функции равны –5 и 1
Примечание к заданию по нахождению нулей функции без графика
Если дискриминант уравнения отрицательный, значит, нулей функции нет, то есть парабола не пересекает ось х (вершина находится выше неё, если ветви направлены вверх и ниже, если ветви направлены вниз).
Рассмотрим нахождение соответствия рисунков парабол, расположенных в системе координат значениям а и с.
Пример №3
Для выполнения данного задания на соответствие необходимо сначала поработать с графиками, подписав на них, какими – отрицательными или положительными являются коэффициенты а и с.
Теперь можно выполнить соответствие:
| А | Б | В |
| 2 | 3 | 1 |
Пример №4
Рассмотрим еще пример на соответствие
В данном задании рассмотрим коэффициенты в формулах и подчеркнем их: так, в формуле под буквой А коэффициент а=-2, т.е. отрицательный, значит, ветви направлены вниз, а это график под номером 2. В формулах под буквами Б и В первые и третьи коэффициенты одинаковые, значит, сравнить по рисунку их невозможно, следовательно, будем сравнивать по расположению вершины (справа или слева от оси у), а именно х0.
Итак, найдем х0 для формулы «Б»:
х0= − b 2 a . . = − 4 2 ∙ 2 . . = − 4 4 . . = − 1
Видим, что х0 отрицательное, значит, вершина расположена слева от оси у, а это рисунок 3. Ну и осталось привести в соответствие В и 1.
Запишем в таблицу
| А | Б | В |
| 2 | 3 | 1 |
А) a>0, с >0 Б) а 0 В) а>0, с
На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a 0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с 0, с >0 – это график №1
Б) а 0 – это график №3
pазбирался: Даниил Романович | обсудить разбор | оценить
Установите соответствие между функциями и их графиками.
ФУНКЦИИ
Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х 2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.
Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3
pазбирался: Даниил Романович | обсудить разбор | оценить
На рисунках изображены графики функций вида
Установите соответствие между знаками коэффициентов a и c и графиками функций.
Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида
Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a 0.
Далее мы смотрим, на что влияет коэффициент c.
Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:
если c > 0, то вершина параболы расположена выше оси х
Из всего вышеперечисленного можно найти ответ:
pазбирался: Даниил Романович | обсудить разбор | оценить
Видео:Координата вершины параболыСкачать

Найдите ординату вершины параболы которая задается уравнением y 3x 2 6x 5
Парабола проходит через точки A(0; 6), B(6; –6), C(1; 9). Найдите координаты её вершины.
Одна из возможных форм записи уравнения параболы в общем виде выглядит так: Координата x вершины параболы находится по формуле
Координату y вершины параболы найдётся подстановкой
в уравнение параболы. Таким образом, задача сводится к нахождению коэффициентов
и
Подставив координаты точек, через которые проходит парабола, в уравнение параболы и получим систему из трёх уравнений:
Найдём координаты вершины:
Парабола проходит через точки K(0; –5), L(4; 3), M(–3; 10). Найдите координаты её вершины.
Одна из возможных форм записи уравнения параболы в общем виде выглядит так: Координата x вершины параболы находится по формуле
Координату y вершины параболы найдётся подстановкой
в уравнение параболы. Таким образом, задача сводится к нахождению коэффициентов
и
Подставив координаты точек, через которые проходит парабола, в уравнение параболы и получим систему из трёх уравнений:
Найдём координаты вершины:
Переход от первой системы уравнений ко второй произведен путём умножения третьего уравнения на 4 и прибавления к нему второго уравнения, умноженного на 3.
Парабола проходит через точки K(0; –2), L(4; 6), M(1; 3). Найдите координаты её вершины.
Одна из возможных форм записи уравнения параболы в общем виде выглядит так: Координата x вершины параболы находится по формуле
Координату y вершины параболы найдётся подстановкой
в уравнение параболы. Таким образом, задача сводится к нахождению коэффициентов a, b и c. Подставим координаты точек, через которые проходит парабола, в уравнение параболы и получим систему из трёх уравнений:
Найдём координаты вершины:
Парабола проходит через точки K(0; 2), L( – 5; – 3), M(1; 9). Найдите координаты её вершины.
Одна из возможных форм записи уравнения параболы в общем виде выглядит так: Координата x вершины параболы находится по формуле
Координату y вершины параболы найдётся подстановкой
в уравнение параболы. Таким образом, задача сводится к нахождению коэффициентов
и
Подставив координаты точек, через которые проходит парабола, в уравнение параболы и получим систему из трёх уравнений:
Найдём координаты вершины:
Парабола проходит через точки A(0; – 6), B(1; – 9), C(6; 6). Найдите координаты её вершины.
Одна из возможных форм записи уравнения параболы в общем виде выглядит так: Координата x вершины параболы находится по формуле
Координату y вершины параболы найдётся подстановкой
в уравнение параболы. Таким образом, задача сводится к нахождению коэффициентов
и
Подставив координаты точек, через которые проходит парабола, в уравнение параболы и получим систему из трёх уравнений:
Найдём координаты вершины:
Парабола проходит через точки A(0; – 6), B( – 5; – 1), C(1; – 1). Найдите координаты её вершины.
Одна из возможных форм записи уравнения параболы в общем виде выглядит так: Координата x вершины параболы находится по формуле
Координату y вершины параболы найдётся подстановкой
в уравнение параболы. Таким образом, задача сводится к нахождению коэффициентов
и
Подставив координаты точек, через которые проходит парабола, в уравнение параболы и получим систему из трёх уравнений:
🔥 Видео
Как найти вершину параболы?Скачать

Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Квадратичная функция. Вершина параболы и нули функции. 8 класс.Скачать

Парабола. Квадратичная функцияСкачать

Вершина параболы | Квадратичная функция | Алгебра I (3 видео)Скачать

ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Квадратичная функция за 5 минутСкачать

Нахождение абсциссы вершины параболы. Математика 10-11 класс.Подготовка к ЕГЭ математика профиль.Скачать

Квадратичная функция и ее график. 8 класс.Скачать

№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать

Вершина параболы и ось симметрии. ПримерСкачать

Задание 23 из ОГЭ Построение графиков функций с модулем | МатематикаСкачать

Как легко составить уравнение параболы из графикаСкачать

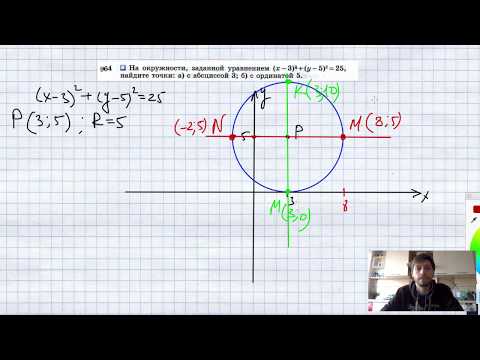
№964. На окружности, заданной уравнением (x-3)2 + + (y-5)2 = 25, найдите точки: а) с абсциссой 3;Скачать
Вершина параболы | Математика 9 класс | МегаШкола | Парабола | МегаШколаСкачать

Задание 11 (часть 1) | ЕГЭ 2024 Математика (профиль) | ГрафикиСкачать

Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Вариант 72, № 5. Уравнение оси симметрии параболы. Пример 2Скачать






