Найдите координаты точки пересечения прямых:
а ) x − y = − 1 и 2 x + y = 4 ;
б) 4 x + 3 y = 6 и 2 x + 3 y = 0 .
- ГДЗ учебник по алгебре 7 класс Мордкович. §7. Линейное уравнение с двумя переменными и его график. Номер №7.21.
- Решение а
- Пересекаются ли прямые 4y — 3x = — 17 и 4x + 3y = 6 если да, найди координаты из точек пересечения?
- Найдите координаты точек пересечения прямых y = 3 — x и y = 2x?
- Прямая у = х пересекает параболу у = х2 + 3х — 3?
- Даны прямые : у = 3х — 2 и у = 3 — 2х ?
- Найдите координаты точек пересечения прямых у = — х и у = х — 8?
- Найдите координаты точек пересечения прямых y = — x и y = 2x — 3?
- Найдите координаты точек пересечения прямой 0, 3x + 0, 2y = 6 с осями координат?
- Пересекаются ли парабола и прямая?
- Найдите координаты точек пересечения прямых заданных уравнениями у = 5х — 3 и у = 3х + 1?
- Найдите координаты точек пересечения прямой с осью х и осью у при у = — 1 / 3х + 1?
- Найдите координаты точек пересечения прямых y = — 1, 4x и x — y = 18?
- Точка пересечения прямых на плоскости онлайн
- Предупреждение
- Точка пересечения прямых на плоскости − теория, примеры и решения
- 1. Точка пересечения прямых, заданных в общем виде.
- 2. Точка пересечения прямых, заданных в каноническом виде.
- 3. Точка пересечения прямых, заданных в параметрическом виде.
- 4. Точка пересечения прямых, заданных в разных видах.
- 5. Примеры нахождения точки пересечения прямых на плоскости.
- 📹 Видео
Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

ГДЗ учебник по алгебре 7 класс Мордкович. §7. Линейное уравнение с двумя переменными и его график. Номер №7.21.
Решение а
x − y = − 1
−y = − 1 − x
y = x + 1
2 x + y = 4
2 x + x + 1 = 4
3 x = 4 − 1
3 x = 3
x = 1
y = x + 1
y = 1 + 1
y = 2
Ответ: точка пересечения прямых ( 1 ; 2 )
Видео:Выделение ФУНКЦИИ из уравнений прямых. Найти точку пересечения прямых, заданных уравнениямиСкачать

Пересекаются ли прямые 4y — 3x = — 17 и 4x + 3y = 6 если да, найди координаты из точек пересечения?
Алгебра | 5 — 9 классы
Пересекаются ли прямые 4y — 3x = — 17 и 4x + 3y = 6 если да, найди координаты из точек пересечения.
4(2 — 4 / 3 * x) — 3x + 17 = 0
8 — 16 / 3 * x — 3x + 17 = 0 — 25 / 3 * x = — 25
y = 2 — 4 / 3 * 3 = 2 — 4 = — 2
Видео:№976. Найдите координаты точки пересечения прямых 4x + 3y-6 = 0 и 2х+у-4 = 0.Скачать

Найдите координаты точек пересечения прямых y = 3 — x и y = 2x?
Найдите координаты точек пересечения прямых y = 3 — x и y = 2x.
Видео:ПЕРЕСЕЧЕНИЕ прямых | ТОЧКА пересечения | Линейные функцииСкачать

Прямая у = х пересекает параболу у = х2 + 3х — 3?
Прямая у = х пересекает параболу у = х2 + 3х — 3.
Найти координаты точек пересечения.
Видео:№975. Найдите координаты точек пересечения прямой 3x-4y + 12 = 0 с осями координатСкачать

Даны прямые : у = 3х — 2 и у = 3 — 2х ?
Даны прямые : у = 3х — 2 и у = 3 — 2х .
Найдите координаты точек пересечения прямых.
Видео:Не выполняя построения графиков, найдите координаты точки пересечения прямых. Алгебра 7 класс.Скачать

Найдите координаты точек пересечения прямых у = — х и у = х — 8?
Найдите координаты точек пересечения прямых у = — х и у = х — 8.
Видео:Нахождение координат точек пересечения графика функции с осями координатСкачать

Найдите координаты точек пересечения прямых y = — x и y = 2x — 3?
Найдите координаты точек пересечения прямых y = — x и y = 2x — 3.
Видео:Найти координаты точки пересечения прямыхСкачать
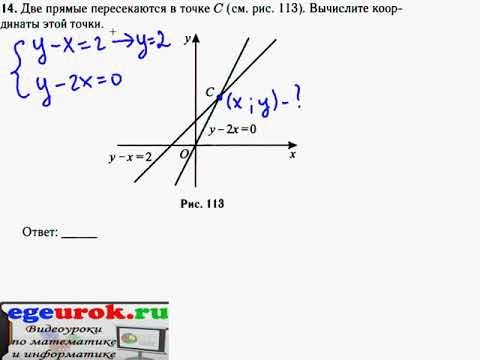
Найдите координаты точек пересечения прямой 0, 3x + 0, 2y = 6 с осями координат?
Найдите координаты точек пересечения прямой 0, 3x + 0, 2y = 6 с осями координат.
Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Пересекаются ли парабола и прямая?
Пересекаются ли парабола и прямая?
Если да, укажите координаты точек пересечения : y = x ^ 2 и x + y = 2.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Найдите координаты точек пересечения прямых заданных уравнениями у = 5х — 3 и у = 3х + 1?
Найдите координаты точек пересечения прямых заданных уравнениями у = 5х — 3 и у = 3х + 1.
Видео:Составляем уравнение прямой по точкамСкачать

Найдите координаты точек пересечения прямой с осью х и осью у при у = — 1 / 3х + 1?
Найдите координаты точек пересечения прямой с осью х и осью у при у = — 1 / 3х + 1.
Видео:Точки пересечения графиков линейных функций. 7 класс.ОбразовательныйСкачать

Найдите координаты точек пересечения прямых y = — 1, 4x и x — y = 18?
Найдите координаты точек пересечения прямых y = — 1, 4x и x — y = 18.
На этой странице сайта, в категории Алгебра размещен ответ на вопрос Пересекаются ли прямые 4y — 3x = — 17 и 4x + 3y = 6 если да, найди координаты из точек пересечения?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.
Это первое задание)))).
1) 100 * 3 = 300 км — пройденный путь шоссе 2) 60 * 2 = 120 км — пройденный путь грунтовая дорога 3) 300 + 120 = 420 км — весь пройденный путь 4) 3 + 2 = 5 часов — он ехал 5) 420 : 5 = 84 км / ч Ответ : средняя скорость автомобиля 84 км / ч.
1. а) 15в / с ^ 3 б) 5 (y — 2) * (y — 1) * (y + 1) / (y + 1) * (y — 2)(y + 2) = (5y — 5) / (y + 2) 2. (x — 3) ^ 2 * 4a ^ 2 / 8a ^ 3 * (x — 3)(x + 3) = (x — 3) / 2a (x + 3).
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Точка пересечения прямых на плоскости онлайн
С помощю этого онлайн калькулятора можно найти точку пересечения прямых на плоскости. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямых задайте вид уравнения прямых («канонический», «параметрический» или «общий»), введите коэффициенты уравнений прямых в ячейки и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Как построить график линейной функции.Скачать

Точка пересечения прямых на плоскости − теория, примеры и решения
- Содержание
- 1. Точка пересечения прямых, заданных в общем виде.
- 2. Точка пересечения прямых, заданных в каноническом виде.
- 3. Точка пересечения прямых, заданных в параметрическом виде.
- 4. Точка пересечения прямых, заданных в разных видах.
- 5. Примеры нахождения точки пересечения прямых на плоскости.
1. Точка пересечения прямых, заданных в общем виде.
Пусть задана декартова прямоугольная система координат Oxy и пусть в этой системе координат заданы прямые L1 и L2:
| L1: A1x+B1y+C1=0, | (1) |
| L2: A2x+B2y+C2=0 | (2) |
Для нахождения точки пересечения прямых (1) и (2) нужно решить систему линейных уравнений (1) и (2) относительно переменных x,y. Для этого запишем систему (1),(2) в матричном виде:
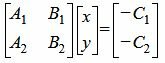 | (3) |
Построим расширенную матрицу:
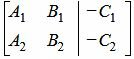 | (4) |
Приведем (4) к верхнему диагональному виду. Пусть A1≠0 . Тогда сложим строку 2 со строкой 1, умноженной на −A2/A1:
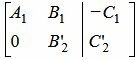 | (5) |
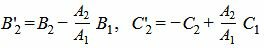 |
Если B’2=0 и С’2=0, то система линейных уравнений имеет множество решений. Следовательно прямые L1 и L2 совпадают. Если B’2=0 и С’2≠0, то система несовместна и, следовательно прямые параллельны и не имеют общей точки. Если же B’2≠0, то система линейных уравнений имеет единственное решение. Из второго уравнения находим y: y=С’2/B’2 и подставляя полученное значение в первое уравнение находим x: x=(−С1−B1y)/A1. Получили точку пересечения прямых L1 и L2: M(x, y).
Подробнее о решении систем линейных уравнений посмотрите на странице метод Гаусса онлайн.
2. Точка пересечения прямых, заданных в каноническом виде.
Пусть задана декартова прямоугольная система координат Oxy и пусть в этой системе координат заданы прямые L1 и L2:
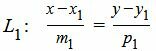 | (6) |
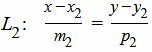 | (7) |
Приведем уравнение L1 к общему виду. Сделаем перекрестное умножение в уравнении (6):
| p1(x−x1)=m1(y−y1) |
Откроем скобки и сделаем преобразования:
| p1x−m1y−p1x1+m1y1=0 |
| A1x+B1y+C1=0 | (8) |
Аналогичным методом получим общее уравнение прямой (7):
| A2x+B2y+C2=0 | (9) |
Терерь можно найти точку пересечения прямых L1 и L2 методом, описанным в параграфе 1.
3. Точка пересечения прямых, заданных в параметрическом виде.
Пусть задана декартова прямоугольная система координат Oxy и пусть в этой системе координат заданы прямые L1 и L2 в параметрическом виде:
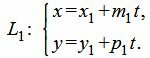 | (10) |
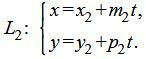 | (11) |
Приведем уравнение прямой L1 к каноническому виду. Для этого из уравнений (10) найдем параметр t:
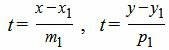 | (12) |
Из уравнений (12) следует:
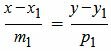 |
Аналогичным образом можно найти каноническое уравнение прямой L2:
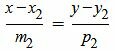 |
Как найти точку пересечения прямых, заданных в каноническом виде описано выше.
4. Точка пересечения прямых, заданных в разных видах.
Пусть задана декартова прямоугольная система координат Oxy и пусть в этой системе координат заданы прямые L1 и L2:
| L1: A1x+B1y+C1=0, | (13) |
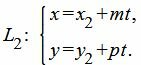 | (14) |
| A1(x2+mt)+B1(y2+pt)+C1=0, | (15) |
| A1x2+A1mt+B1y2+B1pt+C1=0, |
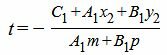 | (16) |
Если числитель и знаменатель в (16) одновременно равны нулю, то любое значение t удовлетворяет уравнению (15), следовательно прямые L1 и L2 совпадают. Если знаменатель равен нулю а числитель отличен от нуля, то прямые L1 и L2 не пересекаются, т.е. они параллельны.
Пусть знаменатель не равен нулю. Подставляя полученное значение t в (14), получим координаты точки пересечения прямых L1 и L2.
5. Примеры нахождения точки пересечения прямых на плоскости.
Пример 1. Найти точку пересечения прямых L1 и L2:
| L1: 2x+y+4=0, | (17) |
| L2: x−3y+2=0. | (18) |
Для нахождения точки пересечения прямых L1 и L2 нужно решить систему линейных уравнений (17) и (18). Представим уравнения в матричном виде:
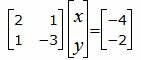 | (19) |
Решим систему линейных уравнений отностительно x, y. Для этого воспользуемся методом Гаусса. Получим:
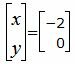 |
Ответ. Точка пересечения прямых L1 и L2 имеет следующие координаты:
Пример 2. Найти точку пересечения прямых L1 и L2:
| L1: 2x+3y+4=0, | (20) |
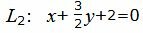 | (21) |
Для нахождения точки пересечения прямых L1 и L2 нужно решить систему линейных уравнений (20) и (21). Представим уравнения в матричном виде:
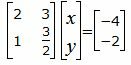 | (22) |
Для решения (22) воспользуемся методом Гаусса. Получим:
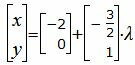 |
где λ− произвольное действительное число.
Имеем больше одного решения. Это означает, что прямые L1 и L2 совпадают.
Пример 3. Найти точку пересечения прямых L1 и L2:
| L1: −5x+y+9=0, | (23) |
| L2: −10x+2y−3=0, | (24) |
Для нахождения точки пересечения прямых L1 и L2 нужно решить систему линейных уравнений (23) и (24). Представим уравнения в матричном виде:
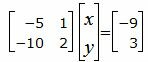 | (25) |
Применив метод Гаусса получим, что система (25) несовместна. Следовательно эти прямые не пересекаются, т.е. они параллельны.
Ответ. Прямые L1 и L2 не имеют общую точку, т.е. они параллельны.
Пример 4. Найти точку пересечения прямых L1 и L2:
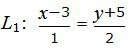 | (26) |
| L2: x+2y−9=0, | (27) |
Приведем, сначала, уравнение прямой (26) к общему виду:
Для нахождения точки пересечения прямых L1 и L2 нужно решить систему линейных уравнений (28) и (27). Представим уравнения в матричном виде:
 | (29) |
Решим систему линейных уравнений отностительно x, y:
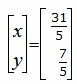 |
Ответ. Точка пересечения прямых L1 и L2 имеет следующие координаты:
📹 Видео
1.12.2. Линейная Функция | Сборник 1996-2007Скачать

9 класс, 7 урок, Уравнение прямойСкачать

Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Пересечения прямых, лучей, отрезковСкачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать








