Определение параболы. Параболой называется множество всех точек плоскости, таких, каждая из которых находится на одинаковом расстоянии от точки, называемой фокусом, и от прямой, называемой директрисой и не проходящей через фокус.
Каноническое уравнение параболы имеет вид:

где число p, называемое параметром параболы, есть расстояние от фокуса до директрисы.
На чертеже линия параболы — бордового цвета, директриса — ярко-красного цвета, расстояния от точки до фокуса и директрисы — оранжевого.
В математическом анализе принята другая запись уравнения параболы:
то есть ось параболы выбрана за ось координат. Можно заметить, что ax² — это квадратный трёхчлен ax² + bx + c , в котором b = 0 и c = 0 . График любого квадратного трёхчлена, то есть левой части квадратного уравнения, будет параболой.
Фокус параболы имеет координаты
Директриса параболы определяется уравнением 
Расстояние r от любой точки 

Для каждой из точек параболы расстояние до фокуса равно расстоянию до директрисы.
Пример 1. Определить координаты фокуса параболы
Решение. Число p расстояние от фокуса параболы до её директрисы. Начало координат в данном случае — в роли любой точки, расстояния от которой от фокуса до директрисы равны. Находим p:
Находим координаты фокуса параболы:
Пример 2. Составить уравнение директрисы параболы
Решение. Находим p:
Получаем уравнение директрисы параболы:
Пример 3. Составить уравнение параболы, если расстояние от фокуса до директрисы равно 2.
Решение. Параметр p — это и есть данное расстояние от фокуса до директрисы. Подставляем и получаем:
Траектория камня, брошенного под углом к горизонту, летящего футбольного мяча или артиллерийского снаряда будет параболой (при отсутствии сопротивления воздуха). Зона достижимости для пущенных камней вновь будет параболой. В данном случае речь идёт об огибающей кривой траекторий камней, выпущенных из данной точки под разными углами, но с одной и той же начальной скоростью.
Парабола обладает следующим оптическим свойством: все лучи, исходящие из источника света, находящегося в фокусе параболы, после отражения оказываются направленными параллельно её оси. Это свойство параболы используется при изготовлении прожекторов, автомобильных фар, карманных фонариков, зеркала которых имеют вид параболоидов вращения (фигур, получающихся при вращении параболы вокруг оси). Пучок параллельных лучей, двигающийся вдоль оси параболы, отражаясь, собирается в её фокусе.
- Задача 31453 Пожалуйста помогите 1)определить.
- Условие
- Решение
- Практическая работа по высшей математике на тему: «Парабола. Решение задач»
- Тема: «Кривые второго порядка. Парабола»
- Парабола, заданная квадратичной функцией
- Квадратичная функция при также является уравнением параболы и графически изображается той же параболой, что и но в отличие от последней имеет вершину не в начале координат, а в некоторой точке A, координаты которой вычисляются по формулам:
- Общее уравнение параболы
- В общем случае парабола не обязана иметь ось симметрии, параллельную одной из координатных осей. Однако, как и любое другое коническое сечение, парабола является кривой второго порядка и, следовательно, её уравнение на плоскости в декартовой системе координат может быть записано в виде квадратного многочлена:
- Краткое описание документа:
- 🎬 Видео
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Задача 31453 Пожалуйста помогите 1)определить.
Условие
Пожалуйста помогите
1)определить величину параметра расположение относительно координатных оси следующих парабол: y^2=6x x^2=5y
2)найти фокус и уравнение директрисы параболы y^2=24x
Решение
Канонические уравнения параболы:
x^2=2py cимметрична относительно оси Оу, ветви направлены в сторону оси Оу
Фокус F(0;p/2)
Уравнение директрисы:
y=-p/2
x^2=-2py cимметрична относительно оси Оу, ветви направлены в сторону противоположную оси Оу
Фокус F(0;-p/2)
Уравнение директрисы:
y= p/2
y^2=2px cимметрична относительно оси Ох, ветви направлены в сторону оси Ох
Фокус F(p/2;0)
Уравнение директрисы:
x=-p/2
y^2=-2px cимметрична относительно оси Ох, ветви направлены в сторону противоположную оси Ох
Фокус F(-p/2;0)
Уравнение директрисы:
x=p/2
[b]Решение[/b]:
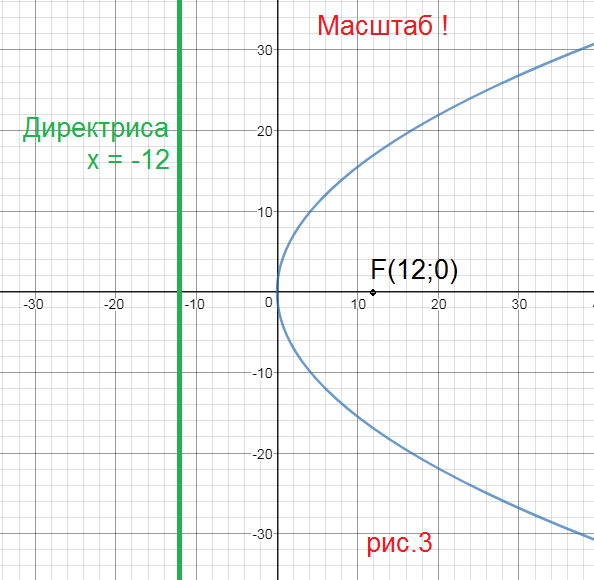
1) y^2=6x ⇒ 2p=6;
p=3
cимметрична относительно оси Ох, ветви направлены в сторону оси Ох
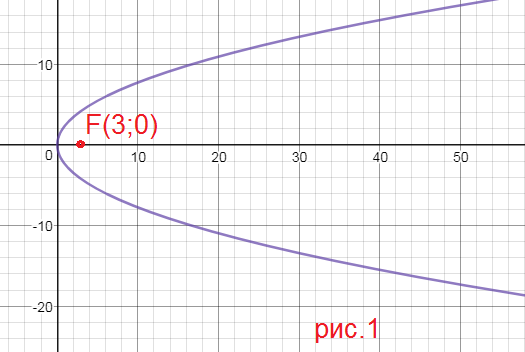
x^2=5y 2p=5 ⇒ 2p=5;
p=2,5
cимметрична относительно оси Оу, ветви направлены в сторону оси Оу
2)
y^2=24x ⇒ 2p=24;
p=12
cимметрична относительно оси Ох, ветви направлены в сторону оси Ох
Фокус F(12;0)
Уравнение директрисы:
x=-12
см. рис.3 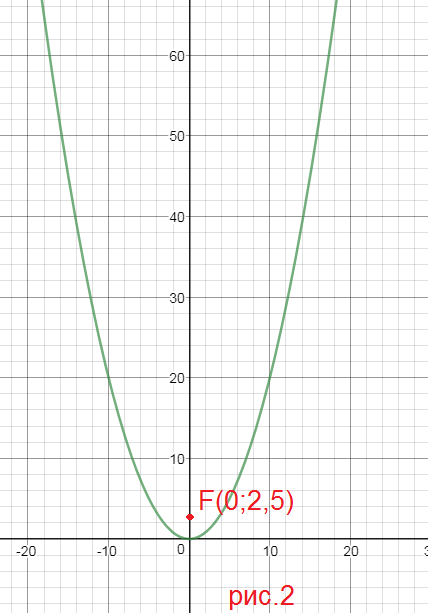
Видео:Как легко составить уравнение параболы из графикаСкачать

Практическая работа по высшей математике на тему: «Парабола. Решение задач»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 2 500 дидактических материалов для школьного и домашнего обучения
Дисциплина – «Элементы высшей математики»
Видео:213. Фокус и директриса параболы.Скачать

Тема: «Кривые второго порядка. Парабола»
Цель: формирование умений составлять уравнения параболы, исследовать форму и расположение параболы;
формирование общих компетенций, включающими в себя способность:
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
ОК 6. Работать в коллективе и в команде, эффективно общаться с коллегами, руководством, потребителями.
Методические указания и теоретические сведения к практической работе
Парабола — геометрическое место точек , равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).
Наряду с эллипсом и гиперболой , парабола является коническим сечением . Она может быть определена как коническое сечение с единичным эксцентриситетом .
Точка параболы, ближайшая к её директрисе, называется вершиной этой параболы. Вершина является серединой перпендикуляра, опущенного из фокуса на директрису.


Число p называется фокальным параметром, оно равно расстоянию от фокуса до директрисы. Поскольку каждая точка параболы равноудалена от фокуса и директрисы, то и вершина — тоже, поэтому она лежит между фокусом и директрисой на расстоянии 
Парабола, заданная квадратичной функцией
Квадратичная функция  при
при  также является уравнением параболы и графически изображается той же параболой, что и
также является уравнением параболы и графически изображается той же параболой, что и  но в отличие от последней имеет вершину не в начале координат, а в некоторой точке A, координаты которой вычисляются по формулам:
но в отличие от последней имеет вершину не в начале координат, а в некоторой точке A, координаты которой вычисляются по формулам:


Общее уравнение параболы
В общем случае парабола не обязана иметь ось симметрии, параллельную одной из координатных осей. Однако, как и любое другое коническое сечение, парабола является кривой второго порядка и, следовательно, её уравнение на плоскости в декартовой системе координат может быть записано в виде квадратного многочлена:
Если кривая второго порядка, заданная в таком виде, является параболой, то составленный из коэффициентов при старших членах дискриминант 
Пример 1. Найти координаты фокуса и уравнение директрисы параболы, заданной уравнением 
Решение. Из данного канонического уравнения параболы следует, что 




Пример 2. Составить каноническое уравнение параболы и уравнение ее директрисы, если известно, что вершина параболы лежит в начале координат, а фокус имеет координаты 
Решение. Согласно условию, фокус параболы расположен на отрицательной полуоси 
Так как 




Пример 3. Составить уравнение параболы, имеющей вершину в начале координат, симметричной оси Ох и проходящей через точку 
Решение. Из условия заключаем, что уравнение параболы следует искать в виде 
Так как точка 
Итак, уравнение параболы имеет вид 
Пример 4. Парабола симметрична относительно оси Ox , проходит через точку
A (4, -1), а вершина ее лежит в начале координат. Составить ее уравнение.
Решение. Так как парабола проходит через точку A (4, -1) с положительной абсциссой, а ее осью служит ось Ox , то уравнение параболы следует искать в виде y 2 = 2 px . Подставляя в это уравнение координаты точки A , будем иметь
искомым уравнением будет
Эскиз этой параболы показан на рисунке
Пример 5. Парабола y 2 = 2 px проходит через точку A (2, 4). Определить ее параметр p .
Решение. Подставляем в уравнение параболы вместо текущих координат координаты точки A (2, 4). Получаем
4 2 = 2 p *2; 16 = 4 p ; p = 4.
Пример 6. Привести к каноническому (простейшему) виду уравнение параболы
y = 2 x 2 + 4 x + 5 и найти координаты ее вершины.
Решение. Уравнение y = 2 x 2 + 4 x + 5 преобразуем, выделив в правой части полный квадрат:
пусть теперь x 1 = x + 1, y 1 = y — 3. Из сравнения с формулами
координаты нового начала: x 0 = -1; y 0 = 3. Уравнение параболы примет вид
Эскиз параболы показан на рисунке.
Пример 7. Упростить уравнение параболы y = x 2 — 7 x + 12, найти координаты ее вершины и начертить эскиз кривой.
Решение. Выделим в правой части уравнения y = x 2 — 7x + 12 полный квадрат по способу, указанному выше в задаче , и получим
Отсюда из сравнения с формулами
координаты нового начала, т. е. вершины параболы, будут 


Пример 8. Составить уравнение параболы и ее директрисы, если парабола проходит через точки пересечения прямой 


Решение. Найдем точки пересечения заданных линий, решив совместно их уравнения:
В результате получим два решения 









Итак, уравнением параболы будет 


Ответ. 
Пример 9. Мостовая арка имеет форму параболы. Определить параметр 

Решение. В ыберем прямоугольную систему координат так, чтобы вершина параболы (мостовой арки) находилась в начале координат, а ось симметрии совпадала с отрицательным направлением оси 





Ответ.
а) Найти координаты фокуса и уравнение директрисы параболы, заданной уравнением у 2 =16р .
б) Найти координаты фокуса и уравнение директрисы параболы, заданной уравнением
а) Составить каноническое уравнение параболы и уравнение ее директрисы, если известно, что вершина параболы лежит в начале координат, а фокус имеет координаты (0; -7).
б) Составить каноническое уравнение параболы и уравнение ее директрисы, если известно, что вершина параболы лежит в начале координат, а фокус имеет координаты (0; 4).
а) Составить уравнение параболы, имеющей вершину в начале координат, симметричной относительно оси Ох и проходящей через точку А (-2; — 4) . Начертить эскиз данной кривой.
б) Составить уравнение параболы, имеющей вершину в начале координат, симметричной относительно оси Ох и проходящей через точку А (3; — 5) . Начертить эскиз данной кривой.
а) Парабола y 2 = 2 px проходит через точку A (4; 8). Определить ее параметр p .
б) Парабола y 2 = — 2 px проходит через точку A (-4; -8). Определить ее параметр p .
а) Привести к каноническому (простейшему) виду уравнение параболы y = 2 x 2 + 8 x + 5 и найти координаты ее вершины. Начертить эскиз данной кривой.
б) Привести к каноническому (простейшему) виду уравнение параболы y = 4 x 2 + 16 x +10 и найти координаты ее вершины. Начертить эскиз данной кривой.
Задание 6. а) Составить уравнение параболы и ее директрисы, если парабола проходит через точки пересечения прямой 2х + 2у=0 и окружности х 2 +у 2 – 4х=0 и симметрична относительно оси Оу.
б) Составить уравнение параболы и ее директрисы, если парабола проходит через точки пересечения прямой 3х + 3у=0 и окружности 2х 2 + 2у 2 — 8х=0 и симметрична относительно оси Ох .
Задание 7. а) Арка здания имеет форму параболы. Определить параметр р этой параболы, зная, что пролет арки равен 12 м, а высота 4 м.
б) Арка дома имеет форму параболы. Определить параметр р этой параболы, зная, что пролет арки равен 14 м, а высота 6 м.
Отчет о практической работе
Тема практической работы
Цель практической работы
В ходе выполнения практической работы я научился (закрепил умения) вычислять…
Я получил (совершенствовал) практические навыки…
В ходе практической работы я получил новые знания. Узнал, что …
Мне было сложно выполнять…, потому, что…
Мне было несложно выполнять…, потому, что…
Краткое описание документа:
Практическая работа по высшей математике на тему: «Парабола. Решение задач». В работе представлены краткие теоретические сведения и методические указания для выполнения практической работы. Работа предназначена студентам 2 курса СПО. Может быть использована для аудиторной и внеаудиторной самостоятельной работы студентов 2 курса СПО.
🎬 Видео
Фокус и директриса параболы 2Скачать

Фокус и директриса параболы 1Скачать

КАК НАЙТИ ВЕРШИНУ ПАРАБОЛЫСкачать

Видеоурок "Парабола"Скачать

Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Квадратичная функция. Вершина параболы и нули функции. 8 класс.Скачать

Кривые второго порядка. Парабола. Приведение к каноническому виду и чертежСкачать

§24 Каноническое уравнение параболыСкачать

Построение параболы по ее директрисе и фокусуСкачать

ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Определение знаков коэффициентов квадратного уравнения (параболы) по рисунку/ЗНО 2010 #25Скачать

Как найти все коэффициенты параболы по графику? Большой ответ на этот вопрос.Скачать

Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать

Видеоурок "Гипербола"Скачать

Фокус и директриса параболы 2Скачать

Фокус и директриса параболы 2Скачать

Парабола (часть 1). Каноническое уравнение параболы. Высшая математика.Скачать











 при
при  также является уравнением параболы и графически изображается той же параболой, что и
также является уравнением параболы и графически изображается той же параболой, что и  но в отличие от последней имеет вершину не в начале координат, а в некоторой точке A, координаты которой вычисляются по формулам:
но в отличие от последней имеет вершину не в начале координат, а в некоторой точке A, координаты которой вычисляются по формулам:

































