Видео:Уравнение состояния идеального газа. Практическая часть. 10 класс.Скачать
Уравнение состояния идеального газа (уравнение Менделеева – Клапейрона). Изопроцессы
Состояние данной массы газа полностью определено, если известны его давление, температура и объем. Эти величины называют параметрами состояния газа. Уравнение, связывающее параметры состояния, называют уравнением состояния.
Для произвольной массы газа состояние газа описывается уравнением Менделеева—Клапейрона: pV = mRT/M, где р — давление, V — объем, m — масса, М — молярная масса, R — универсальная газовая постоянная. Физический смысл универсальной газовой постоянной в том, что она показывает, какую работу совершает один моль идеального газа при изобарном расширении при нагревании на 1 К (R = 8,31 ДжДмоль • К)).
Уравнение Менделеева—Клапейрона показывает, что возможно одновременное изменение трех параметров, характеризующих состояние идеального газа. Однако многие процессы в газах, происходящие в природе и осуществляемые в технике, можно рассматривать приближенно как процессы, в которых изменяются лишь два параметра. Особую роль в физике и технике играют три процесса: изотермический, изохорный и изобарный.
Изопроцессом называют процесс, происходящий с данной массой газа при одном постоянном параметре — температуре, давлении или объеме. Из уравнения состояния как частные случаи получаются законы для изопроцессов.
Изотермическим называют процесс, протекающий при постоянной температуре. Т = const. Он описывается законом Бойля—Мариотта: pV = const.
Изохорным называют процесс, протекающий при постоянном объеме. Для него справедлив закон Шарля: V = const, p/T = const.
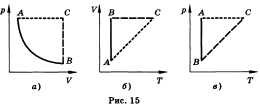
Изобарным называют процесс, протекающий при постоянном давлении. Уравнение этого процесса имеет вид V/T = const прир = const и называется законом Гей-Люссака. Все процессы можно изобразить графически (рис. 15).
Реальные газы удовлетворяют уравнению состояния идеального газа при не слишком высоких давлениях (пока собственный объем молекул пренебрежительно мал по сравнению с объемом сосуда,
в котором находится газ) и при не слишком низких температурах (пока потенциальной энергией межмолекулярного взаимодействия можно пренебречь по сравнению с кинетической энергией теплового движения молекул), т. е. для реального газа это уравнение и его следствия являются хорошим приближением.
Видео:Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать
Универсальное уравнение состояния идеального газа.
Идеальным газом называется такой газ, у которого отсутствуют силы взаимного притяжения и отталкивания между молекулами и пренебрегают размерами молекул. Все реальные газы при высоких температурах и малых давлениях можно практически считать как идеальные газы.
Уравнение состояния как для идеальных, как и для реальных газов описываются тремя параметрами по уравнению (1.7).
Уравнение состояния идеального газа можно вывести из молекулярно-кинетической теории или из совместного рассмотрения законов Бойля-Мариотта и Гей-Люссака.
Это уравнение было выведено в 1834 г. французким физиком Клапейроном и для 1 кг массы газа имеет вид:
где: R — газовая постоянная и представляет работу 1 кг газа в процессе при постоянном давлении и при изменении температуры на 1 градус.
Уравнение (2.7) называют термическим уравнением состояния или характеристическим уравнением.
Для произвольного количества газа массой m уравнение состояния будет:
В 1874 г. Д.И.Менделеев основываясь на законе Дальтона («В равных объемах разных идеальных газов, находящихся при одинаковых температурах и давлениях, содержится одинаковое количество молекул») предложил универсальное уравнение состояния для 1 кг газа, которую называют уравнением Клапейрона-Менделеева:
где: μ — молярная (молекулярная) масса газа, (кг/кмоль);
Rμ = 8314,20 Дж/кмоль (8,3142 кДж/кмоль) — универсальная газовая постоянная и представляет работу 1 кмоль идеального газа в процессе при постоянном давлении и при изменении температуры на 1 градус.
Зная Rμ можно найти газовую постоянную R = Rμ/μ.
Для произвольной массы газа уравнение Клапейрона-Менделеева будет иметь вид:
Смесь идеальных газов.
Газовой смесью понимается смесь отдельных газов, вступающих между собой ни в какие химические реакции. Каждый газ (компонент) в смеси независимо от других газов полностью сохраняет все свои свойства и ведет себя так, как если бы он один занимал весь объем смеси.
Парциальное давление – это давление, которое имел бы каждый газ, входящий в состав смеси, если бы этот газ находился один в том же количестве, в том же оюъеме и при той же температуре, что и в смеси.
Газовая смесь подчиняется закону Дальтона:
║Общее давление смеси газов равно сумме парциальных давлений ║отдельных газов, составляющих смесь.
где Р1 , Р2 , Р3 . . . Рn – парциальные давления.
Состав смеси задается объемными, массовыми и мольными долями, которые определяются соответственно по следующим формулам:
где V1 ; V2 ; … Vn ; Vсм –объемы компонентов и смеси;
m1 ; m2 ; … mn ; mсм – массы компонентов и смеси;
ν1 ; ν2 ; … νn ; νсм – количество вещества (киломолей)
компонентов и смеси.
Для идеального газа по закону Дальтона:
Связь между объемными и массовыми долями следующее:
где: μ1 , μ2 , … μn , μсм – молекулярные массы компонентов и смеси.
Молекулярная масса смеси:
Газовая постоянная смеси:
Удельные массовые теплоемкости смеси:
Удельные молярные (молекулярные) теплоемкости смеси:
Тема 3. Второй закон термодинамики.
Основные положения второго закона термодинамики.
Первый закон термодинамики утверждает, что теплота может превращаться в работу, а работа в теплоту и не устанавливает условий, при которых возможны эти превращения.
Превращение работы в теплоту происходит всегда полностью и безусловно. Обратный процесс превращения теплоты в работу при непрерывном её переходе возможен только при определенных условиях и не полностью. Теплота сам собой может переходит от более нагретых тел к холодным. Переход теплоты от холодных тел к нагретым сам собой не происходит. Для этого нужно затратить дополнительную энергию.
Таким образом для полного анализа явления и процессов необходимо иметь кроме первого закона термодинамики еще дополнительную закономерность. Этим законом является второй закон термодинамики. Он устанавливает, возможен или невозможен тот или иной процесс, в каком направлении протекает процесс, когда достигается термодинамическое равновесие и при каких условиях можно получить максимальную работу.
Формулировки второго закона термодинамики.
Для существования теплового двигателя необходимы 2 источника – горячий источник и холодный источник (окружающая среда). Если тепловой двигатель работает только от одного источника то он называется вечным двигателем 2-го рода.
1 формулировка (Оствальда):
| «Вечный двигатель 2-го рода невозможен».
Вечный двигатель 1-го рода это тепловой двигатель, у которого L>Q1, где Q1 — подведенная теплота. Первый закон термодинамики «позволяет» возможность создать тепловой двигатель полностью превращающий подведенную теплоту Q1в работу L, т.е. L = Q1. Второй закон накладывает более жесткие ограничения и утверждает, что работа должна быть меньше подведенной теплоты (L 0), то системе подводится тепло.
Если энтропия системы уменьшается (Ds ht . (3.10)
Тема 4. Термодинамические процессы.
Видео:Уравнение состояния идеального газа. 10 класс.Скачать
2.5. Универсальное уравнение состояния идеального газа
Идеальным газом называется такой газ, у которого отсутствуют силы взаимного притяжения и отталкивания между молекулами и пренебрегают размерами молекул. Все реальные газы при высоких температурах и малых давлениях можно практически считать как идеальные газы.
Уравнение состояния как для идеальных, как и для реальных газов описываются тремя параметрами по уравнению (1.7).
Уравнение состояния идеального газа можно вывести из молекулярно-кинетической теории или из совместного рассмотрения законов Бойля-Мариотта и Гей-Люссака.
Это уравнение было выведено в 1834 г. французким физиком Клапейроном и для 1 кг массы газа имеет вид:Р·υ = R·Т , (2.10)где: R — газовая постоянная и представляет работу 1 кг газа в процессе при постоянном давлении и при изменении температуры на 1 градус.
Уравнение (2.7) называют термическим уравнением состояния или характеристическим уравнением.
Для произвольного количества газа массой m уравнение состояния будет:Р·V = m·R·Т . (2.11)В 1874 г. Д.И.Менделеев основываясь на законе Дальтона («В равных объемах разных идеальных газов, находящихся при одинаковых температурах и давлениях, содержится одинаковое количество молекул») предложил универсальное уравнение состояния для 1 кг газа, которую называют уравнением Клапейрона-Менделеева:Р·υ = Rμ·Т/μ , (2.12)где: μ — молярная (молекулярная) масса газа, (кг/кмоль);Rμ = 8314,20 Дж/кмоль (8,3142 кДж/кмоль) — универсальная газовая постоянная и представляет работу 1 кмоль идеального газа в процессе при постоянном давлении и при изменении температуры на 1 градус.
Для произвольной массы газа уравнение Клапейрона-Менделеева будет иметь вид:
📹 Видео
Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать
Урок 147. Задачи на основное уравнение МКТ идеального газаСкачать
Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать
ЕГЭ. Физика. Уравнение состояния идеального газа. ПрактикаСкачать
Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать
Физика. 10 класс. Уравнение состояния идеального газа /23.11.2020/Скачать
Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать
Физика 10 класс. Уравнение состояния идеального газа, уравнение МенделееваСкачать
Урок 157. Изопроцессы и их графики. Частные газовые законыСкачать
идеальный газ УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗАСкачать
ЕГЭ по физике. Теория #25. Идеальный газ. Уравнение состояния идеального газаСкачать
Решение задач на основное уравнение МКТ идеального газа | Физика 10 класс #29 | ИнфоурокСкачать
Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. Практическая часть.10 классСкачать
Физика 10 Идеальный газ Основное уравнение МКТ идеального газа Решение задачСкачать
Уравнение состояния идеального газаСкачать
