2.4.4. Нарисуйте в указанном прямоугольнике электрический узел, для которого согласно первому закону Кирхгофа составлено уравнение: I1 + I2 — I3 + I4 — I5— I6 = 0

| Дано: | Решение: |
| E1=36B Rг=0.5 Ом E2=30B Rб=0,2 Ом R1=1.5 Ом | E1+E2=I2(R+r)+I,r E1=I,R1 I1= 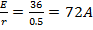 I2= I2= 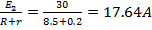 |
| Найти: | |
| Ответ: | 17.64A |
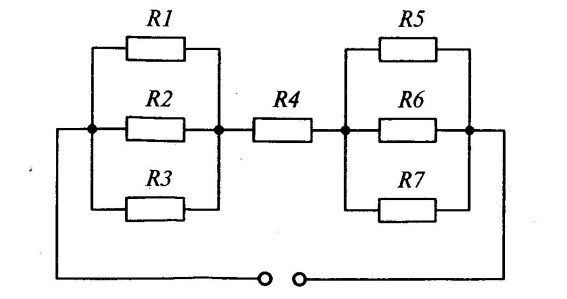
| Дано: | Решение: |
| R1=2 Ом R2=6 Ом R3=18 Ом R4=10 Ом R5=3 Ом R6=9 Ом R7=27 Ом | 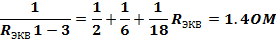 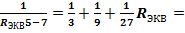 2.08OM 2.08OM  1,4+10+2,08=13,48 OM IОБЩ= 1,4+10+2,08=13,48 OM IОБЩ= 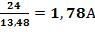 U4=10*1.78=17.8A U4=10*1.78=17.8A |
| Найти: | |
| U4 — ? | |
| Ответ: | 17.8A |
2.4.8. Напряжение сети 12 В. Общий ток, потребляемый четырьмя параллельно включенными одинаковыми лампами, равен 6 А. Определите сопротивление каждой лампы.
| Дано: | Решение: |
| U=12B I=6A |  RЭКВ= RЭКВ= 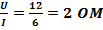 RЭКВ= RЭКВ=  R= RЭКВ*r R=2*4=8 OM-1лампа R= RЭКВ*r R=2*4=8 OM-1лампа |
| Найти: | |
| RA — ? | |
| Ответ: | 8 Ом |
Имеется разветвление, состоящее из четырех параллельно включенных сопротивлений в 10, 5, 3 и 8 Ом. Ток, протекающий к точке разветвления, равен 20 А. Определите ток, протекающий по каждой ветви.
| Дано: | Решение: |
| R1=10 Ом R2=5 Ом R3=3 Ом R4=8 Ом I=20A |  U=I*R=20*1.32=26.4B I1= U=I*R=20*1.32=26.4B I1=  I2= I2= 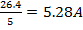 I3= I3= 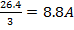 I4= I4=  |
| Найти: | |
| I1-I4 — ? | |
| Ответ: | I1=2.64A, I2=5.28A, I3=8.8A, I4=3.3A |
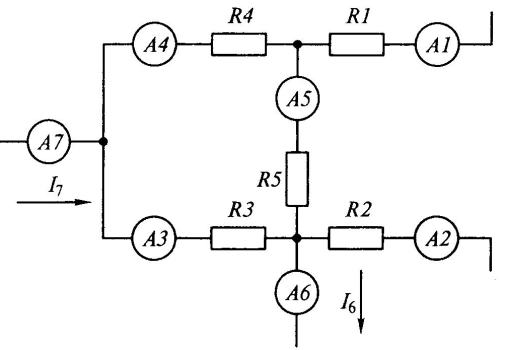
| Дано: | Решение: |
| A7=10A A1=8A A6=1A A5=0A | По закону Кирхгова I4=I1+I5 I4=I1=8A I3=I2+I1+I6 I3=2 I2=1 |
| Найти: | |
| I — ? | |
| Ответ: | I2=1; I3=2 |
2.4.11. Напряжение генератора 110 В. В сеть включены параллельно тридцать ламп сопротивлением по 200 Ом каждая. Определите ЭДС генератора, если его внутреннее сопротивление 0,5 Ом
| Дано: | Решение: |
| R=200 Ом r=0.5 Ом U=110B | I  RЭКВ= RЭКВ= 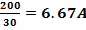 I= I= 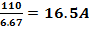 I= I=  |
| Найти:E | |
| Ответ: | 118.3B |
РАБОТА И МОЩНОСТЬ ЭЛЕКТРИЧЕСКОГО ТОКА
2.5.1. Заполните таблицу:
| 55кВт | 1500Вт | 1,5 МВт | 0,33 кВт | 0,12 МВт | 312 кВт |
| 5.5*10 4 Вт | 1.5 кВт | 1.5*10 3 кВт | 330 Вт | 1.2*10 2 кВт | 0.312 МВт |
2.5.2. Определите мощность, потребляемую электрическим двигателем, если ток в цепи равен 6 А, а двигатель включен в сеть напряжением 220 В.
| Дано: | Решение: |
| I=6A U=220B | P=UI P=220*6=1320BT |
| Найти: | |
| P — ? | |
| Ответ: | 1320BT |
На цоколе лампы накаливания написано: 200 Вт, 220 В. Определите сопротивление нити накаливания.
| Дано: | Решение: |
| P=200BT U=220B | P=UI; I= 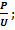 I= I= 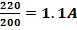 P=I 2 R R= P=I 2 R R= 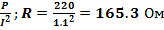 |
| Найти: | |
| R — ? | |
| Ответ: | 165.3 Ом |
2.5.5. Электродвигатель, подключенный к сети 220 В, потребляет ток в 6 А. Какова мощность двигателя и какое количество энергии он потребляет за 8 часов работы?
| Дано: | Решение: |
| U=220B I=6A | P=UI=220*6=1320BT=1.32КВТ/Ч W=PT=1.32*8=10.56КВТ/Ч |
| Найти: | |
| P,W — ? | |
| Ответ: | P=1.32кВт,W=10.56кВт/ч |
2.5.6. В квартире имеется восемь ламп, шесть из них мощностью по 40 Вт горят в сутки по 6 часов, а две мощностью по 60 Вт горят 8 часов в сутки. Сколько нужно заплатить за горение всех ламп в течении месяца (30 дней) при тарифе 120 руб. за 1 кВт час?
| Дано: | Решение: |
| P1-P6=40BT t1=6ч P7-P8=60BT t2=8ч | W=6*40*6+2*60*8=2.4КВТ/Ч WЧАС=2,4*30=72КВТ/Ч D=72*120=8640РУБ |
| Найти: | |
| W — ? | |
| Ответ: | 8640РУБ |
Глава 3 МАГНИТНЫЕ ЦЕПИ
МАГНИТНОЕ ПОЛЕ ТОКА И ЕГО ХАРАКТЕРИСТИКИ
3.1.1. В каких единицах системы СИ измеряются:
магнитная индукция В_ тесла (Тл)
магнитный поток Ф Вебер (Вб)
напряженность магнитного поля Н А/М
индуктивность L Генри (Гн)
3.1.2.Напишите формулы:
а) магнитной индукции б) магнитного потока
B= 
3.1.3. Закончите предложения:
Важное свойство магнитных линий— Замкнутость
Гистерезис — явление которое состоит в том, что физическая величина, характеризующая состояние тела (например, намагниченность) , неоднозначно зависит от физические величины, характеризующей внешние условия (например, магнитного поля)
Ферромагнетики — это вещество, в которых собственные ( внутреннее) магнитное поле может в сотни и тысячи раз превосходить вызывающее его магнитное поле.
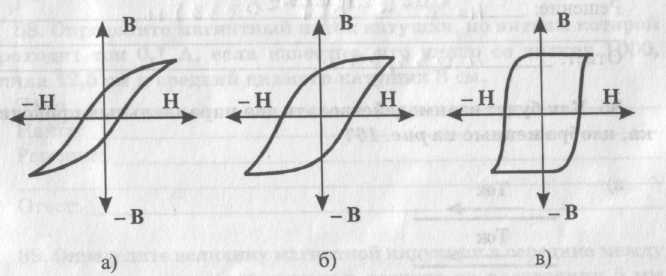
3.1.4. По виду гистерезисных кривых определите тип магнитного материала:
а) магнито- мягкий материал
б)магнито – твердый материал
3.1.5. Запишите формулу закона полного тока:
Что можно определить, применив правило левой руки?
Ответ: определения направления силы, действующей на проводник с током находящимся в магнитном поле.
3.1.7. Магнитная индукция стали 1,5 Тл, площадь поперечного сечения сердечника, изготовленного из этой стали, 0,003 м 2 . Определите магнитный поток, пронизывающий сердечник.
Последнее изменение этой страницы: 2016-04-11; Просмотров: 25611; Нарушение авторского права страницы
- Для цепи, изображенной на рисунке. Составить уравнения для определения токов путем непосредственного применения законов Кирхгофа. Решать эту систему уравнений не следует. Готовое решение: Заказ №7537
- Описание и исходные данные задания, 50% решения + фотография:
- Правила (законы) Кирхгофа простыми словами
- Первое правило Кирхгофа
- Второе правило Киргхофа
- Закон Кирхгофа для магнитной цепи
- Примеры расчета цепей
- 📽️ Видео
Видео:Законы Кирхгофа - самое простое и понятное объяснение этих законовСкачать

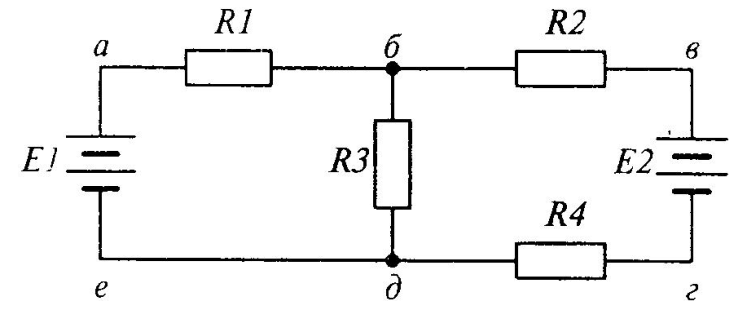
Для цепи, изображенной на рисунке. Составить уравнения для определения токов путем непосредственного применения законов Кирхгофа. Решать эту систему уравнений не следует. Готовое решение: Заказ №7537






Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.
Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!
Описание и исходные данные задания, 50% решения + фотография:
КОНТРОЛЬНАЯ РАБОТА № 1
ЗАДАЧА 3
Расчет разветвленной линейной цепи постоянного тока
с несколькими источниками электрической энергии
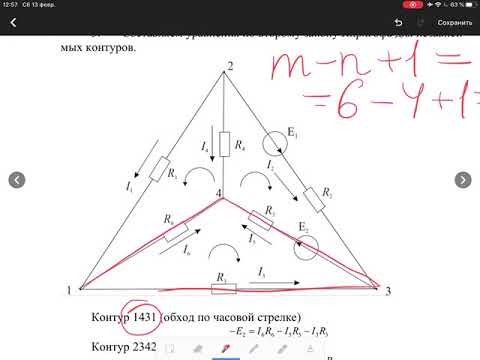
Для цепи, изображенной на рисунке:
1. Составить уравнения для определения токов путем непосредственного применения законов Кирхгофа. Решать эту систему уравнений не следует.
2. Определить токи в ветвях методом контурных токов.
3. Определить ток указанной ветви методом эквивалентного генератора.
4. Составить баланс мощностей.
5. Построить потенциальную диаграмму для контура, включающего две ЭДС.
E 1 =60 B, r 01 =0,5 Ом, E 2 =220 B, r 02 =0,5 Ом, r 1 =9 Ом, r 2 =3 Ом, r 3 =6 Ом, r 4 =5 Ом, r 5 =5 Ом, r 6 =8 Ом.
1. Уравнения по законам Кирхгофа.
Произвольно выберем и обозначим положительные направления токов ветвей, а также направления обхода независимых контуров.
Цепь содержит узла и ветвей. Необходимо определить 6 токов. Количество уравнений по 1-му закону ,
по 2-му закону Кирхгофа.
Я и моя команда оказывает помощь в учёбе по любым предметам и заданиям любой сложности.
Решение задач является неотъемлемой частью обучения в любом учебном заведении, и я смогу помочь в решение задач по любым предметам.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:Лекция 117. Правила КирхгофаСкачать

Правила (законы) Кирхгофа простыми словами
На практике часто встречаются задачи по расчётам параметров токов и напряжений в различных разветвлённых цепях. В качестве инструмента для расчётов используют правила Кирхгофа (в некоторой литературе их называют еще законами, хотя это не совсем корректно) – одни из фундаментальных правил, которые совместно с законами Ома позволяет определять параметры независимых контуров в самых сложных цепях.
Учёный Густав Киргхоф сформулировал два правила [1], для понимания которых введено понятие узла, ветви, контура. В нашей ситуации ветвью будем называть участок, по которому протекает один и тот же ток. Точки соединения ветвей образуют узлы. Ветви вместе с узлами образуют контуры – замкнутые пути, по которым течёт ток.
Видео:Урок 265. Задачи на правила КирхгофаСкачать

Первое правило Кирхгофа
Первое правило Густава Кирхгофа сформулировано исходя из закона сохранения заряда. Физик понимал, что заряд не может задерживаться в узле, а распределяется по ветвям контура, образующим это соединение.
Кирхгоф предположил, а впоследствии обосновал на основании экспериментов, что количество зарядов зашедших в узел такое же, как и количество тока вытекающего из него.
На рисунке 1 изображена простая схема, состоящая из контуров. Точками A, B, C, D обозначены узлы контура в центре схемы.
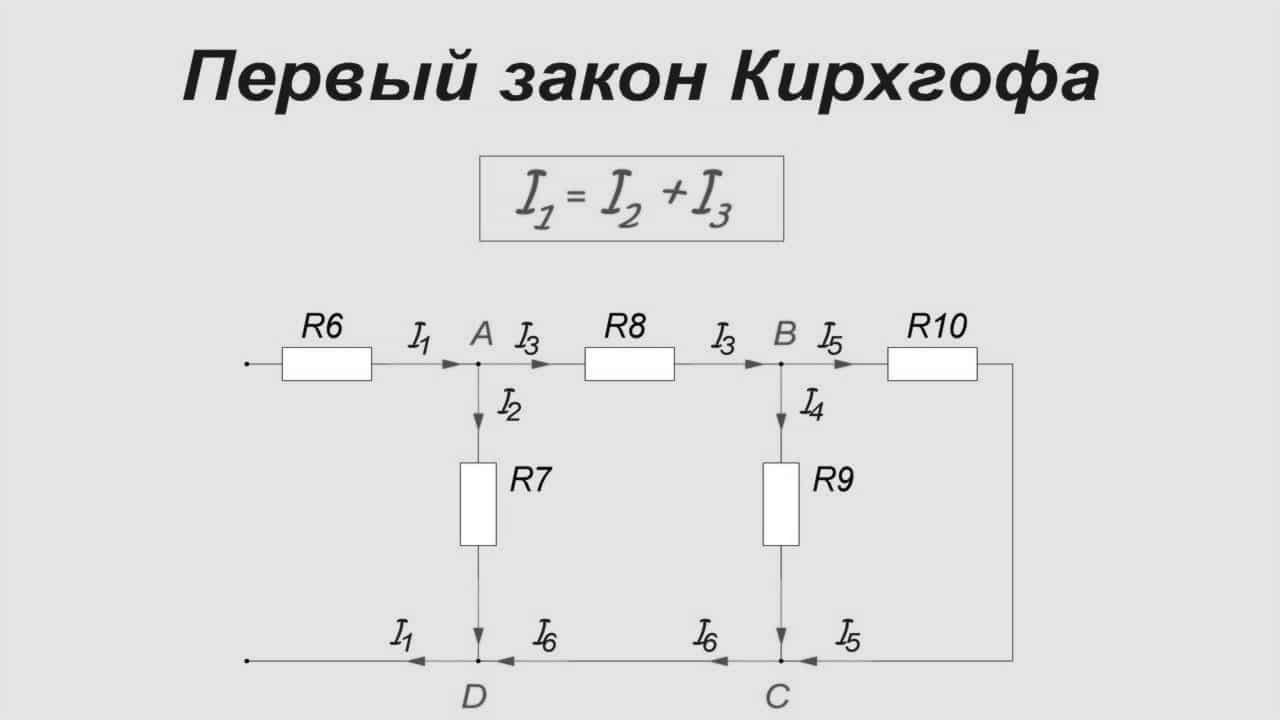
Ток I1 входит в узел A, образованный ветвями контура. На схеме электрический заряд распределяется в двух направлениях – по ветвям AB и AD. Согласно правилу Кирхгофа, входящий ток равен сумме выходящих: I1 = I2 + I3.
На рисунке 2 представлен абстрактный узел, по ветвям которого течёт ток в разных направлениях. Если сложить векторы i1, i2, i3, i4 то, согласно первому правилу Кирхгофа, векторная сумма будет равняться 0: i1 + i2 + i3 + i4 = 0. Ветвей может быть сколько угодно много, но равенство всегда будет справедливым, с учётом направления векторов.
Запишем наши выводы в алгебраической форме, для общего случая:
Для использования этой формулы, требуется учитывать знаки. Для этого необходимо выбрать направление одного из векторов тока (не важно, какого) и обозначить его знаком «плюс». При этом знаки всех других величин определить, исходя от их направления, по отношению к выбранному вектору.
Чтобы избежать путаницы, ток, направленный в точку узла, принято считать положительным, а векторы, направленные от узла – отрицательными.
Изложим первое правило Кирхгофа, выраженное приведённой выше формулой: «Алгебраическая сумма сходящихся в определённом узле токов, равна нулю, если считать входящие токи положительными, а отходящими – отрицательными».
Первое правило дополняет второе правило, сформулированное Кирхгофом. Перейдём к его рассмотрению.
Видео:Решение задачи. Расчет электрической цепи по законам КирхгофаСкачать

Второе правило Киргхофа
Из третьего уравнения Максвелла вытекает правило Кирхгофа для напряжений. Его ещё называют вторым законом.
Это правило гласит, что в замкнутом контуре, на резистивных элементах, алгебраическая сумма напряжений (включая внутренние), равна сумме ЭДС, присутствующих в этом же замкнутом контуре.
При этом токи и ЭДС, векторы которых совпадают с направлением (выбирается произвольно) обхода контура, считаются положительными, а встречные к обходу токи – отрицательными.

Формулы, которые изображены на рисунке применяются в частных случаях для вычисления параметров простых схем.
Формулировки уравнений общего характера:
, где где Lk и Ck – это индуктивности и ёмкости, соответственно.
Линейные уравнения справедливы как для линейных, так и для нелинейных линеаризованных цепей. Они применяются при любом характере временных изменений токов и напряжений, для разных источников ЭДС. При этом законы Кирхгофа справедливы и для магнитных цепей. Это позволяет выполнять вычисления для поиска соответствующие параметров.
Видео:Как составить уравнения по законам Кирхгофа?Скачать
Закон Кирхгофа для магнитной цепи
Применение независимых уравнений возможно и при расчётах магнитных цепей. Сформулированные выше правила Кирхгофа справедливы и для вычисления параметров магнитных потоков и намагничивающих сил.
То есть, для магнитных потоков первое правило Кирхгофа можно выразить словами: «Алгебраическая сумма всевозможных магнитных потоков относительно узла магнитной цепи равняется нулю.
Сформулируем второе правило для намагничивающих сил F: «В замкнутом магнитном контуре алгебраическая сумма намагничивающих сил приравнивается к сумме магнитных напряжений». Данное утверждение выражается формулой: ∑F=∑U или ∑Iω = ∑НL, где ω – количество витков, H – напряжённость магнитного поля, символ L обозначает длину средней линии магнитопровода. ( Условно принимается, что каждая точка этой линии совпадает с линиями магнитной индукции).
Второе правило, применяемое для вычисления магнитных цепей, есть не что иное, как альтернативная форма представления закона полного тока.
Примечание: Составляя уравнения с использованием формул, вытекающих из правил Кирхгофа, надо прежде определиться с положительным направлением потоков, функционирующих в ветвях, сопоставив их с направлением обходов существующих контуров.
При совпадении векторов магнитного потока с направлениями обхода (на некоторых участках), падение напряжения на этих ветвях берём со знаком « + », а встречные ему – со знаком « – ».
Видео:Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Примеры расчета цепей
Рассмотрим ещё раз рисунок 3. На нём изображено 4 разнонаправленных вектора: i1, i2, i3, i4. Из них – два входящие ( i2, i3) и два исходящие из узла (i1, i4). Положительными будем считать те векторы, которые направлены в точку соединения ветвей, а остальные – отрицательными.
Тогда, по формуле Кирхгофа, составим уравнение и запишем его в следующем виде: – i1 + i2 + i3 – i4 = 0.
На практике такие узлы являются частью контуров, обходя которые можно составить ещё несколько линейных уравнений с этими же неизвестными. Количество уравнений всегда достаточно для решения задачи.
Рассмотрим алгоритм решения на примере рис. 5.

Схема содержит 3 ветви и два узла, которые образуют три пары по два независимых контура:
Запишем независимое уравнение, выполняющееся, например, в точке а. Из первого правила Кирхгофа вытекает: I1 + I2 – I3 = 0.
Воспользуемся вторым правилом Кирхгофа. Для составления уравнений можно выбрать любой из контуров, но нам необходимы контуры с узлом а, так как для него мы уже составили уравнение. Это будут контуры 1 и 2.
Пишем уравнения:
Решаем систему уравнений:
Так как значения R и E известны (см. рисунок 5), мы придём к системе уравнений:
Решая эту систему, получим:
Потенциал узла а равен: Ua = I3*R3 = 3,55 × 3 = 10,65 В. Чтобы убедиться в верности наших расчётов, проверим выполнение второго правила по отношению к контуру 3:
E1 – E2 + I1R1+ I2R2 = 12 – 15 + 1,36 – 4,38 = – 0,02 ≈ 0 (с учётом погрешностей, связанных с округлениями чисел при вычислениях).
Если проверка выполнения второго правила успешно завершена, то расчёты сделаны правильно, а полученные данные являются достоверными.
Применяя правила (законы) Кирхгофа можно вычислять параметры электрической энергии для магнитных цепей.
📽️ Видео
решение задачи составлением уравнений по правилам киргофа. Законы киргофа кратко на практикеСкачать

Правило КирхгофаСкачать

Расчет цепи с ИСТОЧНИКОМ ТОКА по законам КирхгофаСкачать

Урок 263. Правила КирхгофаСкачать

Урок 14. Законы Кирхгофа простыми словами с примерамиСкачать

Метод контурных токов - определение токов. ЭлектротехникаСкачать

☠#8 Урок. Законы Кирхгофа - САМОЕ ПРОСТОЕ ОБЪЯСНЕНИЕ!Скачать

Применение законов Кирхгофа при решении задачСкачать

Расчет электрической цепи постоянного тока методом узловых и контурных уравненийСкачать
как решать задачи со сложными схемамиСкачать

Первый закон Кирхгофа! Хочешь понять? Посмотри!Скачать

ОЛИМПИАДНАЯ ФИЗИКА. Правила КирхгофаСкачать

Разветвленные цепи. Правила КирхгофаСкачать

Лекция 020-1. Цепи постоянного тока. Расчет при помощи уравнений КирхгофаСкачать