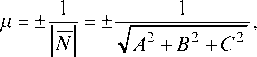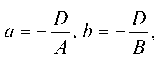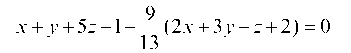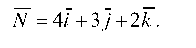С помощю этого онлайн калькулятора можно найти линию пересечения плоскостей. Дается подробное решение с пояснениями. Для нахождения уравнения линии пересечения плоскостей введите коэффициенты в уравнения плоскостей и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
- Предупреждение
- Линия пересечения плоскостей − теория, примеры и решения
- 1.3.2. Аналитическая геометрия в пространстве
- Напишите уравнение плоскости, проходящей через точку М (1; 1; 1) и перпендикулярной линии пересечения плоскостей 2x-y+z-l = 0 и x+y-2z-2 = 0.
- Ваш ответ
- решение вопроса
- Похожие вопросы
- 🔥 Видео
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать
Линия пересечения плоскостей − теория, примеры и решения
Две плоскости в пространстве могут быть параллельными, могут совпадать или пересекаться. В данной статье мы определим взаимное расположение двух плоскостей, и если эти плоскости пересекаются, выведем уравнение линии пересечения плоскостей.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы плоскости α1 и α2:
| α1: A1x+B1y+C1z+D1=0, | (1) |
| α2: A2x+B2y+C2z+D2=0, | (2) |
Найдем уравнение линии пересеченя плоскостей α1 и α2. Для этого рассмотрим следующие случаи:
 |
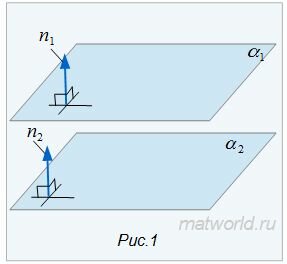Умножив уравнение (2) на λ, получим:
| α2: A1x+B1y+C1z+λD2=0, | (3) |
 |
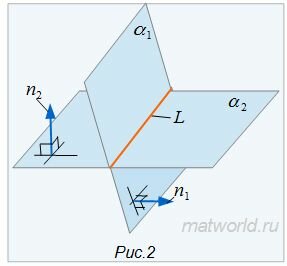Если векторы n1 и n2 не коллинеарны, то решим систему линейных уравнений (1) и (2). Для этого переведем свободные члены на правую сторону уравнений и составим соответствующее матричное уравнение:
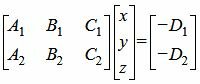 | (4) |
Как решить уравнение (4) посмотрите на странице Метод Гаусса онлайн или Метод Жоржана-Гаусса онлайн.
Так как в системе линейных уравнений (4) векторы n1=<A1, B1, C1> и n2=<A2, B2, C2> не коллинеарны, то решение этой системы линейных уравнений имеет следующий вид:
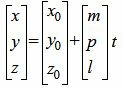 , | (5) |
Равенство (5) можно записать в следующем виде:
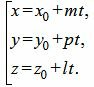 . | (6) |
Мы получили параметрическое уравнение прямой, которое является линией пересечения плоскостей α1 и α2. Полученное уравнение прямой можно записать в каноническом виде:
 . |
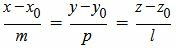Пример 1. Найти линию пересечения плоскостей α1 и α2:
| α1: x+2y+z+54=0. | (7) |
| α2: 2x+9y−5z+32=0. | (8) |
Поскольку направляющие векторы n1 и n2 неколлинеарны, то плолскости α1 и α2 пересекаются.
Для нахождения линии пересечения влоскостей α1 и α2 нужно решить систему линейных уравнений (7) и (8). Для этого составим матричное уравнение этой системы:
 . | (9) |
Решим систему линейных уравнений (9) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
 . | (10) |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строку 2 со строкой 1, умноженной на −2:
 . |
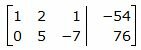Второй этап. Обратный ход Гаусса.
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на −2/5:
 . |
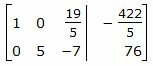Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
 . |
 . | (11) |
где t− произвольное действительное число.
Запишем (11) в следующем виде:
 . | (12) |
Получили уравнение линии пересечения плоскостей α1 и α2 в параметрическом виде. Запишем ее в каноническом виде.
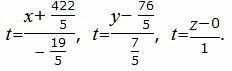 | (13) |
Из равентсв выше получим каноническое уравнение прямой:
 |
Ответ. Уравнение линии пересечения плоскостей α1 и α2имеет вид:
|
Пример 2. Найти линию пересечения плоскостей α1 и α2:
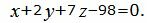 | (14) |
 | (15) |
Поскольку направляющие векторы n1 и n2 коллинеарны (n1 можно получить умножением n2 на число 1/2), то плоскости α1 и α2 параллельны или совпадают.
При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α2 умножив на число 1/2:
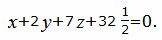 | (16) |
Так как нормальные векторы уравнений (14) и (16) совпадают, а свободные члены разные, то плоскости α1 и α2 не совпадают. Следовательно они параллельны, т.е. не пересекаются.
Пример 3. Найти линию пересечения плоскостей α1 и α2:
 | (17) |
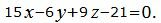 | (18) |
Поскольку направляющие векторы n1 и n2 коллинеарны (n1 можно получить умножением n2 на число 1/3), то плоскости α1 и α2 параллельны или совпадают.
При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α2 умножив на число 1/3:
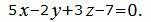 | (19) |
Так как нормальные векторы уравнений (17) и (19) совпадают, и свободные члены равны, то плоскости α1 и α2 совпадают.
Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать
1.3.2. Аналитическая геометрия в пространстве
1. Всякая плоскость в координатном пространстве OXYZ имеет векторное уравнение следующего вида: r ¦ п = p. Здесь
r = xi + yj + zk — радиус-вектор текущей точки плоскости
M(x, у, z); п = i cosa + j cos b + k cosg — единичный вектор, имеющий направление перпендикуляра, опущенного на плоскость из начала координат, a, b, g — углы, образованные этим перпендикуляром с осями координат OX, OY, OZ, и р — длина этого перпендикуляра.
При переходе к координатам это уравнение принимает вид xcos a + ycos b + zcos g — p = 0 (нормальное уравнение плоскости).
2. Уравнение всякой плоскости может быть записано также в виде Ах + Ву +Cz + D = 0 (общее уравнение). Здесь А, B, C можно рассматривать как координаты некоторого вектора
N = Ai + Bj + Ck, перпендикулярного к плоскости. Для приведения общего уравнения плоскости к нормальному виду все члены уравнения надо умножить на нормирующий множитель
где знак перед радикалом противоположен знаку свободного члена D в общем уравнении плоскости.
3. Частные случаи расположения плоскости, определяемой уравнением Ах + Ву +Cz + D = 0:
А = 0; плоскость параллельна оси ОХ;
В = 0; плоскость параллельна оси О^
C = 0; плоскость параллельна оси ОZ;
D = 0; плоскость проходит через начало координат;
А = В = 0; плоскость перпендикулярна оси ОZ (параллельна плоскости ХОY);
А = C = 0; плоскость перпендикулярна оси ОY (параллельна плоскости ХОZ);
В = C = 0; плоскость перпендикулярна оси ОХ (параллельна плоскости YОZ);
А = D = 0; плоскость проходит через ось ОХ;
В = D = 0; плоскость проходит через ось OY;
C = D = 0; плоскость проходит через ось OZ;
А = В = D = 0; плоскость совпадает с плоскостью XOY (z = 0);
А = C = D = 0; плоскость совпадает с плоскостью XOZ (у = 0);
B = C = D = 0; плоскость совпадает с плоскостью YOZ (х = 0).
Если в общем уравнении Ах + By +Cz + D = 0 коэффициент D ф 0, то, разделив все члены уравнения на — D, можно уравнение
плоскости привести к виду
^ здесь
. Это уравнение плоскости называется уравнением в отрезках: в нем а — абсцисса точки пересечения плоскости с осью OX, b и с — соответственно ордината и аппликата точек пересечения плоскости с осями OY и OZ.
4. Угол j между плоскостями А1х + В1У + Qz + D1 = 0 и А2х + В2У +C2z + D2 = 0 определяется по формуле
Условие параллельности плоскостей:
Условие перпендикулярности плоскостей:
5. Расстояние от точки М0(х0; у0; z0) до плоскости, определяемой уравнением
Находится по формуле
Оно равно взятому по абсолютной величине результату подстановки координат точки в нормальное уравнение плоскости; знак результата этой подстановки характеризует взаимное расположение точки M0 и начала координат относительно данной плоскости: этот знак положителен, если точка M0 и начало координат расположены по разные стороны от плоскости, и отрицателен, если они расположены по одну сторону от плоскости.
6. Уравнение плоскости, проходящей через точку М0(х0; у0; z0)
и перпендикулярной к вектору N = Ai + Bj + Ck, имеет вид А(х — х0) + B(y — у0) + C(z — z0) = 0. При произвольных А, В и C последнее уравнение определяет некоторую плоскость, принадлежащую к связке плоскостей, проходящих через точку М0. Его часто поэтому называют уравнением связки плоскостей.
7. Уравнение А1х + B1y +C1z + D1 + А(А2х + B^y +C2z + D2) = 0 при произвольном I определяет некоторую плоскость, проходящую через прямую, по которой пересекаются плоскости, определяемые уравнениями
некоторую плоскость, принадлежащую пучку плоскостей, проходящих через эту прямую (в силу чего такое уравнение часто называют уравнением пучка плоскостей). Если плоскости, определяемые уравнениями I и II, параллельны, то пучок плоскостей превращается в совокупность плоскостей, параллельных этим плоскостям.
8. Уравнение плоскости, проходящей через три заданные точки M1(r 1Х M1(Jj), M3(r 3) (Л = x1i + yd + z1k; r2 = x2i + У2 j + z2k; r3 = x3i + y3 j + z3 к), проще всего найти из условия компланарности векторов r — T1, r2 — rl, r3 — rl, где r = xi + yj+zk — радиус-вектор текущей точки искомой плоскости M:
или в координатной форме:
Пример 1.21. Составить уравнение плоскости, проходящей через линию пересечения плоскостей x + у + 5z — 1 = 0, 2x + 3у — z + 2 = 0 и через точку М(3, 2, 1).
Решение. Воспользуемся уравнением пучка плоскостей
Значение I определяем из условия, что координаты точки М должны удовлетворять этому уравнению:
Получаем искомое уравнение в виде:
или, умножая на 13 и приводя подобные члены, в виде:
Пример 1.22. Составить уравнение плоскости, проходящей через линию пересечения плоскостей x + 3у + 5z — 4 = 0 и X — у — 2z + 7 = 0 и параллельной оси оу.
Решение. Воспользуемся уравнением пучка x + 3у + 5z — 4 + + l(x — у — 2z + 7) = 0, преобразуем уравнение к виду (1 + Х)х + (3 -1)у + (5 — 2l)z + (71 — 4) = 0.
Так как искомая плоскость параллельна оси ординат, то коэффициент при у должен равняться нулю, т. е. 3 — l = 0, I = 3. Подставив значение I в уравнение пучка, получаем
Пример 1.23. Найти уравнение плоскости, проходящей через точки М (2; -1; 4) и N(3; 2; -1) перпендикулярно к плоскости X + у + z — 3 = 0.
Решение. Воспользуемся уравнением плоскости, проходящей через первую из данных точек:
Условие прохождения этой плоскости через вторую точку и условие перпендикулярности определяются равенствами:
Исключая коэффициенты А, В и C из системы уравнений
получаем искомое уравнение в виде:
Пример 1.24. Из точки P(2; 3; -5) на координатные плоскости опущены перпендикуляры. Найти уравнение плоскости, проходящей через их основания.
Решение. Основаниями перпендикуляров, опущенных на координатные плоскости, будут следующие точки М1(2; 3; 0), М2(2; 0; -5), М3(0; 3; -5). Напишем уравнение плоскости, проходящей через точки М1, М2, М3, для чего воспользуемся уравнением
Пример 1.25. Составить уравнение плоскости, проходящей через точку M (2; 3; 5) и перпендикулярной к вектору
Решение. Достаточно воспользоваться уравнением плоскости, проходящей через данную точку и перпендикулярной к данному вектору:
1. Прямая может быть задана уравнениями 2-х плоскостей
пересекающихся по этой прямой.
2. Исключив поочередно х и у из предыдущих уравнений, получим уравнения х = аz + с, у = bz + d. Здесь прямая определена двумя плоскостями, проектирующими ее на плоскости хoz и yoz.
3. Если даны две точки M(x1, у1, z1) и N(x2, у2, z2), то уравнения прямой, проходящей через них, будут иметь вид:
4. Так называемые канонические уравнения
определяют прямую, проходящую через точку M(x1, у1, z1)
и параллельную вектору S = li + mj + nk. В частности, эти уравнения могут быть записаны в виде:
где a, b и g — углы, образованные прямой с осями координат.
5. От канонических уравнений прямой, вводя параметр t, нетрудно перейти к параметрическим уравнениям прямой:
6. Угол между двумя прямыми, заданными их каноническими
деляется по формуле
перпендикулярности двух прямых:
условие параллельности двух прямых:
7. Необходимое и достаточное условие расположения двух прямых, заданных их каноническими уравнениями, в одной плоскости (условие компланарности двух прямых):
Если величины /1, т, П1 непропорциональны величинам /2, m2, «2, то указанное соотношение является необходимым и достаточным условием пересечения двух прямых в пространстве.
условие параллельности прямой и плоскости: 
условие перпендикулярности прямой и плоскости:
Определяется по формуле
9. Для определения точки пересечения прямой
С плоскостью Ах + Ву + Cz + D = 0 нужно решить совместно их уравнения, для чего следует воспользоваться параметрическими уравнениями прямой x = /t + X0, у = mt + у0, z = nt + z0:
а) если А/ + Вт + Cn ф 0, то прямая пересекает плоскость в одной точке;
б) если А/ + Вт + Cn = 0 и Ах0 + Ву0 + Cz0 + D ф 0, то прямая параллельна плоскости;
в) если А/ + Вт + Cn = 0 и Ах0 + Ву0 + Cz0 + D = 0, то прямая лежит в плоскости.
Пример 1.26. Привести к каноническому виду уравнения прямой 2х — у + 3z — 1 = 0 и 5х + 4у — z — 7 = 0.
Решение. Исключив вначале у, а затем z, получим:
Если разрешим каждое из уравнений относительно х, то будем иметь:
отсюда
Второй способ: найдем вектор S = li + mj + nk, параллельный искомой прямой. Так как он должен быть перпендикулярен к нормальным векторам заданных плоскостей N1 = 2i — j + 3k и N2= 5i + 4 j — k, то за него можно принять векторное произведение векторов N1 и N2.
Таким образом, l = -11; m = 17; n = 13.
За точку M1(x1, у1, z1), через которую проходит искомая прямая, можно принять точку пересечения ее с любой из координатных плоскостей, например с плоскостью yoz. Т ак как при этом x1 = 0, то координаты y1 и z1 этой точки определятся из системы уравнений заданных плоскостей, если в них положить х = 0:
Решая эту систему, находим у1 = 2; z1 = 1.
Итак, искомая прямая определяется уравнениями:
Мы получили прежний ответ.
Пример 1.27. Построить прямую
Решение. Искомую прямую можно построить как линию пересечения плоскостей. Для этого напишем уравнения плоскостей, которыми определена прямая, в отрезках на осях:
Пример 1.28. Из начала координат опустить перпендикуляр на прямую
Решение. Составим уравнение плоскости, проходящей через начало координат и перпендикулярной заданной прямой: 2х + 3у + z = 0. (Для этой плоскости можно принять А = l; B = m; C = n; D = 0; использовано условие перпендикулярности прямой и плоскости, см. п. 8 введения к настоящему разделу).
Найдем точку пересечения этой плоскости и данной прямой. Параметрические уравнения прямой имеют вид:
Построив данные плоскости, мы получим искомую прямую как линию пересечения этих плоскостей (рис. 20).
Для определения t имеем уравнение:
Остается составить уравнения прямой, проходящей через начало координат и через точку М (см. п. 3 введения к настоящему разделу):
Пример 1.29. В уравнениях прямой
Определить
параметр n так, чтобы эта прямая пересекалась с прямой
, и найти точку их пересечения.
Решение. Для нахождения параметра n используем условие пересечения 2-х прямых:
Следовательно, уравнения пересекающихся прямых таковы: искомой:
Для вычисления координат точки пересечения этих прямых выразим из первого уравнения х и у через z: х = 2z, у = -3z. Подставляя их значения в равенство
Имеем
,
отсюда z = 1. Зная z, находим х и у: х = 2z = 2, у = -3z = -3. Следовательно M(2; -3; 1).
Пример 1.30. Прямая задана каноническими уравнениями
Составить общие уравнения этой прямой.
Решение. Канонические уравнения прямой можно записать в виде системы двух независимых уравнений:
Получили общие уравнения прямой, которая теперь задана пересечением 2-х плоскостей, одна из которых 5х — 3у — 13 = 0 параллельна оси Oz, а другая х + 3z — 11 = 0 параллельна оси Oy.
Пример 1.31. Найти координаты точки M, делящей попалам отрезок прямой
заключенный между плоскостями хoz и xoy.
Решение. Найдем точку А пересечения прямой с плоскостью хoz, полагая в уравнениях прямой у = 0. Тогда получим:
отсюда x = 2,6; z = 2,8. Тогда А(2,6; 0; 2,8).
отсюда X = 11, у = 14, или В(11; 14; 0).
Определяем координаты точки М, делящей отрезок АВ пополам:
Следовательно, координаты искомой точки М будут: М(6,8; 7; 1,4).
Пример 1.32. Составить уравнение плоскости, проходящей через прямую
Решение. Составим уравнение пучка плоскостей, проходящих через первую из данных прямых:
которое делим на а ф 0, и пусть b /а = I:
Аналогично, полагая в уравнениях прямой z = 0, найдем координаты точки В пересечения прямой с плоскостью хоу:
В этом пучке нужно выбрать плоскость, параллельную 2-й данной прямой. Из условия параллельности плоскости и прямой, имеем:
Подставляя I = 1 в уравнение пучка плоскостей, получим: 
Тогда искомое уравнение плоскости будет:
Пример 1.33. Дана прямая 
Найти ее проекцию на плоскость
Решение. Нужно найти плоскость, которая проходит через данную прямую перпендикулярно к данной плоскости; тогда искомая проекция определится как пересечение этой плоскости с данной.
Составим уравнение пучка плоскостей, проходящих через данную прямую:
Эта плоскость должна быть перпендикулярной к данной плоскости, что можно записать как:
Тогда уравнение плоскости, проходящей через данную прямую и перпендикулярной данной плоскости, будет:
Проекция данной прямой на данную плоскость определяется как прямая пересечения плоскостей:
Запишем эту прямую в каноническом виде. Найдем на прямой какую-либо точку. Для этого положим, например х0 = 1, и система запишется в виде:
Отсюда, у0 = 1, z0 = 0, т. е. точка M(1; 1; 0) принадлежит искомой прямой.
Направляющий вектор прямой S = (l; m; n) найдем из того условия, что он перпендикулярен нормальным векторам
N1 = (2; -3; -2) и N2 = (5; 2; 2) плоскостей, определяющих искомую прямую.
В качестве S берем векторное произведение векторов N1 и N2 , т. е.
Тогда искомое уравнение в каноническом виде будет:
Видео:10. Параллельность и перпендикулярность плоскостей Решение задачСкачать
Напишите уравнение плоскости, проходящей через точку М (1; 1; 1) и перпендикулярной линии пересечения плоскостей 2x-y+z-l = 0 и x+y-2z-2 = 0.
Видео:4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать
Ваш ответ
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать
решение вопроса
Видео:Найти уравнение плоскости проходящей через прямую и перпендикулярно плоскостиСкачать
Похожие вопросы
- Все категории
- экономические 43,410
- гуманитарные 33,633
- юридические 17,906
- школьный раздел 608,042
- разное 16,856
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
🔥 Видео
Задача 8. Написать уравнение плоскости, проходящей через точку перпендикулярно вектору.Скачать
2. Уравнение плоскости примеры решения задач #1Скачать
Линия пересечения плоскостейСкачать
Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать
Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать
Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать
Написать канонические и параметрические уравнения прямой в пространствеСкачать
Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать
Уравнение плоскости через 3 точкиСкачать
Составьте уравнение плоскости, проходящей через ось Оу и точку M (3;2;4).Скачать
Уравнение плоскости через 2 точки параллельно векторуСкачать
Найти точку пересечения прямой и плоскостиСкачать
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
