Напишите уравнение плоскости которая проходит через точку e и перпендикулярна вектору ef

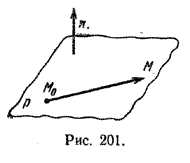
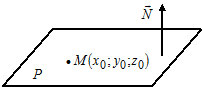Пусть дана некоторая точка M₀ и ненулевой вектор n. Через точку M₀ можно провести только одну плоскость р перпендикулярную вектору n (рис. 201).

Выведем уравнение плоскости р. Пусть М — произвольная точка пространства. Очевидно, что точка М принадлежит плоскости р тогда и только тогда, когда вектор (overrightarrow<M_M>) перпендикулярен вектору n. Как известно, необходимым и достаточным условием перпендикулярности двух векторов является равенство нулю их скалярного произведения. Поэтому уравнение плоскости, проходящей через точку M₀ перпендикулярно вектору n, может быть записано в виде

Вектор n в уравнении (1) называется нормальным вектором плоскости. В качестве нормального вектора можно взять любой вектор, перпендикулярный плоскости.

Пусть точка M₀ и вектор n заданы своими координатами в некоторой прямоугольной системе координат:

Обозначим координаты произвольной точки М плоскости р через х, у и z. Тогда вектор (overrightarrow<M_M>) имеет координаты х — х₀, у — у₀ и z — z₀, а уравнение (1) в координатах записывается следующим образом:

Это уравнение называется уравнением плоскости, проходящей через точку (х₀; у₀; z₀) перпендикулярно вектору (А; В; С).

Задача 1. Найти уравнение плоскости, проходящей через точку М₀(-3; 4; 7) перпендикулярно вектору n = (1; —2; 6).

В данном случае х₀ = -3, у₀ = 4, z₀ = 7; А = 1, В = -2, С = 6. Подставив эти значения в уравнение (2), получим искомое уравнение

3адачa 2. Даны точки M₁ (2; -1; 3) и M₂(4; 5; 0). Написать уравнение плоскости, проходящей через точку М₂ перпендикулярно вектору (overrightarrow<M_M_2>).

За нормальный вектор плоскости можно взять вектор n = (overrightarrow<M_M_2>) = (2; 6; -3). После подстановки координат нормального вектора и координат точки М₀ = М₂(4; 5; 0) в уравнение (2) получим

Задача 3. В треугольнике с вершинами в точках А₁<-5; 2; 7), А₂(5; 0; 6), А₃(0; -1; 2) проведена медиана А₁М₀. Найти уравнение плоскости, проходящей через точку М₀ перпендикулярно медиане А₁М₀.

За нормальный вектор плоскости можно принять вектор n = (overrightarrow<A_M_0>). Определим его координаты. Точка М₀ — середина отрезка А₂А₃, поэтому, если (х₀; у₀; z₀) — ее координаты, то

Координаты нормального вектора n = (А; В; С), следовательно, равны

A = 5 /₂ + 5 = 15 /₂, В = — 1 /₂ — 2 = — 5 /₂, С = 4 — 7 = — 3.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Математический портал

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Nav view search

Navigation

Search

• Вы здесь:
• Home
• Аналитическая геометрия
• Плоскость в пространстве, всевозможные уравнения, расстояние от точки до плоскости.

Видео:10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Плоскость в пространстве, всевозможные уравнения, расстояние от точки до плоскости.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Существуют такие формы записи уравнения плоскости:

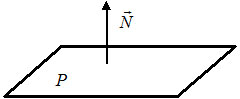
1) $Ax+By+Cz+D=0 -$ общее уравнение плоскости $P,$ где $overline=(A, B, C) -$ нормальный вектор плоскости $P.$

2) $A(x-x_0)+B(y-y_0)+C(z-z_0)=0 -$ уравнение плоскости $P,$ которая проходит через точку $M(x_0, y_0, z_0)$ перпендикулярно вектору $overline=(A, B, C).$ Вектор $overline N$ называется нормальным вектором плоскости.

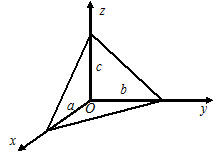
4) $beginx-x_1&y-y_1&z-z_1\x_2-x_1&y_2-y_1&z_2-z_1\x_3-x_1&x_2-x_1&x_3-x_1end=0 — $ уравнение плоскости, которая проходит через три точки $A(x_1, y_1, z_1), B(x_2, y_2, z_2)$ и $C(x_3, y_3, z_3).$

5) $xcosalpha+ycosbeta+zcosgamma-p=0 -$ нормальное уравнение плоскости, где $cosalpha, cosbeta$ и $cosgamma -$ направляющие косинусы нормального вектора $overline,$ направленного из начала координат в сторону плоскости, а $p>0 -$ расстояние от начала координат до плоскости.

Общее уравнение плоскости приводится к нормальному, путем умножения на нормирующий множитель $mu=-frac<sqrt>.$

Расстояние от точки $M(x_0, y_0, z_0)$ до плоскости $P: Ax+By+Cz+D=0$ вычисляется по формуле $$d=left|frac<sqrt>right|.$$

Примеры:

2.180.

а) Заданы плоскость $P: -2x+y-z+1=0$ и точка $M(1, 1, 1).$ Написать уравнение плоскости $P’,$ проходящей через точку $M$ параллельно плоскости $P$ и вычислить расстояние $rho(P, P’).$

Решение.

Так как п.лоскости $P$ и $P’$ параллельны, то нормальный вектор для плоскости $P$ будет также нормальным вектором для плоскости $P’.$ Из уравнения плоскости получаем $overline=(-2, 1, -1).$

Далее запишем уравнение плоскости по формуле ( 2): $A(x-x_0)+B(y-y_0)+C(z-z_0)=0 -$ уравнение плоскости, которая проходит через точку $M(x_0, y_0, z_0)$ перпендикулярно вектору $overline=(A, B, C).$

Ответ: $-2x+y-z+2=0.$

2.181.

а) Написать уравнение плоскости $P’,$ проходящей через заданные точки $M_1(1, 2, 0)$ и $M_2(2, 1, 1)$ перпендикулярно заданной плоскости $P: -x+y-1=0.$

Решение.

Из уравнения плоскости $P,$ находим ее нормальный вектор $overline=(-1, 1, 0).$ Плоскость, перпендикулярная плоскости $P,$ параллельна ее нормальному вектору. Отсюда следует, что можно выбрать точку $M_3(x, y, z)in P’$ такую, что что $overline||overline.$

Поскольку $z_N=0,$ то есть вектор $Nin XoY,$ то $z_=0.$

Мы нашли точку $M_3=(2, 1, 0).$

Так как точка $M_1in P’,$ то и $M_3in P’.$ Запишем уравнение плоскости, которая проходит через три точки $M_1 (1, 2, 0), M_2(2, 1, 1)$ и $M_3(2, 1, 0).$

$(x-1)(-1)0+(-1)z+(y-2)-(-1)z-(-1)(x-1)-(y-2)0=0Rightarrow$ $Rightarrow-z+y-2+z+x-1=0Rightarrow x+y-3=0.$

2.182.

а) Написать уравнение плоскости $P,$ проходящей через точку $M(1, 1, 1)$ параллельно векторам $a_1(0, 1, 2)$ и $a_2(-1, 0, 1).$

Решение.

Поскольку вектор $[a_1, a_2]$ перпендикулярен плоскости векторов $a_1$ и $a_2$ (см. векторное произведение), то он будет также перпендикулярен искомой плоскости. То есть вектор $[a_1, a_2]$ является нормальным для плоскости $P.$ Найдем этот вектор:

Таким образом $overline=[a_1, a_2]=(1, -2, 1).$

Теперь можно найти уравнение плоскости $P,$ по формуле (2), как плоскости, проходящей через точку $M(1, 1, 1)$ перпендикулярно вектору $overline N=(1, -2, 1):$

Ответ: $x-2y+z=0.$

2.183.

а) Написать уравнение плоскости $P,$ проходящей через точки $M_1(1, 2, 0)$ и $M_2(2, 1, 1)$ параллельно вектору $a=(3, 0, 1).$

Решение.

Поскольку вектор $a$ параллелен плоскости $P,$ то для всякого вектора $overline,$ параллельного вектору $a,$ точка $M_3in P.$

Пусть $M_3=(x, y, z).$ Тогда $overline=(x-1, y-2, z).$ Так как $overline||a,$ то $frac<x_>=frac<y_>=frac<z_>.$ $y_a=0,$ то есть вектор $ain XoZ$ и всякий параллельный ему вектор так же будет принадлежать этой плоскости. Таким образом, $y_=y-2=0Rightarrow y=2.$

Из условия параллельности векторов имеем $frac=frac.$ Пусть $x=4,$ тогда $z=1.$

Мы получили точку $M_3=(4, 2, 1).$

Запишем уравнение плоскости, которая проходит через три точки $M_1 (1, 2, 0), M_2(2, 1, 1)$ и $M_3(4, 2, 1).$

$(x-1)(-1)1+1cdot zcdot 0+(y-2)3-3(-1)z-0cdot 1cdot(x-1)-1(y-2)1=0Rightarrow$

$Rightarrow -x+1+3y-6+3z-y+2=0Rightarrow -x+2y+3z-3=0.$

2.184.

а) Написать уравнение плоскости, проходящей через три заданные точки $M_1(1, 2,0),$ $M_2(2, 1, 1)$ и $M_3(3, 0, 1).$

Решение.

Воспользуемся формулой (4):

$Rightarrow -x+1+-2z+2y-4+2z+2x-2-y+2=0Rightarrow x+y-3=0.$

Видео:2. Уравнение плоскости примеры решения задач #1Скачать

Уравнение плоскости, проходящей через заданную точку перпендикулярно к заданной прямой

Данная статья дает представление о том, как составить уравнение плоскости, проходящей через заданную точку трехмерного пространства перпендикулярно к заданной прямой. Разберем приведенный алгоритм на примере решения типовых задач.

Видео:4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

Нахождение уравнения плоскости, проходящей через заданную точку пространства перпендикулярно к заданной прямой

Пусть задано трехмерное пространство и прямоугольная система координат O x y z в нем. Заданы также точка М 1 ( x 1 , y 1 , z 1 ) , прямая a и плоскость α , проходящая через точку М 1 перпендикулярно прямой a . Необходимо записать уравнение плоскости α .

Прежде чем приступить к решению этой задачи, вспомним теорему геометрии из программы 10 — 11 классов, которая гласит:

Через заданную точку трехмерного пространства проходит единственная плоскость, перпендикулярная к заданной прямой.

Теперь рассмотрим, как же найти уравнение этой единственной плоскости, проходящей через исходную точку и перпендикулярной данной прямой.

Возможно записать общее уравнение плоскости, если известны координаты точки, принадлежащей этой плоскости, а также координаты нормального вектора плоскости.

Условием задачи нам заданы координаты x 1 , y 1 , z 1 точки М 1 , через которую проходит плоскость α . Если мы определим координаты нормального вектора плоскости α , то получим возможность записать искомое уравнение.

Нормальным вектором плоскости α , так как он ненулевой и лежит на прямой a , перпендикулярной плоскости α , будет являться любой направляющий вектор прямой a . Так, задача нахождения координат нормального вектора плоскости α преобразовывается в задачу определения координат направляющего вектора прямой a .

Определение координат направляющего вектора прямой a может осуществляться разными методами: зависит от варианта задания прямой a в исходных условиях. К примеру, если прямая a в условии задачи задана каноническими уравнениями вида

x — x 1 a x = y — y 1 a y = z — z 1 a z

или параметрическими уравнениями вида:

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ

то направляющий вектор прямой будет иметь координаты а x , а y и а z . В случае, когда прямая a представлена двумя точками М 2 ( x 2 , y 2 , z 2 ) и М 3 ( x 3 , y 3 , z 3 ) , то координаты направляющего вектора буду определяться как (x3 – x2, y3 – y2, z3 – z2).

Алгоритм для нахождения уравнения плоскости, проходящей через заданную точку перпендикулярно заданной прямой:

— определяем координаты направляющего вектора прямой a : a → = ( а x , а y , а z ) ;

— определяем координаты нормального вектора плоскости α как координаты направляющего вектора прямой a :

n → = ( A , B , C ) , где A = a x , B = a y , C = a z ;

— записываем уравнение плоскости, проходящей через точку М 1 ( x 1 , y 1 , z 1 ) и имеющей нормальный вектор n → = ( A , B , C ) в виде A ( x – x 1 ) + B ( y – y 1 ) + C ( z – z 1 ) = 0 . Это и будет являться требуемым уравнением плоскости, которая проходит через заданную точку пространства и перпендикулярна к данной прямой.

Полученное общее уравнение плоскости: A ( x – x 1 ) + B ( y – y 1 ) + C ( z – z 1 ) = 0 дает возможность получить уравнение плоскости в отрезках или нормальное уравнение плоскости.

Решим несколько примеров, используя полученный выше алгоритм.

Задана точка М 1 ( 3 , — 4 , 5 ) , через которую проходит плоскость, и эта плоскость перпендикулярна координатной прямой О z .

Решение

направляющим вектором координатной прямой O z будет координатный вектор k ⇀ = ( 0 , 0 , 1 ) . Следовательно, нормальный вектор плоскости имеет координаты ( 0 , 0 , 1 ) . Запишем уравнение плоскости, проходящей через заданную точку М 1 ( 3 , — 4 , 5 ) , нормальный вектор которой имеет координаты ( 0 , 0 , 1 ) :

A ( x — x 1 ) + B ( y — y 1 ) + C ( z — z 1 ) = 0 ⇔ ⇔ 0 · ( x — 3 ) + 0 · ( y — ( — 4 ) ) + 1 · ( z — 5 ) = 0 ⇔ z — 5 = 0

Ответ: z – 5 = 0 .

Рассмотрим еще один способ решить данную задачу:

Плоскость, которая перпендикулярна прямой O z будет задана неполным общим уравнением плоскости вида С z + D = 0 , C ≠ 0 . Определим значения C и D : такие, при которых плоскость проходит через заданную точку. Подставим координаты этой точки в уравнение С z + D = 0 , получим: С · 5 + D = 0 . Т.е. числа, C и D связаны соотношением — D C = 5 . Приняв С = 1 , получим D = — 5 .

Подставим эти значения в уравнение С z + D = 0 и получим требуемое уравнение плоскости, перпендикулярной к прямой O z и проходящей через точку М 1 ( 3 , — 4 , 5 ) .

Оно будет иметь вид: z – 5 = 0 .

Ответ: z – 5 = 0 .

Составьте уравнение плоскости, проходящей через начало координат и перпендикулярной к прямой x — 3 = y + 1 — 7 = z + 5 2

Решение

Опираясь на условия задачи, можно утверждать, что за нормальный вектор n → заданной плоскости можно принять направляющий вектор заданной прямой. Таким, образом: n → = ( — 3 , — 7 , 2 ) . Запишем уравнение плоскости, проходящей через точку О ( 0 , 0 , 0 ) и имеющей нормальный вектор n → = ( — 3 , — 7 , 2 ) :

— 3 · ( x — 0 ) — 7 · ( y — 0 ) + 2 · ( z — 0 ) = 0 ⇔ — 3 x — 7 y + 2 z = 0

Мы получили требуемое уравнение плоскости, проходящей через начало координат перпендикулярно к заданной прямой.

Ответ: — 3 x — 7 y + 2 z = 0

Задана прямоугольная система координат O x y z в трехмерном пространстве, в ней – две точки А ( 2 , — 1 , — 2 ) и B ( 3 , — 2 , 4 ) . Плоскость α проходит через точку A перпендикулярно прямой А В . Необходимо составить уравнение плоскости α в отрезках.

Решение

Плоскость α перпендикулярна к прямой А В , тогда вектор А В → будет нормальным вектором плоскости α . Координаты этого вектора определяются как разности соответствующих координат точек В ( 3 , — 2 , 4 ) и А ( 2 , — 1 , — 2 ) :

A B → = ( 3 — 2 , — 2 — ( — 1 ) , 4 — ( — 2 ) ) ⇔ A B → = ( 1 , — 1 , 6 )

Общее уравнение плоскости будет записано в следующем виде:

1 · x — 2 — 1 · y — ( — 1 + 6 · ( z — ( — 2 ) ) = 0 ⇔ x — y + 6 z + 9 = 0

Теперь составим искомое уравнение плоскости в отрезках:

x — y + 6 z + 9 = 0 ⇔ x — y + 6 z = — 9 ⇔ x — 9 + y 9 + z — 3 2 = 1

Ответ: x — 9 + y 9 + z — 3 2 = 1

Также нужно отметить, что встречаются задачи, требование которых – написать уравнение плоскости, проходящей через заданную точку и перпендикулярной к двум заданным плоскостям. В общем, решение этой задачи в том, чтобы составить уравнение плоскости, проходящей через заданную точку перпендикулярно к заданной прямой, т.к. две пересекающиеся плоскости задают прямую линию.

Задана прямоугольная система координат O x y z , в ней – точка М 1 ( 2 , 0 , — 5 ) . Заданы также уравнения двух плоскостей 3 x + 2 y + 1 = 0 и x + 2 z – 1 = 0 , которые пересекаются по прямой a . Необходимо составить уравнение плоскости, проходящей через точку М 1 перпендикулярно к прямой a .

Решение

Определим координаты направляющего вектора прямой a . Он перпендикулярен как нормальному вектору n 1 → ( 3 , 2 , 0 ) плоскости n → ( 1 , 0 , 2 ) , так и нормальному вектору 3 x + 2 y + 1 = 0 плоскости x + 2 z — 1 = 0 .

Тогда направляющим вектором α → прямой a возьмем векторное произведение векторов n 1 → и n 2 → :

a → = n 1 → × n 2 → = i → j → k → 3 2 0 1 0 2 = 4 · i → — 6 · j → — 2 · k → ⇒ a → = ( 4 , — 6 , — 2 )

Таким образом, вектор n → = ( 4 , — 6 , — 2 ) будет нормальным вектором плоскости, перпендикулярной к прямой a . Запишем искомое уравнение плоскости:

4 · ( x — 2 ) — 6 · ( y — 0 ) — 2 · ( z — ( — 5 ) ) = 0 ⇔ 4 x — 6 y — 2 z — 18 = 0 ⇔ ⇔ 2 x — 3 y — z — 9 = 0

Ответ: 2 x — 3 y — z — 9 = 0

📹 Видео

Уравнение плоскости через точку и нормальСкачать

Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Задача 8. Написать уравнение плоскости, проходящей через точку перпендикулярно вектору.Скачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать

Уравнение плоскости через 2 точки параллельно векторуСкачать

Уравнение плоскости через 3 точкиСкачать

Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Видеоурок "Уравнение плоскости по трем точкам"Скачать

Уравнение плоскости. Практическая часть. 11 класс.Скачать

Найти уравнение плоскости проходящей через прямую и перпендикулярно плоскостиСкачать

Составьте уравнение плоскости, проходящей через ось Оу и точку M (3;2;4).Скачать

11 класс, 8 урок, Уравнение плоскостиСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать