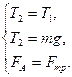Напишите уравнение описывающее движение шарика в жидкости в нестационарном и стационарном режиме (5 видео)

Рассмотрим падение шарика в вязкой жидкости

При движении шарика слой жидкости, граничащий с его поверхностью, прилипает к шарику и движется со скоростью шарика. При вычислении сопротивления среды следует учитывать трение отдельных слоев жидкости друг о друга, а не трение шарика о жидкость.

На шарик, падающий в вязкой жидкости, действуют три силы (рис. 2.2):

· сила тяжести F₁= mg = p_ш×V×g;

· сила Архимеда F_А = p_ж×V×g (равная весу жидкости в объеме шарика);

· сила сопротивления, обусловленная вязкостью жидкости:

F = 6p×h×r×v,

где r_ш – плотность материала шарика;

r_ж – плотность жидкости;

V – объем шарика;

g – ускорение свободного падения.

Все три силы направлены по вертикали: F₁ – вниз, F₂ и F₃ – вверх.

В общем случае уравнение движения шарика имеет вид

Сила сопротивления с увеличением скорости движения шарика возрастает, а ускорение dv/dt уменьшается до тех пор, пока шарик не достигнет такой скорости, при которой ускорение равно 0.

Тогда уравнение (2.3) примет вид:

в этом случае шарик движется с постоянной скоростью v₀.

Решая (2.4) относительно h, получим

(2.5)

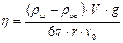
Если теперь учесть, что V = r 3 , r = d/2, v₀ = l/t,

где d – диаметр шарика;

l – длина участка равномерного движения, пройденного за время t,

то формула (2.5) примет окончательный вид

(2.6)

Таким образом, для нахождения h нужно измерить d, l и t.

Рассмотрим подъем шарика в вязкой жидкости.

Если два одинаковых шарика связаны невесомой нитью, перекинутой через блок, причем один из шариков будет погружен в сосуд с жидкостью (2.3.), то уравнения движения шарика имеют вид:

(2.7)

В уравнениях (2.7)

I – момент инерции диска;

R – радиус диска;

Т₁ и Т₂ – натяжение нитей,

F_тр – сила трения, обусловленная вязкостью жидкости,

F_А – сила Архимеда.

Сила сопротивления с увеличением скорости движения шарика возрастает, а ускорение уменьшается до тех пор, пока шарик не достигнет такой скорости v₀, при которой ускорение равно 0.

Тогда уравнения (2.7), при , принимают вид:

В этом случае шарик двигается с постоянной скоростью. Из (2.8) следует

(2.9)

или аналогично формуле (2.6) расчетная формула принимает вид:

(2.10)

В формуле (2.10) так же как и в формуле (2.6) нужно измерить d, l, t.

Описание установки.

Длинный стеклянный цилиндр, наполненный исследуемой жидкостью, имеет две горизонтальные метки А и В, расположенные на расстоянии l друг от друга. Метка А установлена так, что при прохождении через нее шарик уже имеет постоянную скорость v₀ (см. рис 2.2).

При измерении вязкости при подъеме шарика применяется схема (рис. 2.3): на краю стеклянного цилиндра установлен блок, через который перекинуты шарики, связанные нитью. Для определения вязкости при подъеме шарика, один шарик опускают на дно цилиндра с жидкостью.

Видео:Урок 137. Движение тела в жидкости и газе.Скачать

Движение шарика в вязкой среде

Когда тело из твердого материала движется в жидкости, жидкость вынуждена обтекать его. Слой жидкости, прилегающий к поверхности тела, обычно движется вместе с ним, а жидкость на большом удалении от тела покоится. Поэтому в окружении тела существует градиент скорости, в котором диссипирует энергия движения. Это значит, что на движущееся тело действует сила гидродинамического сопротивления. При малых скоростях течения она пропорциональна скорости движения с коэффициентом пропорциональности /, который зависит от размера и формы тела и от вязкости среды. В гидродинамике доказывается, что для сферического тела радиусом г, движущегося поступательно (без вращения) с небольшой скоростью, коэффициент трения /равен бщг, т.е. сила вязкого сопротивления при медленном движении шарика в текучей среде составляет

Это уравнение называют формулой Стокса (G.G. Stokes, 1851).

Когда шарик падает под действием силы тяжести в жидкости, на него действуют силы: 1) собственно сила тяжести /(тяж) = mg 2) выталкивающая сила, равная весу жидкости, которую шарик вытесняет своим объемом /(выт); 3) сила вязкого сопротивления (10.21). Если направление вниз по вертикали считать положительным, то выражение для равнодействующей силы имеет вид F= /(тяж) — /(выт) — /(сопр). Выталкивающая сила равна произведению массы жидкости т₀, которую шарик вытесняет своим объемом, и ускорения свободного падения: /’(выт) = т$, где g — ускорение свободного падения. Таким образом, F = mg — т$ — fv. Разность т-т₀ называют эффективной массой и обозначают т_эфф. То есть эффективная масса — это масса тела, исправленная на массу среды, которую тело вытесняет своим объемом. Таким образом, баланс сил имеет вид:

Если в начальный момент времени шарик покоится, а затем падает, то скорость, конечно, увеличивается под действием силы тяжести. В результате увеличивается сила сопротивления жидкости, но сила тяжести m_effg остается постоянной. Поэтому может быть достигнута скорость, при которой равнодействующая сила в (10.22) равна нулю. Тогда шарик продолжит падение с постоянной скоростью v_s. Ее называют скоростью стационарного или установившегося движения:

Из этого следует выражение для стационарной скорости падения:

Эффективная масса шарика выражается через его объем V= 4%j/3, плотность р материала шарика и р₀ среды, в которой он падает:

Тогда из уравнений (10.24), (10.25), (10.21) следует формула

Она верна при условии, что стационарная скорость не настолько велика, чтобы вызвать завихрения в жидкости при обтекании шарика, и что шарик не вращается при движении. При выполнении этих условий можно вычислить вязкость, если известно время /, за которое шарик проходит известный путь L в стационарном режиме:

В действительности для измерения вязкости жидкостей обычно применяется не свободное падение шарика, а его скатывание по внутренней цилиндрической стенке сосуда, в котором находится жидкость. Такой прибор называют вискозиметром Хепплера. В нем скорость скатывания зависит от трения качения по стенке и от угла наклона вискозиметра. Для определения вязкости время скатывания шарика в приборе калибруют с помощью жидкостей с известными величинами вязкости. Затем вязкость испытуемой жидкости вычисляют из времени скатывания и коэффициента, найденного предварительной калибровкой прибора.

Видео:Движение тел в жидкостях и газах. Лобовое сопротивление и подъемная сила. Формула Стокса. 10 класс.Скачать

Лабораторные работы по электротехнике

ОПРЕДЕЛЕНИЕ ВЯЗКОСТИ ЖИДКОСТИ

Приборы и принадлежности: сосуд с известной жидкостью, микрометр, секундомер, стальные шарики.

Цель работы: определить динамическую и кинематическую вязкости жидкости методом Стокса.

Если происходит движение одного слоя реальной жидкости относительно другого, то при различной относительной скорости движения этих слоев возникают силы внутреннего трения, которые зависят от степени вязкости жидкости. Внутреннее трение подчиняется закону Ньютона:

где f — сила внутреннего трения, действующая на единицу площади поверхностности слоя; h — динамическая вязкость; — градиент скорости по направлению внешней нормали п к поверхности слоя. Знак минус указывает, что сила трения направлена против скорости. Динамическая вязкость (коэффициент внутреннего трения) h равна численно силе внутреннего трения, действующей на единицу площади поверхности слоя при градиенте скорости, равном единице.

Силы сопротивления движению возникают и при падении тела внутри покоящейся жидкости. При этом вокруг движущегося тела возникает мономолекулярный слой жидкости, молекулы которого как бы прилипают к телу за счет сил сцепления и увлекаются этим телом, т.е. имеют скорость движения, равную скорости этого тела.

Этот мономолекулярный слой жидкости, движущейся со скоростью данного тела, увлекает за собой соседние слои жидкости, но с меньшими скоростями, причем чем дальше от тела отстоит слой жидкости, тем с меньшей скоростью он движется по сравнению со скоростью тела.

Силы внутреннего трения действуют со стороны удаленных частиц на прилегающие к телу частицы жидкости, тормозят их и, являясь силами сопротивления, направлены в сторону противоположную скорости тела.

Опытным путем было установлено, что сила сопротивления среды зависит от скорости движения тела, его линейных размеров, состояния поверхности тела и вязкости среды.

Силу сопротивления среды Fс можно наиболее просто определить для тела сферической формы, падающего в покоящейся жидкости. По Стоксу, сила сопротивления среды

где h – динамическая вязкость жидкости; d — диаметр шарика; u — скорость шарика.

Формула Стокса (13.1) положена в основу метода определения вязкости жидкости.

Рассмотрим динамику движения шарика в жидкости (рис.13.1). На шарик, движущийся в жидкости, кроме силы сопротивления Fс действуют еще две силы: сила тяжести Fт= mg= r шVg и выталкивающая сила (сила Архимеда): где r ш — плотность материала шарика; r ж — плотность жидкости; V — объем шарика; g — ускорение свободного падения.

По второму закону Ньютона (в проекциях на ось x) имеем

где а — ускорение шарика

Сила тяжести и сила Архимеда остаются неизменными в данном опыте, а сила сопротивления Fс увеличивается по мере возрастания скорости шарика. При этом ускорение шарика будет уменьшаться до тех пор, пока не станет равным нулю. Дальнейшее движение шарика происходит равномерно со скоростью v, которую приобретает шарик к Рис. 13.1 этому моменту.

Итак, при равномерном движении шарика a=0, и из (13.2) получаем

Подставив это значение силы сопротивления Fс в формулу Стокса (13.1), получим

Подставляя значение объема шарика V= p d3/6 и решая уравнение (13.3) относительно h , находим вязкость жидкости

Скорость u можно определить, используя уравнение равномерного движения

где s — расстояние, пройденное шариком равномерно; t — время его движения.

Окончательно для динамической вязкости имеем формулу

Следует иметь в виду, что коэффициент вязкости сильно зависит от температуры и с ее ростом уменьшается.

Кроме динамической вязкости часто используется понятие кинематической вязкости

где — плотность жидкости.

Установка для определения вязкости представляет собой стеклянный цилиндр, заполненный испытуемой жидкостью (например, глицерином, вазелиновым маслом) закрепленный в вертикальном положении (рис.13.2).

На цилиндре имеются подвижные кольца А и В, которыми фиксируется путь, пройденный шариком в равномерном движении. Верхнее кольцо А должно быть установлено не менее, чем на 20 см ниже уровня жидкости: на этом пути движения шарика стабилизируется. Кольцо В устанавливают как можно дальше от кольца А. Расстояние между кольцами измеряют и записывают. Время падения шарика измеряют электрическим секундомером, который прилагается к установке.

Следует учесть, что погрешность в определении времени падения шарика определяет погрешность результата измерений вязкости.

Порядок выполнения работы

. ПРЕДОСТЕРЕЖЕНИЕ . В стеклянный цилиндр нельзя кидать посторонние предметы. Доставать шарики со дна цилиндра разрешается только лаборанту.

1.Отберите для опыта пять шариков. Микрометром измерьте диаметр каждого шарика в трех различных направлениях и записывают в таблицу.

2.Установите кольца А и В, как описано выше, измерьте расстояние между ними.

3. Шарик бросьте в жидкость как можно ближе к оси сосуда и, наблюдая за его падением, фиксируйте время падения t шарика между кольцами А и В (реагируйте быстро, так как время падения мало!). Опыт повторите с каждым из пяти шариков. Данные опытов занесите в таблицу 13.1.

4. Запишите плотность шариков (сталь) r ш=7900 кг/м3 и плотность исследуемой жидкости (глицерин) r ж=1260 кг/м3. По результатам каждого опыта по формуле (13.4) вычислите динамическую вязкость жидкости, найдите среднее значение и сравните его с табличными данными.