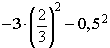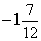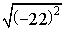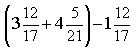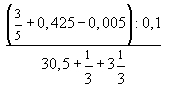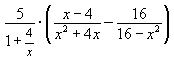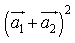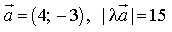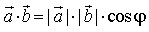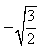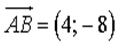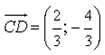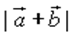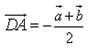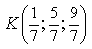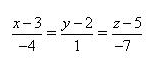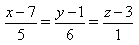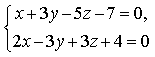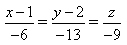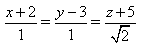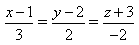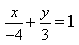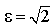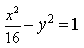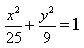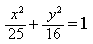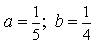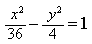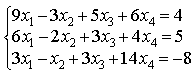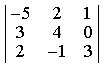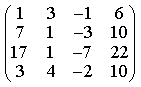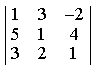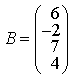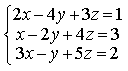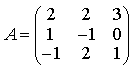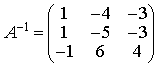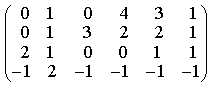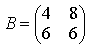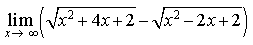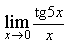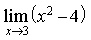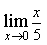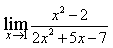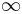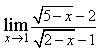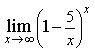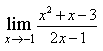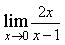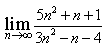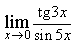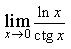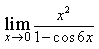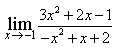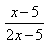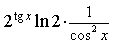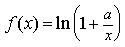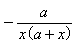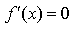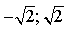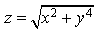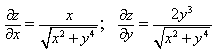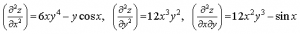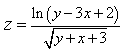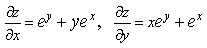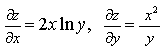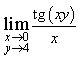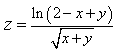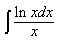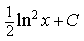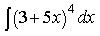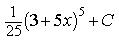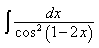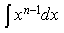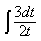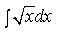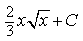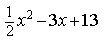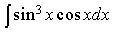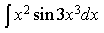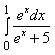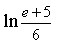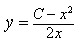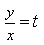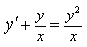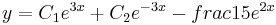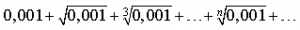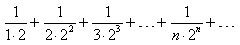Напишите уравнение эллипса если даны его полуоси a 5 и b 4 мти

Ответы на все модули (для контрольного теста) по предмету математика.

Ответы на модуль 1 (ЧИСЛА) по предмету математика.

1) Найдите значение выражения

2) Упростите иррациональное выражение

22

10000

6) Какое из перечисленных чисел является иррациональным?

3,141592…

7) Вычислите

6*5/21

8) Какая из перечисленных дробей является смешанной периодической дробью?

2,75(12)

9) Вычислите с точностью до десятых

0,3

10) Найдите значение выражения 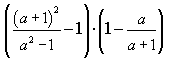при a= 2

2/3

11) Упростите

12) Найдите

-2

13) Какие числа называются целыми?

натуральные числа, числа противоположные натуральным, и число 0

Ответы на модуль 2 (ВЕКТОРНАЯ АЛГЕБРА) по предмету математика.

1) Дано: 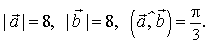Найдите a*b

32

2) Дано: Вычислите

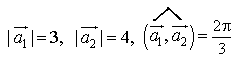
13

3) Найдите l , если

3 или -3

4) Что называется скалярным произведением двух векторов?

число, определяемое по формуле

5) Найдите l , если

2,5 или -2,5

6) Даны векторы 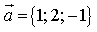и Найдите — проекцию вектора на ось вектора

7) Даны точки M(-5; 7; -6), N(7; -9; 9). Вычислите проекцию вектора 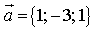на вектор MN

3

8) При каком значении l векторы MP и KD коллинеарны, если M(-3; 2), P(-1; -2), K(2; 1), D(5;l)?

-5

9) Какие векторы называются коллинеарными?

лежащие на одной прямой или параллельных прямых

10) Векторы называются компланарными, если

они лежат в одной плоскости или параллельных плоскостях

11) Какой из перечисленных векторов коллинеарен вектору

12) Векторы a и b взаимно перпендикулярны (ортогональны), причем |a|=5 и |b|=12 . Определите

13

13) Векторы AC=a и BD=d служат диагоналями параллелограмма ABCD. Выразите вектор DA через векторы a и b

Ответы на модуль 3 (АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ) по предмету математика.

1) Найдите координаты точки K пересечения прямой с плоскостью 2x+ 5y- 3z= 0

2) Найдите уравнение прямой, проходящей через точку пересечения прямых 2x + 3y — 8 = 0 и x — 4y + 5 = 0 и через точку M₁(-2; 3)

5x+ 13y— 29 = 0

3) Укажите канонические уравнения прямой, проходящей через точки M₁(3; 2; 5) и M₂(-1; 3; -2)

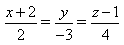
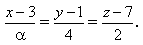
4) Даны прямые и При каком значении a они перпендикулярны?

a= 2

5) Установите взаимное расположение прямых 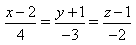и

прямые перпендикулярны

6) Укажите канонические уравнения прямой

7) Найдите острый угол между прямыми 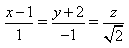и

60°

8) Составьте уравнение плоскости, проходящей через параллельные прямые 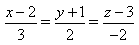и

9) Даны вершины треугольника ABC: A(3; -1),B(4; 2) и C(-2; 0). Напишите уравнения его сторон

10) Уравнение 3x— 4y+ 12 = 0 преобразуйте к уравнению в отрезках

11) Определите уравнение прямой, отсекающей на оси Oy отрезок b = 2 и составляющей с осью Ox угол j= 45°

12) Найдите координаты точки пересечения прямых 2x—y— 3 = 0 и 4x+ 3y— 11 = 0

(2; 1)

13) Найдите уравнение прямой, проходящей через точки M₁(3; 2), M₂(4;-1)

Ответы на модуль 4 (КРИВАЯ 2-ГО ПОРЯДКА) по предмету математика.

1) Определите эксцентриситет равносторонней гиперболы

2) Укажите уравнение окружности, которая проходит через точки А(3;1) и В(-1; 3), а ее центр лежит на прямой 3x—y— 2 = 0

(x— 2) 2 + (y— 4) 2 = 10

3) Укажите уравнение окружности радиуса R= 8 с центром в точке C(2;-5)

(x— 2) 2 + (y+ 5) 2 = 8 2

4) Определите полуоси гиперболы

5) Укажите уравнение окружности, центр которой совпадает с началом координат, а прямая 3x— 4y+ 20 = 0 является касательной к окружности

x 2 +y 2 = 16

6) Укажите уравнение окружности, которая проходит через точку А(2;6) и ее центр совпадает с точкой C(-1; 2)

(x+ 1) 2 + (y— 2) 2 = 25

7) Укажите каноническое уравнение эллипса, расстояние между фокусами которого равно 8, а малая полуось b= 3

8) Напишите уравнение эллипса, если даны его полуоси a= 5 и b= 4

9) Укажите уравнение окружности, проходящей через точку (4; 5) с центром в точке (1; -3)

(x— 1) 2 + (y+ 3) 2 = 73

10) Определите полуоси гиперболы 25x 2 — 16y 2 =1

11) Напишите уравнение гиперболы, фокусы которой лежат на оси Ox, если даны a= 6 и b= 2

12) Укажите уравнение параболы, с вершиной в точке O и фокусом F(4; 0)

13) Укажите уравнение окружности, для которой точки А(3; 2) и В(-1; 6) являются концами одного из диаметров

(x— 1) 2 + (y— 4) 2 = 8

Ответы на модуль 5 (КРИВАЯ 2-ГО ПОРЯДКА) по предмету математика.

1) Найдите общее решение системы

2) Вычислите определитель

-89

3) Найдите ранг и базисные строки матрицы

2. 1-я строка, 2-я строка

4) Вычислите определитель

0

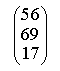
5) Найдите А × В, где ;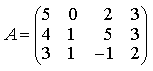

6) Решите систему уравнений методом Крамера

7) Найдите обратную матрицу для матрицы

8) Найдите ранг матрицы

4

9) Определитель системы трех линейных уравнений с тремя неизвестными равен 5. Это означает, что

система имеет единственное решений

11) Метод Гаусса решения системы линейных уравнений предполагает использование

последовательного исключения неизвестных

12) Система линейных уравнений называется совместной, если

она имеет хотя бы одно решение

13) Решите матричное уравнение AX + AXA = B, где ;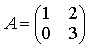

Ответы на модуль 6 (МАТЕМАТИЧЕСКИЙ АНАЛИЗ) по предмету математика.

1) Найдите предел

3

2) Найдите предел

5

3) Найдите предел

5

4) Найдите предел

1/e

5) Найдите предел

0

6) Найдите предел

0

7) Найдите предел

8) Найдите предел

1/2

9) Найдите предел

e — 5

10) Найдите предел

1

11) Найдите предел

0

12) Найдите предел

5/3

13) Найдите предел

3/5

Ответы на модуль 7 (ДИФФЕРЕНЦИРОВАНИЕ) по предмету математика.

1) Вычислите предел по правилу Лопиталя

0

2) Найдите производную функции f(x)=(1+ cos x)sin x

cos x+ cos 2x

3) Вычислите предел по правилу Лопиталя

1/18

4) Вычислите предел по правилу Лопиталя

-4/3

5) Найдите производную функции y= sin(2x 2 + 3)

4xcos(2x 2 + 3)

6) Найдите производную функции y=(3e x +x)× cos x

(3e x + 1) × cos x— (3e x +x) × sin x

7) Для функции 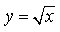найдите y(49)

1/14

8) Найдите производную функции

9) Найдите производную функции y=2 tg x

10) Найдите производную функции

11) Найдите скорость тела, движущего по закону S=3t-5

3

12) Дана функция 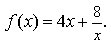Решите уравнение

13) Найдите производную функции y=xe x —e x

xe x

Ответы на модуль 8 (ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНОЙ) по предмету математика.

1) Число f(x₀) называется наибольшим значением функции на отрезке [a;b], если

для всех x из этого отрезка выполняется неравенство f(x) 2 — 3x+ 1

убывает при x 3/2

3) Найдите точки максимума (минимума) функции y=- 5x 2 — 2x+ 2

(-0,2;2,2) — точка максимума

4) Каково необходимое условие возрастания функции?

если функция y=f(x) дифференцируема и возрастает на интервале (a;b), то f(x)>=0 для всех xиз этого интервала

5) Определите поведение функции y= 2x 2 при x= 1

возрастает

6) В каких точках выпукла или вогнута кривая y=x 2 — 3x+ 6

вогнута во всех точках

7) Найдите промежутки возрастания или убывания функции y=- 2x 2 + 8x— 1

(0; 0)

9) Найдите точки перегиба кривой y=x 4 — 12x 3 + 48x 2 — 50

(2; 62) и (4; 206)

10) Найдите точки максимума (минимума) функции y=x 2 — 2x

(1;-1) — точка минимума

11) Вертикальные асимптоты к графику функции 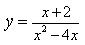имеют вид

12) Найдите наибольшее и наименьшее значения функции y=x 2 на промежутке [-1; 3]

13) В каких точках выпукла или вогнута кривая y= 2 — 3x—x 2

выпукла во всех точках

Ответы на модуль 9 (ФУНКЦИЯ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ) по предмету математика.

1) Найдите частные производные функции двух переменных

2) Найдите частные производные второго порядка функции z=x 3 y 4 +ycos x

3) Найдите предел функции 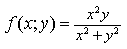при x->0, y->0

0

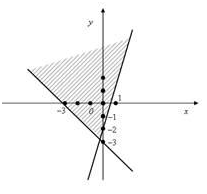
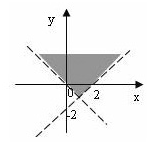
4) На каком из рисунков изображена область определения функции

5) Найдите частные производные функции двух переменных z=xe y +ye x

6) Найдите частные производные функции z=x 2 × ln y

7) Найдите полный дифференциал функции z=x 2 y+xy 2

8) Какая поверхность называется графиком функции n переменных?

9) Укажите полное приращение функции f(x;y)

10) Найдите

4

11) Укажите частное приращение функции f(x;y)по переменной у

12) На каком из рисунков изображена область определения функции

13) Найдите область определения функции

xy 2 не =y 2

Ответы на модуль 10 (НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ) по предмету математика.

1) Найдите

2) Найдите

3) Найдите

4) Найдите

5) Найдите

6) Найдите

7) Найдите

8) Найдите

9) Найдите

10) Найдите 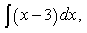если при x= 2 первообразная функция равна 9

11) Найдите

12) Найдите 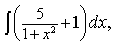если при x=0 первообразная функция равна 0

13) Найдите

Ответы на модуль 11 (ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ) по предмету математика.

1) Скорость точки, движущейся прямолинейно, задана уравнением v=9t 2 -2t-8. Вычислите путь, пройденный точкой за 3 с от начала движения

48 м

2) Вычислите определенный интеграл

9

3) Сила в 6 кГ растягивает пружину на 8 см. Какую работу она производит?

0,24 кГм

4) Вычислите определенный интеграл

5) Вычислите определенный интеграл

e p -1

6) Найдите площадь фигуры, заключенной между прямыми y=4x— 5, x=-3, x=-2 и осью Ox

15

7) Скорость падающего в пустоте тела определяется по формуле v= 9,8t м/сек. Какой путь пройдет тело за первые 10 секунд падения?

490 м

8) Найдите площадь фигуры, ограниченной прямыми y=5x, x=2 и осью Ox

10

9) Вычислите определенный интеграл

2

10) Вычислите определенный интеграл

4*2/3

11) Вычислите определенный интеграл

2/3

12) Вычислите определенный интеграл

0,24

13) Вычислите определенный интеграл

0,25

Ответы на модуль 12 (ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ) по предмету математика.

1) Как называется решение, полученное из общего при конкретных значениях произвольных постоянных?

частным решением

2) Найдите общее решение уравнения (x+y)dx+xdy=0

3) При решении каких уравнений используют подстановку

при решении однородных уравнений

4) Найдите общее решение уравнения xy 2 dy=(x 3 +y 3 )dx

5) Среди перечисленных дифференциальных уравнений укажите уравнение Бернулли

6) Найдите общее решение уравнения y — 9y = e 2 x

7) Найдите общее решение уравнения

8) Найдите частное решение уравнения ds=(4t-3)dt, если при t= 0 s= 0

9) Найдите общее решение уравнения y—y= 0

10) Найдите общее решение уравнения

11) Среди перечисленных дифференциальных уравнений укажите однородное уравнение

12) Найдите общее решение уравнения y— 4y+ 3y= 0

13) Найдите общее решение уравнения y = cos x

Ответы на модуль 13 (РЯДЫ) по предмету математика.

1) Исследуйте сходимость ряда

сходится

2) Найдите интервал сходимости ряда x+2x 2 +3x 3 +4x 4 +…+nx n +…, не исследуя концов интервала

(-1; 1)

3) Найдите радиус сходимости ряда

4) Разложите в степенной ряд f(x)= arctg 3x

5) Исследуйте сходимость ряда

расходится

6) Исследуйте сходимость ряда

сходится

7) Найдите интервал сходимости ряда

8) Исследуйте сходимость ряда

расходится

9) Исследуйте сходимость ряда

расходится

10) Исследуйте сходимость ряда

сходится

11) Разложите в степенной ряд f(x)= sin 2x

12) Исследуйте сходимость ряда

расходится

13) Исследуйте сходимость ряда

сходится

Ответы на задачник по предмету математика.

1) Составьте уравнение плоскости, зная, что точка А(1, -1,3) служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.

x — y + 3z — 11 = 0

2) Вычислить определитель D, разложив его по элементам второго столбца.

-20

3) Вычислить J= ∫cos(lnx) dx/x

sin(lnx)+ C

4) Найти lim _x—>0 (5 x — cos x)

0

5) Вычислить площадь фигуры, ограниченной линиями 4y = x 2 , y 2 = 4x.

16/3

6) Найти производную функции y =ln sinx

ctg x

7) Найдите угол между векторами a = 2m+4n и b = m-n, где m и n — единичные векторы и угол между m и n равен 120 о

120

8) Найти наименьшее значение функции y = x 2 – 6x + 5 на отрезке (1,2).

-3

X1=2, X2=3, X3=-2.

10) При каком положительном значении параметра t прямые, заданные уравнениями
3tx — 8y + 1 = 0 и (1+t)x — 2ty = 0, параллельны?

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Напишите каноническое уравнение эллипса, если даны его полуоси a = 5 и b = 4?

Математика | 10 — 11 классы

Напишите каноническое уравнение эллипса, если даны его полуоси a = 5 и b = 4.

Каноническое уравнение эллипса.

Видео:166. Найти каноническое уравнение эллипса.Скачать

Привести уравнения кривой второго порядка к каноническому виду?

Привести уравнения кривой второго порядка к каноническому виду.

Для эллипса найти координаты вершин и фокусов, для гиперболы — координаты вершин, фокусов и уравнения асимптот, для параболы — координаты фокуса и уравнение директрисы, для окружности — координаты центра и радиус.

Сделать чертеж х * х = (4 — y)(4 + y).

Видео:Написать каноническое уравнение эллипса, если известны b и cСкачать

Напишите каноническое уравнение прямой, проходящей через точку А и перпендикулярной плоскости a под номером 11?

Напишите каноническое уравнение прямой, проходящей через точку А и перпендикулярной плоскости a под номером 11.

Видео:ЭллипсСкачать

Даны А(2, 3, — 2) В(1, — 5, 0) С( — 3, 2, 2) составить каноническое уравнение медианы AP?

Даны А(2, 3, — 2) В(1, — 5, 0) С( — 3, 2, 2) составить каноническое уравнение медианы AP.

Видео:§31.1 Приведение уравнения кривой к каноническому видуСкачать

Напишите каноническое уравнение эллипса, зная что малая ось = 6, а расстояние между директрисами = 13?

Напишите каноническое уравнение эллипса, зная что малая ось = 6, а расстояние между директрисами = 13.

Видео:11 класс, 52 урок, ЭллипсСкачать

Дан эллипс x ^ 2 / 15 + y ^ 2 / 6 = 1?

Дан эллипс x ^ 2 / 15 + y ^ 2 / 6 = 1.

Найти уравнение гиперболы, вершины которой находятся в фокусах, а фокусы — в вершинах данного эллипса.

Видео:Лекция 31.1. Кривые второго порядка. ЭллипсСкачать

Уравнения линии второго порядка привести к каноническому виду, определить тип и построить ее : ?

Уравнения линии второго порядка привести к каноническому виду, определить тип и построить ее : .

Видео:§28 Эксцентриситет эллипсаСкачать

А(4 ; — 6) В(6 ; 4 корень из 6) В задачах 36—40 даны координаты точек А (х1 ; у1) и В (х2 ; y2)?

А(4 ; — 6) В(6 ; 4 корень из 6) В задачах 36—40 даны координаты точек А (х1 ; у1) и В (х2 ; y2).

Требуется : 1) составить каноническое уравнение гиперболы, проходящей через данные точки А и В, если фокусы гиперболы расположены на оси абсцисс ; 2) найти полуоси, фокусы, эксцентриситет и уравнения асимптот этой гиперболы ; 3) найти все точки пересечения гиперболы с окружностью с центром в начале координат, если эта окружность проходит через фокусы гиперболы ; 4) построить гиперболу, ее асимптоты и окружность.

Видео:§18 Каноническое уравнение эллипсаСкачать

Написать уравнение элипса, если даны вершины эллипса A[ — 5 ; 4], B[7 ; 4], а фокус e = 4?

Написать уравнение элипса, если даны вершины эллипса A[ — 5 ; 4], B[7 ; 4], а фокус e = 4.

Видео:165. Найти фокусы и эксцентриситет эллипса.Скачать

Решите уравнение эллипса?

Решите уравнение эллипса.

Если а = 5, эксцентриситет равен 0, 6.

Видео:Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Уравнение эллипса?

Если а = 5, эксцентриситет равен 0, 6.

Вы зашли на страницу вопроса Напишите каноническое уравнение эллипса, если даны его полуоси a = 5 и b = 4?, который относится к категории Математика. По уровню сложности вопрос соответствует учебной программе для учащихся 10 — 11 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

1) 19 / 24 + 5 / 12 — 17 / 36 = 57 / 72 + 30 / 72 — 34 / 72 = 53 / 72 2)11 / 12 + 5 / 9 — 19 / 24 = 66 / 72 + 40 / 72 — 57 / 72 = 49 / 72 3) 13 / 15 — 3 / 10 + 7 / 30 = 26 / 30 — 9 / 30 + 7 / 30 = 24 / 30 = 8 / 10 = 4 / 5.

24 / 8 = 3 3 * 5 = 15 осталось Всего 24 + 15 = 39 листов в тетради.

Группируем 1)9x ^ 2 — 6x + 1 = (3x — 1) ^ 2 2)9y ^ 2 — 12y + 4 = (3y — 2) ^ 2 Получаем (3x — 1) ^ 2 + (3y — 2) ^ 2 = 0 = > 1) и 2) приравниваем к нулю x = 1 / 3 y = 2 / 3 x + y = 1.

4400 * 16 = 70400 70400 — 5814 = 64586 97120 : 16 = 6070 64586 + 6070 = 70656.

1. Строим график у = √х 2. Отображаем симметрично относительно оси Оу. Получаем y = √ ( — x) 3. Смещаем на 3 вправо. Получаем y = √( — x + 3) = √( — (x — 3)).

— 2 * 0, 25 + 5, 19 = — 0, 5 + 5, 19 = 4, 69.

— 2×1 / 4 + 5, 19 = — 1 / 2 + 5, 19 = 4 69 / 100.

15. 1 колпак такого же цвета, что 11. 2 = 12. 3 = 13. И т. д. Иначе не будет выполняться условие для 10 подряд идущих мудрецов. 1 колпак того же цвета, что и второй иначе, не выполниться 2 условие. 2 того же цвета что и 3, и так далее. Получае..

(2 1 / 3 * 1 2 / 7)² * 2 / 9 = 2 1)2 * 1 = * = 3 2) = 9 3) * 9 = 2.

1) AB = AO + OB = 6 + 20 = 26 2) AM = 26 : 2 = 13 3) OM = 13 — 6 = 7 км — ОТВЕТ А. Схема к расчету — в приложении.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Кривые второго порядка. Эллипс: формулы и задачи

Видео:Видеоурок "Гипербола"Скачать

Понятие о кривых второго порядка

Кривыми второго порядка на плоскости называются линии, определяемые уравнениями, в которых переменные координаты x и y содержатся во второй степени. К ним относятся эллипс, гипербола и парабола.

Общий вид уравнения кривой второго порядка следующий:

,

где A, B, C, D, E, F — числа и хотя бы один из коэффициентов A, B, C не равен нулю.

При решении задач с кривыми второго порядка чаще всего рассматриваются канонические уравнения эллипса, гиперболы и параболы. К ним легко перейти от общих уравнений, этому будет посвящён пример 1 задач с эллипсами.

Видео:Эллипс (часть 8). Решение задач. Высшая математика.Скачать

Эллипс, заданный каноническим уравнением

Определение эллипса. Эллипсом называется множество всех точек плоскости, таких, для которых сумма расстояний до точек, называемых фокусами, есть величина постоянная и бОльшая, чем расстояние между фокусами.

Фокусы обозначены как и на рисунке ниже.

Каноническое уравнение эллипса имеет вид:

,

где a и b (a > b) — длины полуосей, т. е. половины длин отрезков, отсекаемых эллипсом на осях координат.

Прямая, проходящая через фокусы эллипса, является его осью симметрии. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка перпендикулярно этому отрезку. Точка О пересечения этих прямых служит центром симметрии эллипса или просто центром эллипса.

Ось абсцисс эллипс пересекает в точках (a, О) и (- a, О), а ось ординат — в точках (b, О) и (- b, О). Эти четыре точки называются вершинами эллипса. Отрезок между вершинами эллипса на оси абсцисс называется его большой осью, а на оси ординат — малой осью. Их отрезки от вершины до центра эллипса называются полуосями.

Если a = b , то уравнение эллипса принимает вид . Это уравнение окружности радиуса a , а окружность — частный случай эллипса. Эллипс можно получить из окружности радиуса a , если сжать её в a/b раз вдоль оси Oy .

Пример 1. Проверить, является ли линия, заданная общим уравнением , эллипсом.

Решение. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:

Ответ. Полученное в результате преобразований уравнение является каноническим уравнением эллипса. Следовательно, данная линия — эллипс.

Пример 2. Составить каноническое уравнение эллипса, если его полуоси соответственно равны 5 и 4.

Решение. Смотрим на формулу канонического уравения эллипса и подставляем: бОльшая полуось — это a = 5 , меньшая полуось — это b = 4 . Получаем каноническое уравнение эллипса:

.

Точки и , обозначенные зелёным на большей оси, где

,

называются фокусами.

называется эксцентриситетом эллипса.

Отношение b/a характеризует «сплюснутость» эллипса. Чем меньше это отношение, тем сильнее эллипс вытянут вдоль большой оси. Однако степень вытянутости эллипса чаще принято выражать через эксцентриситет, формула которого приведена выше. Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.

Пример 3. Составить каноническое уравнение эллипса, если расстояние между фокусами равно 8 и бОльшая ось равна 10.

Решение. Делаем несложные умозаключения:

— если бОльшая ось равна 10, то её половина, т. е. полуось a = 5 ,

— если расстояние между фокусами равно 8, то число c из координат фокусов равно 4.

Подставляем и вычисляем:

Результат — каноническое уравнение эллипса:

.

Пример 4. Составить каноническое уравнение эллипса, если его бОльшая ось равна 26 и эксцентриситет .

Решение. Как следует и из размера большей оси, и из уравнения эксцентриситета, бОльшая полуось эллипса a = 13 . Из уравнения эсцентриситета выражаем число c, нужное для вычисления длины меньшей полуоси:

.

Вычисляем квадрат длины меньшей полуоси:

Составляем каноническое уравнение эллипса:

Пример 5. Определить фокусы эллипса, заданного каноническим уравнением .

Решение. Следует найти число c, определяющее первые координаты фокусов эллипса:

.

Получаем фокусы эллипса:

Видео:Полярные координаты. Полярное уравнение эллипса.Скачать

Решить задачи на эллипс самостоятельно, а затем посмотреть решение

Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:

1) расстояние между фокусами 30, а большая ось 34

2) малая ось 24, а один из фокусов находится в точке (-5; 0)

3) эксцентриситет , а один из фокусов находится в точке (6; 0)

Видео:Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать

Продолжаем решать задачи на эллипс вместе

Если — произвольная точка эллипса (на чертеже обозначена зелёным в верхней правой части эллипса) и — расстояния до этой точки от фокусов , то формулы для расстояний — следующие:

.

Для каждой точки, принадлежащей эллипсу, сумма расстояний от фокусов есть величина постоянная, равная 2a.

Прямые, определяемые уравнениями

,

называются директрисами эллипса (на чертеже — красные линии по краям).

Из двух вышеприведённых уравнений следует, что для любой точки эллипса

,

где и — расстояния этой точки до директрис и .

Пример 7. Дан эллипс . Составить уравнение его директрис.

Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет эллипса, т. е. . Все данные для этого есть. Вычисляем:

.

Получаем уравнение директрис эллипса:

Пример 8. Составить каноническое уравнение эллипса, если его фокусами являются точки , а директрисами являются прямые .

Решение. Смотрим в уравнение директрис, видим, что в нём можем заменить символ эксцентриситета формулой эксцентриситета как отношение первой координаты фокуса к длине большей полуоси. Так сможем вычислить квадрат длины большей полуоси. Получаем:

.

Теперь можем получить и квадрат длины меньшей полуоси:

Уравнение эллипса готово:

Пример 9. Проверить, находится ли точка на эллипсе . Если находится, найти расстояние от этой точки до фокусов эллипса.

Решение. Подставляем координаты точки x и y в уравнение эллипса, на выходе должно либо получиться равенство левой части уравнения единице (точка находится на эллипсе), либо не получиться это равенство (точка не находится на эллипсе). Получаем:

.

Получили единицу, следовательно, точка находится на эллипсе.

Приступаем к нахождению расстояния. Для этого нужно вычислить: число c, определяющее первые координаты фокусов, число e — эксцентриситет и числа «эр» с подстрочными индексами 1 и 2 — искомые расстояния. Получаем:

Проведём проверку: сумма расстояний от любой точки на эллипсе до фокусов должна быть равна 2a.

,

так как из исходного уравнения эллипса .

Одним из самых замечательных свойств эллипса является его оптическое свойство, состоящее в том, что прямые, соединяющие точку эллипса с его фокусами, пересекают касательную к эллипсу под разными углами. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.

📽️ Видео

Эллипс. Определение. Уравнение. График. Фокусы. Главные оси. Эксцентриситет - Новиков АлександрСкачать

Аналитическая геометрия, 7 урок, Линии второго порядкаСкачать

Написать каноническое уравнение гиперболы. Дан эксцентриситетСкачать

§17 Определение эллипсаСкачать