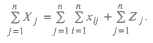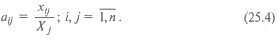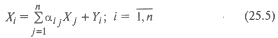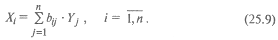Напишите и поясните системы уравнений межотраслевого баланса по строкам и столбцам схемы (5 видео)

Содержание

Межотраслевой баланс
Межотраслевые балансовые модели
Глава 2. Межотраслевые балансовые модели.
2.1. Межотраслевой баланс
2.2. Статическая балансовая модель производства.
Принципиальная схема межотраслевого баланса
🎬 Видео

Видео:Модель межотраслевого баланса. Часть 1 ТеорияСкачать

Межотраслевой баланс

С помощью сервиса в онлайн режиме можно:

найти коэффициенты полных материальных затрат, определить вектор валовой продукции;
составить межотраслевой баланс, составить схему межотраслевого баланса труда;
проверить продуктивность матрицы.

Шаг №1
Шаг №2
Видеоинструкция
Оформление Word

Межотраслевой баланс отражает производство и распределение валового национального продукта в отраслевом разрезе, межотраслевые производственные связи, использование материальных и трудовых ресурсов, создание и распределение национального дохода.

Система уравнений X = AX + Y называется экономико-математической моделью межотраслевого баланса (МОБ) или моделью «затраты — выпуск». C помощью нее можно выполнить следующие расчеты:

подставив в модель объемы валовой продукции каждой отрасли X_i, можно определить объем конечной продукции отрасли Y_j: Y = (E — A)X
задав величины конечной продукции всех отраслей Y_j, можно определить величины валовой продукции каждой отрасли X_i: X = (E — A) -1 Y
установив для ряда отраслей величины валовой продукции, а для всех остальных отраслей задав объемы конечной продукции, можно найти объемы конечной продукции первых отраслей и объемы валовой продукции вторых.

Здесь A – матрица прямых затрат, коэффициенты которой, a_ij показывают затраты i-й отрасли на производство единицы продукции j-й отрасли. Введем обозначение B = (E — A) -1 . Матрица B называется матрицей полных материальных затрат, коэффициенты которой, b_ij показывают полный объем продукции i-й отрасли, используемой для производства единицы продукции j-й отрасли. С учетом линейности соотношений эффект распространения спроса ΔX, вызванный изменением конечного спроса на величину ΔY рассчитывается как: ΔX = B·ΔY
Через C=A-B обозначают матрицу косвенных затрат.

Пример №1 . Для трехотраслевой экономической системы заданы матрица коэффициентов прямых материальных затрат A и вектор конечной продукции Y .

Пример №2 . Дан межотраслевой баланс трехотраслевой модели хозяйства:

№ отрасли потребления	1	2	3	Конечный продукт	Валовый продукт	Y’
№ отрасли	1	20	20	60	100	200	150
отрасли	2	20	40	60	80	200	100
производства	3	20	0	10	70	100	100

Определить:
1) технологическую матрицу;
2) матрицу коэффициентов полных затрат;
3) дать экономический анализ каждого столбца матрицы коэффициентов полных затрат;
4) определить валовый выпуск X’ на новый ассортимент конечной продукции Y’;

Решение.
Находим валовой объем продукции x_i;
x₁ = 20 + 20 + 60 + 100 = 200
x₂ = 20 + 40 + 60 + 80 = 200
x₃ = 20 + 0 + 10 + 70 = 100

Отрасль	Потребление			Конечный продукт	Валовой выпуск
Производство	20	20	60	100	200
	20	40	60	80	200
	20	0	10	70	100

По формуле a_ij = x_ij / x_j находим коэффициенты прямых затрат:
a₁₁ = 20/200 = 0.1; a₁₂ = 20/200 = 0.1; a₁₃ = 60/100 = 0.6; a₂₁ = 20/200 = 0.1; a₂₂ = 40/200 = 0.2; a₂₃ = 60/100 = 0.6; a₃₁ = 20/200 = 0.1; a₃₂ = 0/200 = 0; a₃₃ = 10/100 = 0.1;

0.1	0.1	0.6
0.1	0.2	0.6
0.1	0	0.1

Определим матрицу коэффициентов полных затрат с помощью формул обращения невырожденных матриц.
а) Находим матрицу (E-A):

(E-A) =

0,9	-0,1	-0,6
-0,1	0,8	-0,6
-0,1	0	0,9

б) Вычисляем обратную матрицу (E-A) -1 :

0,9	-0,1	-0,6
-0,1	0,8	-0,6
-0,1	0	0,9

Найдем величины валовой продукции трех отраслей

X’ = (B -1 *Y’) =

1,23	0,15	0,92
0,26	1,28	1,03
0,14	0,0171	1,21

150

100

292

270

144

Пример №3 . В модели межотраслевого баланса

Производство	Потребление			Конечная продукция	Валовая продукция
Производство	1	2	3	Конечная продукция	Валовая продукция
1	10	5	15	70	100
2	20	…	…	…	…
3	30	…	…	…	…
Оплата труда	30	…	…	…	…
Прибыль D	D	…	…	…	…

прибыль D равна:
D = Валовая продукция – Затраты на производство – Оплата труда = 100 – (10+20+30) – 30 = 10.

Видео:Модель Леонтьева. Теория и решение задачи.Скачать

Межотраслевые балансовые модели

Видео:Модель межотраслевого баланса. Часть 2 ПрактикаСкачать

Глава 2. Межотраслевые балансовые модели.

Видео:Модель Леонтьева "затраты-выпуск" в MS ExcelСкачать

2.1. Межотраслевой баланс

Часто при экономическом планировании на уровне регионов или страны в целом возникает необходимость определения объема выпуска товаров, обеспечивающего заданный спрос населения и производственные нужды. Решить эту задачу можно с использованием балансовых моделей производства и распределения продукции. В. основе построения этих моделей лежит балансовый метод, т. е. метод взаимного сопоставления имеющихся материальных, трудовых и финансовых ресурсов с потребностью в них.

Балансовые методы планирования можно рассматривать на различных уровнях иерархии экономических объектов: предприятиях, объединениях, отраслях, народном хозяйстве в целом. Модель межотраслевого баланса (МОБ) исторически является первой экономико-математической моделью сводного народнохозяйственного планирования. Первые балансы народного хозяйства были разработаны Центральным статистическим управлением СССР в гг. В настоящее время межотраслевые балансы на национальном уровне составляются приблизительно в восьмидесяти странах мира. Также строятся межотраслевые балансы на уровне регионов и крупных городов

Предшественниками МОБ были: экономическая таблица Ф. Кенэ (1758) и схемы общественного воспроизводства К. Маркса (XIX в.). Русский экономист (), изучая межотраслевые связи, впервые использовал для этой цели линейные уравнения и предложил технологические коэффициенты. Автором современной модели межотраслевого баланса (в англоязычных странах он имеет название «input-output analysis») является американский ученый (русский по происхождению) Василий Леонтьев. В 1973 году за разработанные методы экономического анализа (модель “затраты–выпуск ”) ему была присуждена Нобелевская премия.

Эта модель позволяет рассчитывать полные затраты валовой продукции, прямые и косвенные затраты на единицу продукции, а также дает возможность устанавливать четкие количественные соотношения между валовым общественным продуктом, национальным доходом, развитием отдельных отраслей экономики Метод универсален. С его помощью американцы, например, проводили перестройку экономики с военных рельсов на мирные. Он был положен в основу индикативных планов, применяемых в Японии.

Межотраслевой баланс производства и распределения продукции – инструмент анализа и планирования структуры общественного производства, учитывающий комплексные взаимосвязи отраслей производственной сферы. В зависимости от того, в каких единицах измеряются потоки продуктов в балансе, существует различные варианты межотраслевых балансов: в натуральном выражении, в стоимостном, в натурально-стоимостном, в трудовых измерителях. По экономическому содержанию информации балансы можно разделить на плановые и отчетные; по характеру используемой модели – на статические и динамические.

Рассмотрим фрагмент (три раздела) отчетного межотраслевого баланса (МОБ), в котором потоки продукции измеряются на основе стоимости произведенной продукции в некоторых фиксированных ценах (табл. 1). Основу баланса составляет совокупность отраслей материального производства. В межотраслевом балансе понятие отрасли отличается от общепринятого, здесь используется понятие “чистой” (или технологической), т. е. условной отрасли, объединяющей все производство данного продукта независимо от ведомственной подчиненности предприятий и фирм.

Фрагмент таблицы межотраслевого баланса

Каждая отрасль дважды фигурирует в балансе: как производящая и как потребляющая. Отрасли как производителю продукции соответствует определенная строка таблицы, а как потребителю продукции – определенный столбец . Так как отрасли являются чистыми, индекс отрасли можно отождествить как с видом товара, так и с технологическим процессом..

В первом разделе содержится информация о межотраслевых связях. Величины находящиеся на пересечении отраслей (т. е. строк и столбцов таблицы) нужно понимать как стоимость средств производства, произведенных в -ой отрасли и потребляемых в качестве материальных затрат в -ой отрасли (межотраслевые поставки продукции, обусловленные производственной деятельностью отраслей). .

Таким образом, каждая -ая строка первого раздела показывает распределение продукции –ой отрасли между другими отраслями народного хозяйства. – производственное потребление продукции -ой отрасли экономической системой (промежуточный продукт. –ой отрасли).

В столбцах первого раздела баланса отражается структура материальных затрат каждой отрасли. – суммарные производственные затраты -ой отрасли в отчетном периоде. – суммарные производственные затраты всех отраслей или суммарный промежуточный продукт народного хозяйства.

Таким образом, первый раздел МБ показывает общую картину производственных затрат и распределения продукции отраслей на производственные цели. Данные I квадранта играют решающую роль в анализе структуры материальных затрат отраслей, пропорций и производственных связей между отраслями, потоков системе материально-технического снабжения.

Во втором разделе содержатся величины – значения конечного продукта и – значения валового продукта ().

Конечный продукт – это продукция отраслей материального производства, поступающая на цели личного и общественного непроизводственного потребления, накопление и возмещение выбытия основных фондов, прирост запасов, затраты на просвещение, здравоохранение, экспорт и т. д.).

– суммарный конечный продукт экономической системы или национальный доход, а столбец характеризует материальную структуру национального дохода.

В развернутых схемах баланса конечный продукт каждой отрасли показывают дифференцировано по направлениям использования: для потребления, инвестиции, прирост запасов и резервов, экспорт и прочие расходы.

Первый и второй раздел межотраслевого баланса называют таблицей «затраты-выпуск». По строкам этой таблицы строится следующее балансовое соотношение:

, (), (2.1),

т. е. валовой продукт каждой отрасли равен сумме конечного и промежуточного продуктов.

В третьем разделе МБ отражается стоимостная структура валового продукта отраслей. В нашей таблице третий раздел представлен 2-я строками. В первой стоят величины , каждая из которых означает добавленную стоимость (условно-чистую продукцию) отрасли, а во второй––валовой продукт. Условно–чистая продукция определяется как разность между валовой продукцией и суммарными производственными затратами:

(2.2)

Добавленная стоимость — это та часть стоимости продукта, которая создается в данной отрасли, Она отражает прибыль, заработную плату, амортизационные отчисления, налоги и прочие издержки, понесенные каждым объектом (отраслью) в дополнение к платежам за ресурсы, поступившие из других отраслей.

Обычно в развернутых МБ условно-чистую продукцию подразделяют на амортизационные отчисления и чистую продукцию.

Из соотношений (2.1) и (2.2) следует

(2.3),

откуда получаем: (2.4)

Это соотношение показывает, что суммарный конечный продукт экономической системы (национальный доход) равен суммарной условно–чистой продукции. Таким образом, третий раздел также характеризует национальный доход, но со стороны его стоимостного состава как сумму оплаты труда и чистого дохода всех отраслей материального производства, а величины показывают вклад отрасли в национальный доход.

Данные третьего раздела необходимы для анализа соотношений между вновь созданной и перенесенной стоимостью, между величиной необходимого и прибавочного продукта в целом по материальному производству и в отраслевом разрезе. В целом же уравнение (2.4) показывает, что в межотраслевом балансе соблюдается важнейший принцип единства материально-вещественного и стоимостного состава национального дохода.

Следует отметить, что баланс в натуральных измерителях обычно содержит только показатели I и II разделов схемы межотраслевого баланса. Он разрабатывается по важнейшим видам продукции и обычно не охватывает всего общественного производства.

Подчеркнем, что рассмотренный нами отчетный МБ – это пока не модель, а лишь способ представления статистической информации об экономике страны. Он строится на основе агрегирования результатов отдельных предприятий. Кроме отчетных МБ разрабатываются плановые МБ. Для их построения необходимо использовать межотраслевые балансовые модели.

Видео:Решение системы уравнений методом обратной матрицы.Скачать

2.2. Статическая балансовая модель производства.

Балансовая модель строится на следующих предположениях о свойствах экономического объекта:

· Экономическая система состоит из нескольких экономических объектов. Количество выпускаемой каждым объектом продукции может быть охарактеризовано одним числом, в качестве которого чаще всего рассматривается валовой выпуск в некоторых фиксированных ценах.

· Выпускаемая каждым объектом продукция частично потребляется другими объектами системы, а частично поступает вовне в качестве конечного продукта данной системы, т. е. выполняется соотношение

(2.5)

· Цель системы заключается в производстве заданного количества конечного продукта.

· Свойство комплектности потребления: для выпуска заданного количества продукта объект должен получать строго определенное количество других продуктов.

· Свойство линейности потребления: увеличение выпуска продукции в некоторое число раз требует увеличения потребления объектом всех других продуктов в то же самое число раз.

Очевидно, что сформулированные предположения лишь приближенно отражают реальную экономическую ситуацию, к примеру, предположение о комплектности потребления, которое предполагает, что технология производства в каждом объекте остается неизменной в течение рассматриваемого промежутка времени, причем в каждой отрасли имеется единственная технология производства, не допускается замещение одного ресурса другим.

В реальном производстве один и тот же продукт в зависимости от применяемой технологии может требовать различное количество инградиентов, а в модели предполагается, что продукт производится некоторым усредненным способом. Несмотря на эти упрощения, балансовая модель является удобным инструментом планирования благодаря своей простоте и возможности расчета всех показателей плана.

Выберем в качестве переменных модели величины валового выпуска — . (). В силу предположения 2 часть этого продукта уходит из системы в качестве конечного продукта . Величины рассматривается в модели как плановое задание, при этом выполняется соотношение (2.5):

()

Свойства линейности и комплектности потребления определяют закономерности преобразования ресурсов в системе, а именно, согласно свойству комплектности для выпуска единицы продукции – ый объект должен использовать другие продукты рассматриваемой экономической системы в определенном соотношении. Пусть `-вектор, определяющий это соотношение, где величины называют технологическими коэффициентами или коэффициентами прямых затрат

– количество продукции — ой отрасли, необходимоe для производства единицы продукции в j-ой отрасли. Величины не зависят от объема производства и являются относительно стабильными величинами во времени.

Матрица, составленная из величин называется матрицей технологических коэффициентов или матрицей прямых затрат

Из экономического смысла величин следует, что все элементы матрицы не отрицательны. Будем это свойство записывать так: . Так как процесс воспроизводства нельзя было бы осуществлять, если бы для собственного производства в отрасли затрачивалось большее количество продукта, чем создавалось, то очевидно, что диагональные элементы матрицы меньше 1:

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Принципиальная схема межотраслевого баланса

Производящие отрасли	Потребляющие отрасли	Конечный продукт	Валовой продукт
1-я	2-я	3-я	.	j-я
1-я 2-я 3-я . . . i-я	x_1-1 х_2-1 х_3-1 . . . х_i₁	x_l_-2 x_2-2 x_3-2 . . . x_i₂	x_l_-3 x_2-3 х_3-3 . . . x_i₃	. . . . I . .	x₁_j х₂_j х₃_j x_ij	у₁ у₂ у_З . II . у_i	x₁ х₂ х₃ . . . х_i
Амортизация Оплата труда Чистый доход	c₁ v₁ m₁	c₂ v₂ m₂	с₃ v₃ m₃	. III .	c_j v_j m_j	IV
Валовой продукт	x₁	x₂	х₃	.	x_j

Рассмотрим схему МОБ в разрезе его крупных составных частей. Выделяются четыре части, имеющие различное экономическое содержание, которые называются квадрантами баланса и на схеме обозначены римскими цифрами.

Первый квадрант МОБ – это прямоугольная таблица межотраслевых материальных связей. Показатели таблицы представляют собой величины прямых межотраслевых потоков продукции и обозначаются как х_ij, где i и j – соответственно номера производящих и потребляющих отраслей. Таким образом, этот квадрант имеет вид квадратной матрицы п, сумма всех элементов которой равна годовому фонду возмещения затрат средств производства в материальной сфере.

Во втором квадранте представлена конечная продукция всех отраслей, выходящая из сферы производства на потребление и накопление. В таблице этот раздел дан укрупненно – в виде одного столбца величин y_i, но в развернутой схеме МОБ конечный продукт каждой отрасли дается дифференцированно по направлениям использования: на личное и общественное потребление, на накопление, экспорт и т.д. Следовательно, второй квадрант характеризует отраслевую материальную структуру национального дохода.

Третий квадрант МОБ также характеризует национальный доход, но со стороны его стоимостного состава, как сумму чистой продукции и амортизации; чистая продукция понимается при этом как сумма оплаты труда и чистого дохода отраслей. Сумму амортизации C_j и чистой продукции (V_j + m_j) j-й отрасли будем называть условно чистой продукцией и обозначать в дальнейшем как Z_j.

Четвертый квадрант, который находится на пересечении столбцов второго квадранта и строк третьего квадранта, отражает конечное формирование и использование национального дохода. Таким образом, общий итог этого квадранта, так же как второго и третьего, должен быть равен созданному за год национальному доходу.

Валовая продукция отраслей не входит в рассмотренные выше четыре квадранта, а представлена в виде столбца справа от второго квадранта и в виде строки ниже третьего квадранта. Строка и столбец валовой продукции замыкают схему МОБ и играют важную роль как для проверки самого баланса, так и для разработки экономико-математической модели МОБ. Если обозначить валовую продукцию некоторой отрасли буквой с индексом, равным номеру данной отрасли, то можно записать два соотношения, отражающих сущность МОБ и являющихся основой его экономико-математической модели.

Во-первых, рассматривая схему баланса по столбцам, можно сделать вывод, что итог материальных затрат любой потребляющей отрасли и ее условно чистой продукции равен валовой продукции этой отрасли:

Соотношения (25.1) задают систему п уравнений, отражающих стоимостной состав продукции всех отраслей материальной сферы.

Во-вторых, если рассматривать схему МОБ по строкам для каждой производящей отрасли, то можно увидеть, что валовая продукция той или иной отрасли равна сумме материальных затрат отраслей, потребляющих ее продукцию, и конечной продукции данной отрасли:

Формула (25.2) описывает систему из и уравнений, которые называются уравнениями распределения продукции отраслей материального производства по направлениям использования.

Просуммируем по всем отраслям уравнения (25.1), в результате получим:

Аналогичное суммирование уравнений (25.2) дает следующий результат:

Левые части обоих равенств равны между собой, так как представляют собой весь валовой общественный продукт. Первые слагаемые правых частей этих равенств также равны между собой, их величина равна итогу первого квадранта. Следовательно, должно соблюдаться соотношение:

Левая часть уравнения (25.3) есть сумма третьего квадранта, а правая – итог второго квадранта. В целом же это уравнение показывает, что в МОБ соблюдается важнейший принцип единства материального и стоимостного состава национального дохода.

Экономико-математическая модель МОБ. Основу информационного обеспечения модели межотраслевого баланса составляет технологическая матрица, содержащая коэффициенты прямых материальных затрат на производство единицы продукции. Эта матрица является также основой экономико-математической модели МОБ. Предполагается, что для производства единицы продукции в j-й отрасли требуется определенное количество затрат промежуточной продукции i-й отрасли, равное а_ij. Оно не зависит от объема производства в j-й отрасли и является довольно стабильной величиной во времени. Величины a_ij называются коэффициентами прямых материальных затрат и рассчитываются так:

Таким образом, имеет место определение: коэффициент прямых материальных затрат а_ij показывает, какое количество продукции i-й отрасли необходимо для производства единицы продукции j-й отрасли (с учетом только прямых затрат).

Используя формулу (25.4), систему уравнений баланса (25.2) можно переписать в следующем виде:

Если ввести в рассмотрение матрицу коэффициентов прямых материальных затрат А = (a_ij), а также вектор-столбец валовой продукции X и вектор-столбец конечной продукции Y:

то система уравнений (25.5) в матричной форме примет такой вид:

Система уравнений (25.5), или она же в матричной форме (25.6), называется экономико-математической моделью межотраслевого баланса (моделью В. Леонтьева, моделью «затраты -выпуск»). С ее помощью можно выполнять три варианта расчетов.

1. Задав в модели величины валовой продукции каждой отрасли (X_i), можно определить объем конечной продукции каждой отрасли (Y_i):

2. Задав величины конечной продукции всех отраслей (Y_i), можно определить величины валовой продукции каждой отрасли (X_i):

3. Задав для ряда отраслей величины валовой продукции, а для всех остальных отраслей объемы конечной продукции, можно найти величины конечной продукции первых отраслей и объемы валовой продукции вторых. В этом варианте расчета удобнее пользоваться не матричной формой модели (25.6), а системой линейных уравнений (25.5).

В формулах (25.7) и (25.8) Е обозначает единичную матрицу n-го порядка, а (Е – A) -1 обозначает матрицу, обратную матрице (Е – А). Если определитель матрицы (Е – А) не равен нулю, т.е. эта матрица невырожденная, то обратная ей матрица существует. Обозначим последнюю так:

Тогда систему уравнений в матричной форме (25.8) можно записать в виде:

Элементы матрицы В будем обозначать через b_ij, тогда из матричного уравнения (25.8′) для любой i-й отрасли можно получить следующее соотношение:

Из соотношений (25.9) следует, что валовая продукция выступает как взвешенная сумма величин конечной продукции, причем весами являются коэффициенты b_ij, которые показывают, сколько всего нужно произвести продукции i-й отрасли для выпуска в сферу конечного использования единицы продукции j-й отрасли. В отличие от коэффициентов прямых затрат а_ij коэффициенты b_ij называются коэффициентами полных материальных затрат и включают в себя как прямые, так и косвенные затраты всех порядков. Если прямые затраты отражают количество средств производства, израсходованных непосредственно при изготовлении данного продукта, то косвенные относятся к предшествующим стадиям производства и входят в производство продукта не прямо, а через другие (промежуточные) средства производства. Более детально этот вопрос рассматривается в следующем разделе.

Дадим определениекоэффициента полных затрат: коэффициент полных материальных затрат b_ij показывает, какое количество продукции i-й отрасли нужно произвести, чтобы с учетом прямых и косвенных затрат этой продукции получить единицу конечной продукции j-й отрасли.

Коэффициентами полных материальных затрат можно пользоваться, когда необходимо определить, как скажется на валовом выпуске некоторой отрасли предполагаемое изменение объемов конечной продукции всех отраслей:

где ∆Х_ij, и ∆Y_j – изменения (приросты) величин валовой и конечной продукции соответственно.

Коэффициенты прямых и полных материальных затрат, связь между ними, методы расчета.Переходя к анализу модели МОБ, необходимо прежде всего рассмотреть основные свойства матрицы коэффициентов прямых материальных затрат А. Коэффициенты прямых затрат по определению являются неотрицательными, следовательно, матрица А в целом может быть названа неотрицательной: А ≥ 0. Так как процесс воспроизводства нельзя осуществлять, если для собственного воспроизводства в отрасли затрачивается большее количество продукта, чем создается, то очевидно, что диагональные элементы матрицы А меньше единицы: а_ii АХ. Это означает существование положительного вектора конечной продукции Y > 0 для модели МОБ (25.6).

Рассматривая вычислительные аспекты решения задач на основе модели МОБ, отметим, что основной объем расчетов связан с вычислением матрицы коэффициентов полных материальных затрат В. Если матрица коэффициентов прямых материальных затрат А задана и является продуктивной, то матрицу В можно находить либо по формулам прямого обращения матриц, либо с использованием итерационных методов. Одним из наиболее употребительных методов обращения матриц является метод Жордана. Часто применяется также метод, основанный на применении формулы:

где в числителе стоит так называемая присоединенная матрица, составленная из алгебраических дополнений для элементов транспонированной матрицы (Е – А)’, а в знаменателе находится определитель матрицы (Е – A). В свою очередь, алгебраическое дополнение для элемента матрицы с индексами i и j получается путем умножения множителя (–1) i + j на минор, получаемый после вычеркивания из матрицы i-й строки и j-го столбца.

Рассмотрим пример. Для трехотраслевой экономической системы заданы матрица коэффициентов прямых материальных затрат и вектор конечной продукции:

Необходимо найти коэффициенты полных материальных затрат и вектор валовой продукции, а также заполнить схему межотраслевого материального баланса.

1. Определим матрицу коэффициентов полных материальных затрат, используя формулу (25.11) и методы матричной алгебры:

2. Найдем величины валовой продукции трех отраслей (вектор X), используя формулу (25.8′):

3. Для определения элементов первого квадранта материального межотраслевого баланса в нашей задаче воспользуемся формулой, вытекающей из формулы (25.4): х_ij = а_ij · Х_j. Из этой формулы следует, что для получения первого столбца первого квадранта нужно элементы первого столбца заданной матрицы А умножить на Х₁ = 775,3, элементы второго столбца А – на Х₂ = 510,1, а третьего столбца – на Х₃= 729,6.

Составляющие третьего квадранта (условно чистая продукция) находятся с учетом формулы (25.1) как разность между объемами валовой продукции и суммами элементов соответствующих столбцов найденного первого квадранта.

Четвертый квадрант в нашей задаче состоит из одного показателя и служит, в частности, для контроля правильности расчета: сумма элементов второго квадранта должна в стоимостном материальном балансе совпадать с суммой элементов третьего квадранта.

Результаты расчета представлены в табл. 25.2.