Как составить уравнение высоты треугольника по координатам его вершин?
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.
Следовательно, для составления уравнения высоты треугольника нужно:
- Найти уравнение стороны треугольника.
- Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.
Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).
Написать уравнения высот треугольника.
1) Составим уравнение стороны BC треугольника ABC.
Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:
Таким образом, уравнение прямой BC —
Угловой коэффициент прямой, перпендикулярной BC,
Значит, уравнение высоты, проведённой к стороне BC, имеет вид
Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:
Итак, уравнение высоты, проведённой к стороне BC:
2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):
Уравнение прямой AB:
Угловой коэффициент перпендикулярной ей прямой
Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):
Угловой коэффициент прямой, перпендикулярной AC,
Таким образом, уравнение перпендикулярной AC прямой имеет вид
Подставив в него координаты точки B(5;-3), найдём b:
Итак, уравнение высоты треугольника ABC, опущенной из вершины B:
Видео:Вычисляем высоту через координаты вершин 1Скачать

Решить треугольник Онлайн по координатам
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
| A ( ; ), B ( ; ), C ( ; ) | Примечание: дробные числа записывайте Округлять до -го знака после запятой. Видео:Уравнения стороны треугольника и медианыСкачать  Уравнение высоты треугольника по координатам формулаКак составить уравнение высоты треугольника по координатам его вершин? Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону. Следовательно, для составления уравнения высоты треугольника нужно:
Дано: ΔABC, A(-7;2), B(5;-3), C(1;8). Написать уравнения высот треугольника. 1) Составим уравнение стороны BC треугольника ABC. Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её: Таким образом, уравнение прямой BC — Угловой коэффициент прямой, перпендикулярной BC, Значит, уравнение высоты, проведённой к стороне BC, имеет вид Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b: Итак, уравнение высоты, проведённой к стороне BC: 2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3): Уравнение прямой AB: Угловой коэффициент перпендикулярной ей прямой Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5. Угловой коэффициент прямой, перпендикулярной AC, Таким образом, уравнение перпендикулярной AC прямой имеет вид Подставив в него координаты точки B(5;-3), найдём b: Итак, уравнение высоты треугольника ABC, опущенной из вершины B: Даны координаты вершин треугольника 1) Вычислить длину стороны 2) Составить уравнение линии 3) Составить уравнение высоты, проведенной из вершины А, и найти ее длину. 4) Найти точку пересечения медиан. 5) Найти косинус внутреннего угла при вершине В. 6) Найти координаты точки М, расположенной симметрично точке А, относительно прямой ВС.
1. Длина стороны ВС равна модулю вектора
2. Уравнение прямой ВС: 3. Уравнение высоты АК запишем как уравнение прямой, проходящей через точку
4. Найдем координаты точки N – середины стороны ВС:
Точка пересечения медиан О делит каждую медиану на отрезки в отношении Используем формулы деления отрезка в данном отношении 5. Косинус угла при вершине В найдем как косинус угла между векторами
6. Точка М, симметричная точке А относительно прямой ВС, расположена на прямой АК, перпендикулярной к прямой ВС, на таком же расстоянии от прямой, как и точка А. Координаты точки К найдем как решения системы Точка К является серединой отрезка АМ. Контрольные варианты к задаче 2 Даны координаты вершин треугольника АВС. Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение линии ВС; 3) составить уравнение высоты, проведенной из вершины А; 4) вычислить длину высоты, проведенной из вершины А; 5) найти точку пересечения медиан; 6) вычислить внутренний угол при вершине В; 7) найти координаты точки М, расположенной симметрично точке А относительно прямой ВС.
Не нашли то, что искали? Воспользуйтесь поиском: Лучшие изречения: Учись учиться, не учась! 10637 –
Вы можете заказать решение работы Нужны сторона AB, высота CD, медиана AE и площадь. Координаты вершин А(-8;-3) В(4;-12) С(8;10) Уравнение прямой, проходящей через две точки (x1,y1) и (x2,y2), описывается уравнением: Для прямой AB: Для отыскания уравнения высоты CD найдем сначала уравнение прямой, которая ей перпендикулярна. Это прямая AB (уравнение у нас есть). Выразим y через x явно: Если прямая задана уравнением y = kx+b, то перпендикулярная ей прямая будет иметь вид y = (-1/k)x + d. Поэтому искомая высота имеет уравнение: y = (4/3)x + d. Постоянную d найдем из условия, что высота проходит через точку С. 10 = (32/3) + d, Таким образом, уравнение высоты CD: y = (4/3)x – 2/3, или, что то же, 4x-3y-2 = 0 Медиана AE проходит через две точки – точку А и середину отрезка BC. Найдем координаты середины BC по формуле: Теперь ищем уравнение прямой, идущей через две точки: A(-8;-3) и E(6;-1) по указанному выше уравнению. (x+8)·2-(y+3)·14 = 0 Это уравнение медианы AE. Площадь треугольника, заданного на плоскости координатами вершин (x1,y1) (x2,y2) (x3,y3) определяется выражением: S = (1/2)·|(x3-x1)·(y2-y1) – (y3-y1)·(x2-x1)| 💡 ВидеоУравнение прямой и треугольник. Задача про высотуСкачать  №942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать  найти уравнение высоты треугольникаСкачать  Вычисление медианы, высоты и угла по координатам вершинСкачать  Даны координаты вершин треугольника АВС.Скачать  №973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать  Уравнения прямой на плоскости | Векторная алгебраСкачать  Аналитическая геометрия, 6 урок, Уравнение прямойСкачать  Математика без Ху!ни. Уравнение плоскости.Скачать  №496. Основание D высоты CD треугольника ABC лежит на стороне АВ, причем AD=BC.Скачать  Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать  Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать  Аналитическая геометрия на плоскости. Решение задачСкачать  Задание 6 ЕГЭ по математике. Урок 26Скачать  Задача 6 №27350 ЕГЭ по математике. Урок 42Скачать  Математика без Ху!ни. Смешанное произведение векторовСкачать  В треугольнике ABC AC = BC = 4 корень из 15, синус BAC = 0,25. Найдите высоту AH.Скачать  №562. В треугольнике ABC сторона АВ равна а, а высота CH равна h. Найдите сторону квадратаСкачать  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||













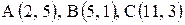 .
. .
. А
А .
.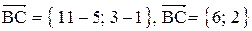 ;
;  .
. ;
; 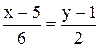 ;
; 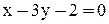 .
. перпендикулярно вектору
перпендикулярно вектору  :
: 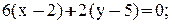
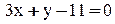 . Длину высоты АК можно найти как расстояние от точки А до прямой ВС:
. Длину высоты АК можно найти как расстояние от точки А до прямой ВС: 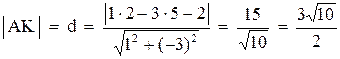 .
. ;
; 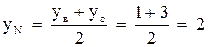 ;
; 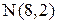 .
. .
. :
: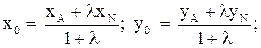
 .
.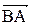 и
и 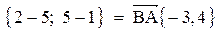 ;
; 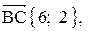
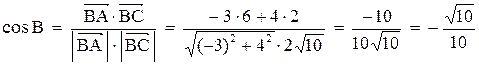 .
.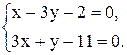 Систему решим по формулам Крамера:
Систему решим по формулам Крамера: 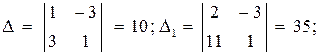
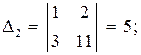
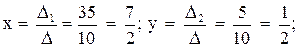
 .
.
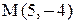 .
.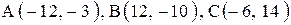 .
. .
. .
. .
. .
. .
. .
. .
.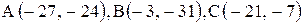 .
.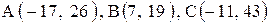 .
.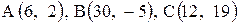 .
. .
. .
.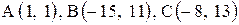 .
.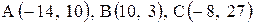 .
. .
.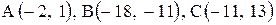 .
.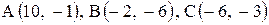 .
.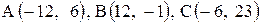 .
. .
.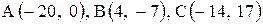 .
.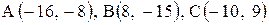 .
.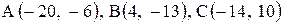 .
.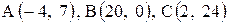 .
. .
.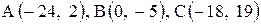 .
.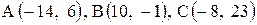 .
.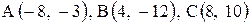 .
.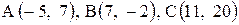 .
.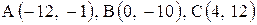 .
. | 8008 –
| 8008 –  или читать все.
или читать все.