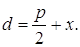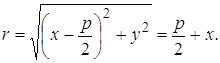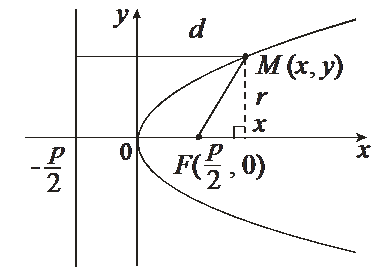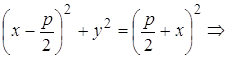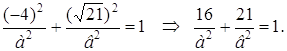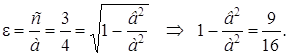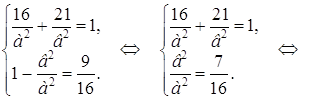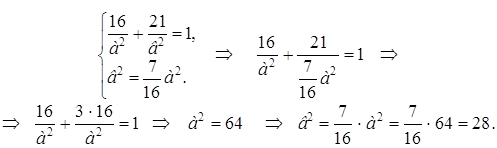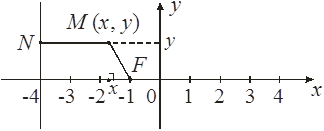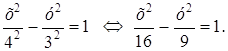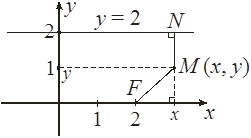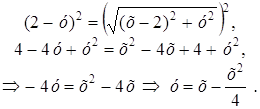Условие
Найти уравнение траектории точки M(x,y) , которая при своем движении все время остается вдвое ближе к точке А(0,1), чем к точке В(-2,0) .
Решение
BM вдвое больше АМ
Возводим в квадрат
(x+2)^2+y^2=4(x^2+(y-1)^2
Упрощаем и получаем о т в е т.
[b]3x^2-4x=3y^2-8y[/b] Это гипербола со смещенным центром.
Парабола
Видео:10.1.04. Уравнение траекторииСкачать

Параболой называется множество точек плоскости, равноудаленных от данной точки F этой плоскости, называемой фокусом параболы, и данной прямой, называемой ее директрисой.
Построим уравнение параболы.
Пусть ось Оx проходит через фокус F параболы и перпендикулярен директрисе, а ось Оу проходит посередине между фокусом и директрисой. Обозначим через p – расстояние между фокусом и директрисой. Тогда 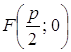
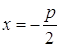
Число p – называется фокальным параметром параболы.
Пусть 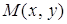

По определению параболы 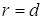
Возведем это уравнение в квадрат
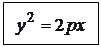
– каноническое уравнение параболы, симметричной относительно оси Оx и проходящей через начало координат.
Точка (0; 0) – вершина параболы.
Если р > 0 (р > 0 ), то парабола (20) расположена правее (левее) оси Оу.
Так как для параболы 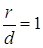
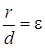
Видео:Траектория и уравнения движения точки. Задача 1Скачать

Заметим, что парабола, симметричная относительно Оу и проходящая через начало координат, определяется уравнением
Фокус этой параболы находится в точке 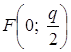

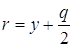
Если q > 0 (q 2 + у 2 – 4х + 6у – 3 = 0.
Выделим полные квадраты в данном уравнении:
х 2 + у 2 – 4х + 6у – 3 = (х 2 – 4х + 4) – 4 + (у 2 + 6у + 9) – 9 – 3 = 0
Þ (х – 2) 2 + (у + 3) 2 = 16.
Учитывая уравнение окружности (1), имеем, что ее центр находится в точке с координатами (2; –3), а радиус равен 4.
Эллипс, симметричный относительно осей координат, фокусы которого находятся на оси Ох, проходит через точку М(–4; 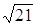
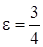
Каноническое уравнение эллипса имеет вид
Так как эллипс проходит через точку М, то ее координаты должны удовлетворять этому уравнению
Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Фокусы находятся на оси Ох, следовательно
Объединив полученные два уравнения в систему, найдем а 2 и в 2 :
Следовательно, уравнение данного эллипса имеет вид:
Фокальные радиусы точки М определим по формулам (8): х = –4, 
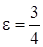
Þ r1 = а + eх = 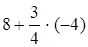
r2 = а – eх = 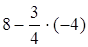
Определить траекторию точки М, которая при своем движении остается вдвое ближе к точке F (–1; 0), чем к прямой х = –4.
Пусть М (х, у). Тогда çMNú = 2 çMFú, çMNú = ç–4 – xú, çMFú= = 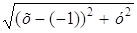
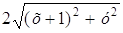
Возведем в квадрат: (4 + х) 2 = 4 ((х + 1) 2 + у 2 ),
Þ 16 + 8х + х 2 = (х 2 + 2х + 1 + у 2 ) · 4 = 4х 2 + 8х + 4 + 4у 2 ,
Þ 3х 2 + 4у 2 = 12 Þ 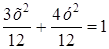

Таким образом, точка М (х, у) движется по эллипсу.
Написать уравнение гиперболы, имеющей вершины в фокусах, а фокусы – в вершинах эллипса 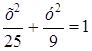
Видео:Естественный способ задания движенияСкачать

Из уравнения данного эллипса имеем: а = 5; в = 3, а > в.
Следовательно, 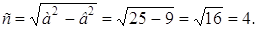
Так как фокусы эллипса находятся на оси Ох (а > в), то вершины (±5; 0) будут фокусами гиперболы. Каноническое уравнение гиперболы, имеющей фокусы на оси Ох, имеет вид (13)
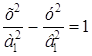
причем F1(–5; 0), F2(5; 0) – фокусы данной гиперболы, т. е. с1 = 5. Найдем а1 и в1.
Так как вершины данной гиперболы находятся в фокусах эллипса, то а1 = с = 4. Следовательно:
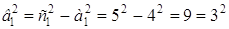
Таким образом, уравнение гиперболы имеет вид
Составить уравнение геометрического места точек, одинаково удаленных от точки F(2; 0) и от прямой у = 2. Найти вершину параболы, точки пересечения ее с осью Ох.
Пусть точка М (х, у) – принадлежит данному множеству точек.
Следовательно çFMú = çNMú , çFMú == 
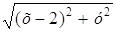
Видео:Способы описания движения. Траектория. Путь. ПеремещениеСкачать

Возведем в квадрат:
– парабола, ветви которой направлены вниз.
Найдем точки пересечения данной параболы с осью Ох.
у = 0 Þ 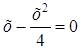
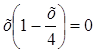
Т. е. это будут точки (0; 0); (4; 0).
Þ Вершина параболы будет в точке с абсциссой х = 2 Þ 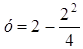
Вершиной параболы будет точка (2; 1).
На параболе у 2 = 6х найти точку, фокальный радиус которой равен 4,5.
Так как у 2 = 2рх Þ 2р = 6, р = 3. 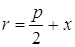
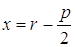
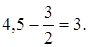
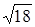
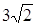
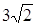
1. Гусак А. А. Аналитическая геометрия и линейная алгебра.– Мн.: Тетрасистемс, 1998.
Видео:Курс «Баллистика и орбитальная механика» — «Уравнения движения тела в центральном поле»Скачать

2. Овсеец М. И., Светлая Е. М. Сборник задач по высшей математике. Учебное издание.– Мн.: ЧИУиП, 2006.– 67 с.
🌟 Видео
Частное положение точек. Точки принадлежащие к плоскостям проекции.Скачать

ФИЗИКА 10 класс : Механическое движение | Материальная точка, траектория, перемещение.Скачать

Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Составляем уравнение прямой по точкамСкачать

Тема: Путь и перемещениеСкачать

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Путь. Перемещение. Траектория.Скачать

Урок 37. Движение тела, брошенного под углом к горизонту (начало)Скачать

Основное уравнение динамики вращательного движения. 10 класс.Скачать

Поступательное и вращательное движенияСкачать

Кинематика точки. Три способа задания движения. Скорость, ускорениеСкачать

Задача 8. Написать уравнение плоскости, проходящей через точку перпендикулярно вектору.Скачать

Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать

Естественный способ задания движенияСкачать