Написать уравнение соприкасающейся плоскости в произвольной точке

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе

Видео:Дифференциальная геометрия | соприкасающаяся плоскостьСкачать

Краткие теоретические сведения

Кривая в пространстве

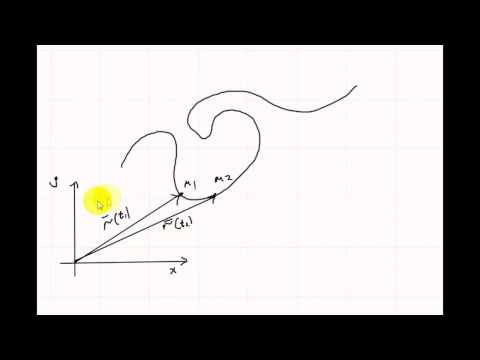
Рассмотрим в пространстве гладкую кривую $gamma$.

Пусть точка $M$ принадлежит данной кривой и отвечает значению параметра $t=t_0$. Тогда радиус-вектор и координаты данной точки равны:

begin vec=vec(t_0), quad x_0=x(t_0),, y_0=y(t_0), , z_0=z(t_0). end

Пусть в точке $M$ $ vec(t_0)neqvec$, то есть $M$ не является особой точкой.

Касательная к кривой

Касательная к кривой, проведенная в точке $M$, имеет направляющий вектор коллинеарный вектору $vec(t_0)$.

Пусть $vec$ — радиус-вектор произвольной точки касательной, тогда уравнение этой касательной имеет вид

Здесь $lambdain(-infty,+infty)$ — параметр, определяющий положение точки на касательной (то есть разным значениям $lambda$ будут соответствовать разные значения $vec$).

Если $vec=$, $M = (x(t_0), y(t_0), z(t_0))$, то можно записать уравнение касательной в каноническом виде:

Нормальная плоскость

Плоскость, проходящую через данную точку $M$ кривой $gamma$ перпендикулярно касательной в этой точке, называют нормальной плоскостью.

Пусть $vec$ — радиус-вектор произвольной точки нормальной плоскости, тогда ее уравнение можно записать в векторном виде через скалярное произведение векторов $vec-vec(t_0)$ и $vec(t_0)$:

Если расписать покоординатно, то получим следующее уравнение:

begin x'(t_0)cdot(X-x(t_0))+y'(t_0)cdot(Y-y(t_0))+z'(t_0)cdot(Z-z(t_0))=0. end

Соприкасающаяся плоскость

Плоскость, проходящую через заданную точку $M$ кривой $gamma$ параллельно векторам $vec(t_0)$, $vec(t_0)$, когда они неколлинеарны, называют соприкасающейся плоскостью кривой.

Если $vec$ — радиус-вектор произвольной точки соприкасающейся плоскости, то ее уравнение можно записать через смешанной произведение трех компланарных векторов $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)$:

Зная координаты точки и векторов, определяющих плоскость, запишем смешанное произведение через определитель. Получим следующее уравнение соприкасающейся плоскости:

begin left| begin X-x(t_0) & Y-y(t_0) & Z-z(t_0) \ x'(t_0) & y'(t_0) & z'(t_0)\ x»(t_0) & y»(t_0) & z»(t_0) \ end right|=0 end

Бинормаль и главная нормаль

Прямая, проходящая через точку $M$ кривой $gamma$ перпендикулярно касательной к кривой в этой точке, называется нормалью.

Таких кривых можно провести бесконечно много, все они образуют нормальную плоскость. Мы выделим среди нормалей две — бинормаль и главную нормаль.

Нормаль, перпендикулярную соприкасающейся плоскости, называют бинормалью.

Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью.

Из определения бинормали (перпендикулярна касательной и перпендикулярна соприкасающейся плоскости) следует, что в качестве ее направляющего вектора мы можем взять векторное произведение $ vec(t_0)timesvec(t_0)$, тогда ее уравнение можно записать в виде:

Как и раньше, $vec$ — радиус-вектор произвольной точки бинормали. Каноническое уравнение прямой:

Из определения главной нормали (перпендикулярна касательной и перпендикулярна бинормали) следует, что в качестве ее направляющего вектора можно взять векторное произведение $vec(t_0) timesleft[vec(t_0),vec(t_0)right]$:

Уравнение в каноническом виде распишите самостоятельно.

Спрямляющая плоскость

Плоскость, проходящую через заданную точку $M$ кривой $gamma$ перпендикулярно главной нормали, называют спрямляющей плоскостью.

Другое определение: Плоскость, определяемую касательной к кривой и бинормалью в той же точке, называют спрямляющей плоскостью.

Второе определение позволяет записать уравнение спрямляющей плоскости через смешанное произведение трех компланарных векторов, определяющих эту плоскость $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)timesvec(t_0)$: begin left(vec-vec(t_0),, vec(t_0),, vec(t_0)timesvec(t_0)right)=0. end Зная координаты соответствующих векторов, можно легко записать это смешанное произведение через определитель, раскрыв который, вы получите общее уравнение спрямляющей плоскости.

Репер Френе

Орт (то есть единичный вектор) касательной обозначим: $$ vec=frac<vec(t_0)><|vec(t_0)|>. $$ Орт бинормали: $$ vec=frac<vec(t_0)timesvec(t_0)><|vec(t_0)timesvec(t_0)|>. $$ Орт главной нормали: $$ vec=frac<vec(t_0) times[vec(t_0),,vec(t_0)]><|vec(t_0) times [vec(t_0),,vec(t_0)]|>. $$

Правая тройка векторов $vec$, $vec$, $vec$ называется репером Френе.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Решение задач

Задача 1

Кривая $gamma$ задана параметрически:

Точка $M$, принадлежащая кривой, соответствует значению параметра $t=0$. Записать уравнения касательной, бинормали, главной нормали, нормальной плоскости, соприкасающейся плоскости и спрямляющей плоскости, проведенных к данной кривой в точке $M$. Записать векторы репера Френе.

Решение задачи 1

Задачу можно решать разными способами, точнее в разном порядке находить уравнения прямых и плоскостей.

Начнем с производных.

begin 1cdot X+0cdot Y+1cdot (Z-1)=0,, Rightarrow ,, X+Z=1. end

begin left| begin X-0 & Y-0 & Z-1 \ 1 & 0 & 1\ 0 & 2 & 1 \ end right|=0 end Раскрываем определитель, получаем уравнение: begin -2X-Y+2Z-2=0 end

begin 1cdot X-4cdot Y-1cdot (Z-1)=0,, Rightarrow ,, X-4Y-Z+1=0. end

Поскольку направляющий вектор главной нормали у нас был найден как векторное произведение направляющих векторов касательной и бинормали, тройка $vec$, $vec$, $vec$ не будет правой (по определению векторного произведения вектор $vectimesvec$ направлен так, что тройка векторов $vec$, $vec$, $vec=vectimesvec$

— правая). Изменим направление одного из векторов. Например, пусть

Теперь тройка $vec$, $vec$, $vec<tilde>$ образует репер Френе для кривой $gamma$ в точке $M$.

Задача 2

Написать уравнение соприкасающейся плоскости к кривой $$ x=t,,, y=frac,,, z=frac, $$ проходящей через точку $N(0,0,9)$.

Решение задачи 2

Нетрудно заметить, что точка $N$ не принадлежит заданной кривой $gamma$. Следовательно соприкасающаяся плоскость проведена в какой-то точке $M(t=t_0)ingamma$, но при этом плоскость проходит через заданную точку $N(0,0,9)$.

Найдем значение параметра $t_0$.

Для этого запишем уравнение соприкасающейся плоскости, проведенной в произвольной точке $M(t=t_0)$. И учтем, что координаты $N$ должны удовлетворять полученному уравнению.

Соприкасающаяся плоскость определяется векторами $vec(t_0)$, $vec(t_0)$, поэтому записываем определитель begin left| begin X-t_0 & Y-t_0^2/2 & Z-t_0^3/3 \ &&\ 1 & t_0 & t^2_0 \ &&\ 0 & 1 & 2t_0 end right|=0 quad Rightarrow end

begin (X-t_0)cdot t_0^2 — (Y-t_0^2/2)cdot 2t_0 + (Z-t_0^3/3)=0. end Подставляем вместо $X$, $Y$, $Z$ координаты точки $N$: $X=0$, $Y=0$, $Z=9$, упрощаем и получаем уравнение относительно $t_0$: begin 9-t_0^3/3=0 quad Rightarrow quad t_0=3. end Подставив найденное $t_0$ в записанное ранее уравнение, запишем искомое уравнение соприкасающейся плоскости: $$ 9X-6Y+Z-9=0. $$

Задача 3

Через точку $Pleft(-frac45,1,2right)$ провести плоскость, являющуюся спрямляющей для кривой: $$ x=t^2,,, y=1+t,,, z=2t. $$

Решение задачи 3

Как и в предыдущей задаче нам неизвестны координаты точки, в которой проведена спрямляющая плоскость к заданной кривой. Найдем их.

Спрямляющая плоскость определяется касательной и бинормалью, то есть векторами $vec(t_0)$ и $vec(t_0)timesvec(t_0)$.

Записываем уравнение спрямляющей плоскости: begin left| begin X-t_0^2 & Y-1-t_0 & Z-2t_0 \ 2t_0 & 1 & 2\ 0 & 4 & -2 end right|= 0 end

Раскрываем определитель. Подставляем в уравнение координаты точки $P$: $X=-4/5$, $Y=1$, $Z=2$. Упрощаем и получаем уравнение для нахождения $t_0$: begin 5t_0^2-8t_0-4=0 ,, Rightarrow ,, t_=2,, t_=-frac25. end

Уравнения соприкасающихся плоскостей к заданной кривой, проходящих через $P$, принимают вид: begin & 5X-4Y-8Z+24=0,\ & 25X+4Y+8Z=0. end

Видео:Дифференциальная геометрия | спрямляющая плоскостьСкачать

Соприкасающаяся плоскость

Плоскость, проходящую через касательную и главную нормаль в данной точке кривой, называют соприкасающейся плоскостью.

Отсюда и из определения главной нормали следует, что соприкасающаяся плоскость определена для точек кривой, в которых кривизна (kneq 0).

Если гладкая кривая (Gamma=<textbf=textbf(t),;alphaleq tleqbeta>) дважды дифференцируема и ее кривизна в точке (M_=M(t_)) не равна нулю, то уравнение соприкасающейся плоскости (Q) в точке (M_) имеет вид
$$
(r-r(t_0),r'(t_0),r″(t_0))=0.label
$$

(circ) Если (s=s(t)) — переменная длина дуги кривой (Gamma), то дифференцируя (r(t)) как сложную функцию и используя эту и эту формулы, получаем
$$
textbf_’=textbf_’s_’=s_’tau,quad textbf_″=frac

(s_’tau)=s_″tau+s_’tau_’s_’=s_″tau+(s_’)^knu,nonumber
$$
где индексы указывают, по каким переменным производится дифференцирование. Отсюда следует, что векторы (textbf_’) и (textbf_″) параллельны плоскости (Q). По условию (kneq 0), и поэтому ([textbf_’,textbf_″]neq 0). Следовательно, векторы (textbf_’) и (textbf_″) не коллинеарны.

Рис. 22.8

Так как векторы (textbf-textbf(t_), textbf'(t_)=textbf_'(t_), textbf″(t_0)=textbf_″(t_)) параллельны плоскости (Q) (рис. 22.8), то их смешанное произведение равно нулю, то есть во всех точках плоскости (Q) (и только в этих точках) должно выполняться условие eqref. (bullet)

Запишем уравнение eqref в координатной форме:
$$
beginx-x(t_0)&y-y(t_0)&z-z(t_0)\x'(t_0)&y'(t_0)&z'(t_0)\x″(t_0)&y″(t_0)&z″(t_0)end=0nonumber
$$

Видео:Задача 8. Написать уравнение плоскости, проходящей через точку перпендикулярно вектору.Скачать

Написать уравнение соприкасающейся плоскости в произвольной точке

Пространственные кривые. Задание пространственной кривой. Регулярное задание кривой. Регулярная кривая. Неявное задание пространственной кривой. Касательная к пространственной кривой. Единичный вектор касательной. Бинормаль и главная нормаль и их единичные векторы. Нормальная, соприкасающаяся и спрямляющая плоскости. Ускорение при криволинейном движении и векторы сопровождающего трехгранника. Кривизна пространственной кривой. Теорема о прямой. Кручение пространственной кривой. Теорема о плоской кривой. Формулы Френе. Естественный параметр и натуральные уравнения кривой.

Основные определения, результаты, комментарии

Элементарной кривой в пространстве называется образ открытого интервала при его гомеоморфизме в евклидово трехмерное пространство.

Общей кривой на плоскости называется подмножество евклидова пространства, локально гомеоморфное прямой.

Как и в случае плоских кривых, всякая общая кривая допускает покрытие элементарными кривыми.

Кривая задана неявным способом

если координаты каждой точки кривой удовлетворяют обоим уравнениям .

Наиболее удобны и наиболее часто используются векторно-параметрическое представление

и координатно-параметрическое представление

отличающиеся лишь формой записи.

Определение регулярности параметрического представления пространственной кривой полностью аналогично плоскому случаю.

Неявное задание (5) кривой регулярно в точке , если матрица частных производных

имеет в этой точке ранг 2.

Понятия длины кривой, ее естественной параметризации, а также определение касательной полностью аналогичны тем же понятиям для плоских кривых. Направляющий вектор касательной - это, по-прежнему, производная , имеющая физический смысл скорости, если параметрическое представление кривой интерпретировать как кинематическое описание движения точки.

Нормальная плоскость кривой в точке - это плоскость, проходящая через точку ортогонально касательной.

Соприкасающейся плоскостью кривой в ее точке (рис. 17) называется содержащая эту точку плоскость , удовлетворяющая соотношению

где - точка, принадлежащая элементарной окрестности точки .

Спрямляющей плоскостью кривой в ее точке называется содержащая эту точку плоскость, ортогональная нормальной и соприкасающейся плоскостям в этой точке.

Прямые, ортогональные соприкасающейся и спрямляющей плоскостям в точке , называются соответственно бинормалью и главной нормалью кривой в точке .

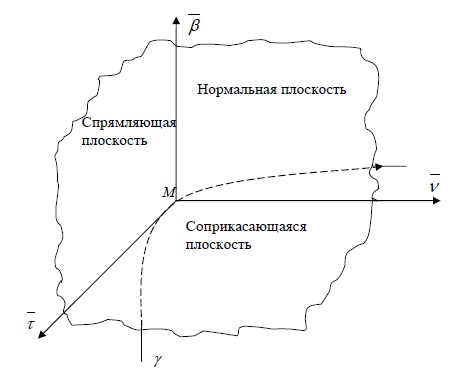
Нормальная, соприкасающаяся и спрямляющая плоскости образуют сопровождающий трехгранник кривой , или трехгранник Френе , в точке , и называются его гранями . Касательная, бинормаль и главная нормаль называются ребрами сопровождающего трехгранника (рис. 18).

Уравнения элементов сопровождающего трехгранника вычисляются по следующим правилам:

Касательная	Нормальная плоскость
Бинормаль	Соприкасающаяся плоскость
Главная нормаль	Спрямляющая плоскость

Единичные векторы

касательной

главной нормали

бинормали

Если параметризация естественная , то вектор главной нормали может быть вычислен по формуле .

Вектор ускорения может быть разложен в сумму двух составляющих: нормальной (ортогональной вектору скорости) и тангенциальной (параллельной вектору скорости). При этом нормальная составляющая ускорения сонаправлена единичному вектору главной нормали.

Пусть и - две различные точки кривой , соответствующие значениям и естественного параметра. Тогда - длина дуги кривой, заключенной между точками и . Пусть - величина угла, образуемого касательной к кривой в точке по отношению к касательной в точке . Кривизна кривой в ее точке - это предел

В отличие от кривизны плоской кривой, кривизна пространственной кривой всегда положительна . Кривизна пространственной кривой в регулярной точке может быть вычислена по формулам:

если параметризация естественная.

Пусть и - две различные точки кривой , соответствующие значениям естественного параметра и соответственно, и - единичные векторы бинормалей в этих точках (рис. 19).

Обозначим за величину угла между ними. Очевидно, этот угол равен углу, образованному соприкасающимися плоскостями в точках и .

Абсолютным кручением кривой в точке называют величину

Кручение кривой определяется в соответствии со следующим правилом: если при движении вдоль кривой по направлению возрастания параметра вектор бинормали поворачивается в сторону, указываемую вектором , в противном случае. Наглядно это означает, что кривая с положительным кручением "закручена" по правилу правого винта.

Кручение кривой в точке, соответствующей значению параметра , может быть вычислено по следующим формулам:

Для производных векторов , по естественному параметру справедливы формулы Френе :

Уравнения и называются натуральными уравнениями кривой. По натуральным уравнениям вид кривой может быть восстановлен с точностью до перемещения. В большинстве случаев решение такой задачи оказывается очень сложным.

1. Для данных представлений кривых укажите область допустимых значений параметра и область значений параметра, в которой задание кривой регулярно.
1)
2)
3)
4) .

2. Кривая задана неявными уравнениями. Изобразите на рисунке вид кривой. Постройте какое-нибудь параметрическое представления этой кривой. Укажите область допустимого изменения параметра и область регулярности параметризации.
1)
2) R,;; y>0;$ --> R,;; y>0;$">
3)

3. Кривая Вивиани образована пересечением сферы радиуса и цилиндра радиуса , проходящего через центр сферы. Постройте параметрическое представление кривой Вивиани.

4. Винтовая линия. Окружность радиуса движется так, что ее центр перемещается вдоль оси , плоскость ортогональна оси . По окружности равномерно движется точка. В начальный момент времени точка имеет координаты . Составьте параметрические уравнения кривой, описываемой данной точкой.

5. Кривая задана пересечением цилиндрических поверхностей и Постройте параметрическое представление кривой , не содержащее радикалов, и дайте ее изображение.

6. Покажите, что линия

принадлежит сфере и является линией пересечения параболического и кругового цилиндров.

7. Найдите длину дуги линии

между плоскостями и .

8. Покажите, что кривая замкнута и имеет длину .

9. Запишите в естественной параметризации
a) винтовую линию ;
б) гиперболическую винтовую линию .

10. Кривая задана параметрически: 0. end -->

Напишите уравнения
а) касательной и нормальной плоскости в точке (1/4; 1/3; 1/2);
б) касательной, параллельной плоскости .

11. Найдите линию, по которой касательные к линии

Сферической индикатрисой данной кривой называется геометрическое место концов единичных касательных векторов, отложенных от начала координат.

12. Дана винтовая линия

a) Напишите уравнение семейства касательных этой кривой;
б) убедитесь в том, что все касательные к винтовой линии образуют с плоскостью один и тот же угол;
в) составьте уравнение кривой, образуемой точками пересечения касательных с плоскостью ;
г) найдите сферическую индикатрису винтовой линии.

13. Докажите, что все нормальные плоскости кривой Вивиани (задача 3) проходят через начало координат.

14. Составьте уравнения бинормали и главной нормали кривой в указанной точке:
1)
2)
3) ;
4)

15. Найдите точки на кривой

в которых бинормаль параллельна плоскости .

16. Материальная точка движется в пространстве по закону

Укажите моменты времени, в которые
а) ее скорость равна нулю, и сравните их со значениями параметра , при которых параметризация траектории нерегулярна;
б) нормальное ускорение точки ортогонально .

17. Составьте уравнения ребер и граней сопровождающего трехгранника данной кривой в указанной точке
1)
2)
3)
4)

18. Для данной кривой вычислите кривизну в данной точке сначала по готовой формуле, а затем по следующему плану: 1) составьте уравнение поля единичных касательных векторов данной кривой; 2) вычислите абсолютную величину производной этого поля по естественному параметру. Результаты сравните.
1) 0,;; bne 0, ;; t_0=pi/2$ --> 0,;; bne 0, ;; t_0=pi/2$">
2)

19. Для кривых задачи 18 вычислите абсолютное кручение в данной точке сначала по готовой формуле, а затем по следующему плану: 1) составьте уравнение поля единичных векторов бинормали данной кривой; 2) вычислите абсолютную величину производной этого поля по естественному параметру. Результаты сравните.

20. Вычислите кривизну и кручение данной кривой произвольной регулярной точке:
1) 0,;; bne 0$ --> 0,;; bne 0$">;
2)
3)
4) .

21. Найдите точки распрямления следующих кривых:
1)
2)
3) .

22. Найдите точки уплощения и дуги, на которых кручение сохраняет свой знак, у следующих кривых:
1)
2)

23. Напишите натуральные уравнения, которым удовлетворяют следующие кривые:
1) 0,;; bne 0$ --> 0,;; bne 0$">;
2)

24. Найдите точки на кривой

в которых кривизна принимает локально минимальное значение.

25. Найдите точки на кривой

в которых радиус кривизны достигает локального максимума.

26. Докажите, что следующие кривые плоские, и составьте уравнения плоскостей, в которых они расположены:

27. Найдите такую функцию , чтобы кривая

была плоской. Решите задачу двумя способами: 1) используя условие плоскости и 2) используя тот факт, что искомая кривая принадлежит круговому цилиндру (составьте его уравнение!). Результаты сравните.

28. Докажите, что если все соприкасающиеся плоскости линии проходят через неподвижную точку , то линия плоская.

29. Докажите, что если соприкасающиеся плоскости линии (отличной от прямой) параллельны некоторому вектору , то линия плоская.

30. Докажите, что если все нормальные плоскости линии параллельны некоторому вектору , то линия или прямая, или плоская.

💥 Видео

Дифференциальная геометрия | касательная плоскость | 3Скачать

Математика Без Ху!ни. Касательная плоскость и нормаль к поверхности.Скачать

Дифференциальная геометрия | нормальная плоскостьСкачать

Мохов О. И. - Дифференциальная геометрия - Плоские кривыеСкачать

Мохов О. И. - Дифференциальная геометрия - Эволюта, эвольвента; пространственные кривыеСкачать

Дифференциальная геометрия | соприкасающаяся окружность | произвольная параметризация | 1Скачать

Дынников И. А. - Классическая дифференциальная геометрия - Теорема КлероСкачать

Дифференциальная геометрия | соприкасающаяся окружность | натуральная параметризацияСкачать

Частное положение точек. Точки принадлежащие к плоскостям проекции.Скачать

Дифференциальная геометрия | касательная плоскость | 2Скачать

Дифференциальная геометрия | натуральный параметрСкачать

Дифференциальная геометрия | нормаль плоской кривой для произвольной параметризацииСкачать

Дынников И. А. - Классическая дифференциальная геометрия - Касательные к кривойСкачать

Как строить сеченияСкачать

Дифференциальная геометрия | плоская кривая и её параметризацияСкачать